NCERT Solutions Class 12 Maths Chapter-9 (Determinants)Exercise 9.3

NCERT Solutions Class 12 Maths from class 12th Students will get the answers of Chapter-9 (Determinants)Exercise 9.3 This chapter will help you to learn the basics and you should expect at least one question in your exam from this chapter.
We have given the answers of all the questions of NCERT Board Mathematics Textbook in very easy language, which will be very easy for the students to understand and remember so that you can pass with good marks in your examination.

Exercise 9.3

Q1. $\frac{x}{a} + \frac{y}{b} = 1$

Answer. $\begin{array}{l} \frac{x}{a} + \frac{y}{b} = 1 \\ Differentiating both sides of the given equation with respect to x, we get: \\ \frac{1}{a} + \frac{1}{b} \frac{d y}{d x} = 0 \\ \Rightarrow \frac{1}{a} + \frac{1}{b} y^{'} = 0 \end{array}$ $\begin{array}{l} Again, differentiating both sides with respect to x, we get: \\ 0 + \frac{1}{b} y^{''} = 0 \\ \Rightarrow \frac{1}{b} y^{''} = 0 \\ \Rightarrow \frac{1}{b} y^{''} = 0 \\ \Rightarrow y^{''} = 0 \\ y^{''} = 0 \end{array}$ $\begin{array}{l} Hence, the required differential equation of the given curve is \\ y^{''} = 0 \end{array}$

Q2. $y^{2} = a (b^{2} - x^{2})$

Answer. $\begin{array}{l} y^{2} = a (b^{2} - x^{2}) \\ Differentiating both sides with respect to x, we get: \\ 2 y \frac{d y}{d x} = a (- 2 x) \\ \Rightarrow 2 y y^{'} = - 2 a x \\ \Rightarrow y y^{'} = - a x . . . (i) \\ Again, differentiating both sides with respect to x, we get: \end{array}$ $\begin{array}{l} y^{'} \cdot y^{'} + y y^{''} = - a \\ \Rightarrow {(y^{'})}^{2} + y y^{'} = - a . . . (i i) \\ Dividing equation (i i) by equation (i), we get: \\ \frac{{(y^{'})}^{2} + y y^{*}}{y y^{'}} = \frac{- a}{- a x} \\ \Rightarrow x y y^{''} + x {(y^{'})}^{2} - y y^{'} = 0 \end{array}$ This is the required differential equation of the given curve.

Q3. $y = a e^{3 x} + b e^{- 2 x}$

Answer.

\begin{array}{l} y = a e^{3 x} + b e^{- 2 x} . . . (i) \\ Differentiating both sides with respect to x, we get: \\ y^{'} = 3 a e^{3 x} - 2 b e^{- 2 x} . . . (i i) \\ Again, differentiating both sides with respect to x, we get: \\ y^{'} = 9 a e^{3 x} + 4 b e^{- 2 x} . . . (i i i) \\ Multiplying equation (i) with (i i) and then adding it to equation (i i), we get: \end{array}

\begin{array}{l} (2 a e^{3 x} + 2 b e^{- 2 x}) + (3 a e^{3 x} - 2 b c^{- 2 x}) = 2 y + y^{'} \\ \Rightarrow 5 a e^{3 x} = 2 y + y^{'} \\ \Rightarrow a e^{3 x} = \frac{2 y + y^{'}}{5} \\ Now, multipling equation (i) with (i i i) and subtracting equation \\ (i i) from it, we get: \end{array}

\begin{array}{l} (3 a e^{3 x} + 3 b e^{- 2 x}) - (3 a e^{3 x} - 2 b e^{- 2 x}) = 3 y - y^{'} \\ \Rightarrow 5 b e^{- 2 x} = 3 y - y^{'} \\ \Rightarrow b e^{- 2 x} = \frac{3 y - y^{'}}{5} \\ Substituting the values of a e^{2 x} and b e^{- 2 x} in equation (i i i), we get: \end{array}

\begin{array}{l} y^{''} = 9 \cdot \frac{(2 y + y^{'})}{5} + 4 \frac{(3 y - y^{'})}{5} \\ \Rightarrow y^{''} = \frac{18 y + 9 y^{'}}{5} + 4 \frac{12 y - 4 y^{'}}{5} \\ \Rightarrow y^{''} = \frac{30 y + 5 y^{'}}{5} \\ \Rightarrow y^{''} = \frac{5 y + y^{'}}{5} \\ \Rightarrow y^{''} - y^{'} - 6 y = 0 \end{array}

This is the required differential equation of the given curve.

Q4. $y = e^{2 x} (a + b x)$

Answer.

\begin{array}{l} y = e^{2 x} (a + b x) . . . (i) \\ Differentiating both sides with respect to x, we get: \\ y^{'} = 2 e^{2 x} (a + b x) + e^{2 x} \cdot b \\ \Rightarrow y^{'} = e^{2 x} (2 a + 2 b x + b) . . . (i i) \end{array}

\begin{array}{l} Multiplying equation (i) with equation (i i) and then subtracting it from equation (i i), we \\ get: \\ y^{'} - 2 y = e^{2 x} (2 a + 2 b x + b) - e^{2 x} (2 a + 2 b x) \\ \Rightarrow y^{'} - 2 = b e^{2 x} . . . (i i i) \\ Differentiating both sides with respect to x, we get: \\ y^{'} k - 2 y^{'} = 2 b e^{2 x} . . . (i v) \end{array}

\begin{array}{l} Dividing equation (i v) by equation (i i i), we get: \\ \frac{y^{'} - 2 y^{'}}{y^{'} - 2 y} = 2 \\ \Rightarrow y^{'} - 2 y^{'} = 2 y^{'} - 4 y \\ \Rightarrow y^{''} - 4 y^{'} + 4 y = 0 \end{array}

This is the required differential equation of the given curve.

Q5. $y = e^{x} (a \cos x + b \sin x)$

Answer. $\begin{array}{l} y = e^{x} (a \cos x + b \sin x) . . . (i) \\ Differentiating both sides with respect to x, we get: \\ y^{'} = e^{x} (a \cos x + b \sin x) + e^{x} (- a \sin x + b \cos x) \\ \Rightarrow y^{'} = e^{x} [(a + b) \cos x - (a - b) \sin x] . . . (i i) \end{array}$ $\begin{array}{l} Again, differentiating with respect to x, we get: \\ y^{''} = e^{r} [(a + b) \cos x - (a - b) \sin x] + e^{x} [- (a + b) \sin x - (a - b) \cos x] \\ y^{''} = e^{x} [2 b \cos x - 2 a \sin x] \\ y^{''} = 2 e^{x} (b \cos x - a \sin x) \\ \Rightarrow \frac{y^{'}}{2} = e^{x} (b \cos x - a \sin x) . . . (i i i) \\ Adding equations (i) and (i i i), we get: \end{array}$ $\begin{array}{l} y + \frac{y^{'}}{2} = e^{x} [(a + b) \cos x - (a - b) \sin x] \\ \Rightarrow y + \frac{y^{''}}{2} = y^{'} \\ \Rightarrow 2 y + y^{''} \\ \Rightarrow y^{''} - 2 y^{'} + 2 y = 0 \\ \Rightarrow y^{''} - 2 y^{'} + 2 y = 0 \\ This is the required differential equation of the given curve. \end{array}$

Q6. Form the differential equation of the family of circles touching the y-axis at the origin.

Answer. The centre of the circle touching the y-axis at origin lies on the x-axis. Let (a, 0) be the centre of the circle. Since it touches the y-axis at origin, its radius is a. Now, the equation of the circle with centre (a, 0) and radius (a) is

\begin{array}{l} (x - a)^{2} + y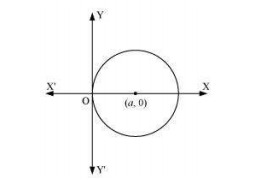^{2} = a^{2} \\ \Rightarrow x^{2} + y^{2} = 2 a x . . . (i) \end{array}

\begin{array}{l} Differentiating equation (i) with respect to x, we get: \\ 2 x + 2 y y^{'} = 2 a \\ \Rightarrow x + y y^{'} = a \\ Now, on substituting the value of a in equation (i), we get: \\ x^{2} + y^{2} = 2 (x + y y^{'}) x \\ \Rightarrow x^{2} + y^{2} = 2 x^{2} + 2 x y y^{'} \\ \Rightarrow 2 x y y^{'} + x^{2} = y^{2} \end{array}

This is the required differential equation.

Q7. Form the differential equation of the family of parabolas having vertex at origin and axis along positive y-axis.

Answer. $\begin{array}{l} The equation of the parabola having the vertex at origin and the axis along the positive \\ y -axis is: \\ x^{2} = 4 a y . . . (i) 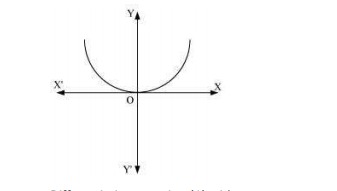\end{array}$ Solutions Class 12 maths Chapter-9 (Determinants) Exercise 9.3 $\begin{array}{l} Differentiating equation (i) with respect to x, we get: \\ 2 x = 4 a y^{'} . . . (i i) \\ Dividing equation (i i) by equation (i), we get: \\ \frac{2 x}{x^{2}} = \frac{4 a y^{'}}{4 a y} \\ \Rightarrow \frac{2}{x} = \frac{y^{'}}{y} \\ \Rightarrow x y^{'} = 2 y \\ \Rightarrow x y^{'} - 2 y = 0 \end{array}$ This is the required differential equation.

Q8. Form the differential equation of the family of ellipses having foci on y-axis and centre at origin.

Answer.

\begin{array}{l} The equation of the family of ellipses having foci on the y -axis and the centre at origin is \\ as follows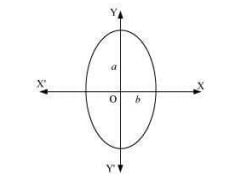: \\ \frac{x^{2}}{b^{2}} + \frac{y^{2}}{a^{2}} = 1 . . . (i) \end{array}

\begin{array}{l} Differentiating equation (i) with respect to x, we get: \\ \frac{2 x}{b^{2}} + \frac{2 y y^{'}}{b^{2}} = 0 \\ \Rightarrow \frac{x}{b^{2}} + \frac{y y^{'}}{a^{2}} = 0 . . . (i i) \\ Again, differentiating with respect to x, we get: \end{array}

\begin{array}{l} \frac{1}{b^{2}} + \frac{y^{'} y^{'} + y . y^{*}}{a^{2}} = 0 \\ \Rightarrow \frac{1}{b^{2}} + \frac{1}{a^{2}} (y^{' 2} + y y^{''}) = 0 \\ \Rightarrow \frac{1}{b^{2}} = - \frac{1}{a^{2}} (y^{2} + y y^{''}) \\ Substituting this value in equation (i i), we get: \end{array}

\begin{array}{l} x [- \frac{1}{a^{2}} ({(y^{'})}^{2} + y y^{'})] + \frac{y y^{'}}{a^{2}} = 0 \\ \Rightarrow - x {(y^{'})}^{2} - x y y^{''} + y y^{'} = 0 \\ \Rightarrow x y y^{''} + x {(y^{'})}^{2} - y y^{'} = 0 \\ This is the required differential equation. \end{array}

Q9. Form the differential equation of the family of hyperbolas having foci on x-axis and centre at origin.

Answer. $\begin{array}{l} The equation of the family of hyperbolas with the centre at origin and foci along the x - \\ axis is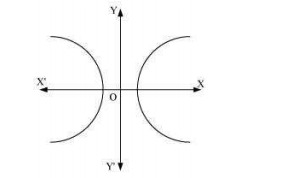: \\ \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 . . . (i) \end{array}$ Solutions Class 12 maths Chapter-9 (Determinants) Exercise 9.3 $\begin{array}{l} Differentiating both sides of equation (i) with respect to x, we get: \\ \frac{2 x}{a^{2}} - \frac{2 y y^{'}}{b^{2}} = 0 \\ \Rightarrow \frac{x}{a^{2}} - \frac{y y^{'}}{b^{2}} = 0 . . . (i i) \end{array}$ $\begin{array}{l} Again, differentiating both sides with respect to x, we get: \\ \frac{1}{a^{2}} - \frac{y^{'} \cdot y^{'} + y y^{''}}{b^{2}} = 0 \\ \Rightarrow \frac{1}{a^{2}} = \frac{1}{b^{2}} ({(y^{'})}^{2} + y y^{''}) \\ Substituting the value of a^{2} in equation (i i), we get: \end{array}$ $\begin{aligned} \frac{x}{b^{2}} ({(y^{'})}^{2} + y y^{'}) - \frac{y y^{'}}{b^{2}} = 0 \\ \Rightarrow x {(y^{'})}^{2} + x y y^{''} - y y^{'} = 0 \\ \Rightarrow x y y^{''} + x {(y^{'})}^{2} - y y^{'} = 0 \end{aligned}$ This is the required differential equation.

Q10. Form the differential equation of the family of circles having centre on y-axis and radius 3 units.

Answer. Let the centre of the circle on y-axis be (0, b). The differential equation of the family of circles with centre at (0, b) and radius 3 is as follows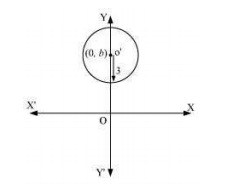: $\begin{array}{l} x^{2} + (y - b)^{2} = 3^{2} \\ \Rightarrow x^{2} + (y - b)^{2} = 9 . . . (i) \end{array}$ Solutions Class 12 maths Chapter-9 (Determinants) Exercise 9.3 $\begin{array}{l} Differentiating equation (i) with respect to x, we get: \\ 2 x + 2 (y - b) \cdot y^{'} = 0 \\ \Rightarrow (y - b) \cdot y^{'} = - x \\ \Rightarrow y - b = \frac{- x}{y^{'}} \\ Substituting the value of (y - b) in equation (i), we get: \end{array}$ $\begin{array}{l} x^{2} + {(\frac{- x}{y^{'}})}^{2} = 9 \\ \Rightarrow x^{2} [1 + \frac{1}{{(y^{'})}^{2}}] = 9 \\ \Rightarrow x^{2} ({(y^{'})}^{2} + 1) = 9 {(y^{'})}^{2} \\ \Rightarrow (x^{2} - 9) {(y^{'})}^{2} + x^{2} = 0 \\ This is the required differential equation. \end{array}$

Q11. $\begin{array}{l} Which of the following differential equations has \\ y = c_{1} e^{x} + c_{2} e^{- x} as the general solution? \end{array}$ $\begin{array}{l} (A) \frac{d^{2} y}{d x^{2}} + y = 0 \\ (B) \frac{d^{2} y}{d x^{2}} - y = 0 \end{array}$ $\begin{array}{l} (i i i) \frac{d^{2} y}{d x^{2}} + 1 = 0 \\ (i v) \frac{d^{2} y}{d x^{2}} - 1 = 0 \end{array}$

Answer. $\begin{array}{l} The given equation is: \\ y = c_{1} e^{x} + c_{2} e^{- x} . . . (i) \\ Differentiating with respect to x, we get: \\ \frac{d y}{d x} = c_{1} e^{x} - c_{2} e^{- x} \\ Again, differentiating with respect to x, we get: \end{array}$ $\begin{array}{l} \frac{d^{2} y}{d x^{2}} = c_{1} e^{x} + c_{2} e^{- x} \\ \Rightarrow \frac{d^{2} y}{d x^{2}} = y \\ \Rightarrow \frac{d^{2} y}{d x^{2}} - y = 0 \\ This is the required differential equation of the given equation of curve. \\ Hence, the correct answer is B. \end{array}$

Q12. $\begin{array}{l} Which of the following differential equation has y = x as one \\ of its particular solution? \end{array}$ $\begin{array}{l} (A) \frac{d^{2} y}{d x^{2}} - x^{2} \frac{d y}{d x} + x y = x \\ (B) \frac{d^{2} y}{d x^{2}} + x \frac{d y}{d x} + x y = x \\ (C) \frac{d^{2} y}{d x^{2}} - x^{2} \frac{d y}{d x} + x y = 0 \\ (D) \frac{d^{2} y}{d x^{2}} + x \frac{d y}{d x} + x y = 0 \end{array}$

Answer. The given equation of curve is y = x. Differentiating with respect to x, we get: $\frac{d y}{d x} = 1 (i)$ Again, differentiating with respect to x, we get: $\frac{d^{2} y}{d x^{2}} = 0 (i i)$ Now, on substituting the values of y, $\frac{d^{2} y}{d x^{2}}, and \frac{d y}{d x}$ from equation (i) and (ii) in each of the given alternatives, we find that only the differential equation given in alternative C is correct. $\begin{aligned} \frac{d^{2} y}{d x^{2}} - x^{2} \frac{d y}{d x} + x y & = 0 - x^{2} \cdot 1 + x \cdot x \\ = - x^{2} + x^{2} \\ = 0 \end{aligned}$ Hence, the correct answer is C.