NCERT Solutions Class 12 Maths Chapter-13 (Probability)Exercise 13.1

NCERT Solutions Class 12 Maths from class 12th Students will get the answers of Chapter-13 (Probability)Exercise 13.1 This chapter will help you to learn the basics and you should expect at least one question in your exam from this chapter.
We have given the answers of all the questions of NCERT Board Mathematics Textbook in very easy language, which will be very easy for the students to understand and remember so that you can pass with good marks in your examination.

NCERT Question-Answer

Class 12 Mathematics

Chapter-13 (Probability)

Questions and answers given in practice

Chapter-13 (Probability)

Exercise 13.1

Q1. Given that E and F are events such that P(E) = 0.6, P(F) = 0.3 and P(E ∩ F) = 0.2, find P(E|F) and P(F|E)

Answer. It is given that P(E) = 0.6, P(F) = 0.3, and P(E ∩ F) = 0.2 $\begin{array}{c}\Rightarrow P\left(E|F\right)=\frac{P(E\cap F)}{P\left(F\right)}=\frac{0.2}{0.3}=\frac{2}{3}\\ \Rightarrow P\left(F|E\right)=\frac{P(E\cap F)}{P\left(E\right)}=\frac{0.2}{0.6}=\frac{1}{3}\end{array}$

Q2. Compute P(A|B), if P(B) = 0.5 and P (A ∩ B) = 0.32

Answer. It is given that P(B) = 0.5 and P(A ∩ B) = 0.32 

$\Rightarrow P\left(\frac{A}{B}\right)=\frac{P(A\cap B)}{P\left(B\right)}=\frac{0.32}{0.5}=\frac{16}{25}$

Q3. If P(A) = 0.8, P (B) = 0.5 and P(B|A) = 0.4, find (i) P(A ∩ B) (ii) P(A|B) (iii) P(A ∪ B) 

Answer. It is given that P(A) = 0.8, P(B) = 0.5, and P(B|A) = 0.4 (i) P (B|A) = 0.4 $\begin{array}{cc}\therefore & \frac{P(A\cap B)}{P\left(A\right)}=0.4\\ \Rightarrow & \frac{P(A\cap B)}{0.8}=0.4\\ \Rightarrow P(A\cap B)& =0.32\\ \left(ii\right)P\left(A|B\right)& =\frac{P(A\cap B)}{P\left(B\right)}\\ & \Rightarrow P\left(A|B\right)=\frac{0.32}{0.5}=0.64\end{array}$ (iii) P(A∪B) = P(A) + P(B) – P(A∩B) ⇒ P(A∪B) = 0.8 + 0.5 – 0.32 = 0.98

Q4. Evaluate P(A ∪ B), if $2P\left(A\right)=P\left(B\right)=\frac{5}{13}\text{and}P\left(AB\right)=\frac{2}{5}$.

Answer. It is given that, $2P\left(A\right)=P\left(B\right)=\frac{5}{13}\text{and}P\left(AB\right)=\frac{2}{5}$ $\begin{array}{c}\Rightarrow P\left(A\right)=\frac{5}{26}\text{and}P\left(B\right)=\frac{5}{13}\\ P\left(A|B\right)=\frac{2}{5}\\ \Rightarrow \frac{P(A\cap B)}{P\left(B\right)}=\frac{2}{5}\\ \Rightarrow P(A\cap B)=\frac{2}{5}\times P\left(B\right)=\frac{2}{5}\times \frac{5}{13}=\frac{2}{13}\\ \text{It is known that,}P(A\cup B)=P\left(A\right)+P\left(B\right)-P(A\cap B)\end{array}$ $\begin{array}{c}\Rightarrow P(A\cup B)=\frac{5}{26}+\frac{5}{13}-\frac{2}{13}\\ \Rightarrow P(A\cup B)=\frac{5+10-4}{26}\\ \Rightarrow P(A\cup B)=\frac{11}{26}\end{array}$

Q5. If $P\left(A\right)=\frac{6}{11},P\left(B\right)=\frac{5}{11}\text{and}P(A\cup B)=\frac{7}{11}$ , find (i) P(A∩B) (ii) P(A|B) (iii) P(B|A) Determine P(E|F).

Answer. It is given that $P\left(A\right)=\frac{6}{11},P\left(B\right)=\frac{5}{11}\text{and}P(A\cup B)=\frac{7}{11}$ (i) $\begin{array}{c}P(A\cup B)=\frac{7}{11}\\ \therefore P\left(A\right)+P\left(B\right)-P(A\cap B)=\frac{7}{11}\\ \Rightarrow \frac{6}{11}+\frac{5}{11}-P(A\cap B)=\frac{7}{11}\\ \Rightarrow P(A\cap B)=\frac{11}{11}-\frac{7}{11}=\frac{4}{11}\end{array}$ (ii) It is known that, $P\left(A|B\right)=\frac{P(A\cap B)}{P\left(B\right)}$ $\Rightarrow P\left(A|B\right)=\frac{\frac{4}{11}}{\frac{5}{11}}=\frac{4}{5}$ (iii) It is known that , $P\left(B|A\right)=\frac{P(A\cap B)}{P\left(A\right)}$ $\Rightarrow P\left(B|A\right)=\frac{\frac{4}{11}}{\frac{6}{11}}=\frac{4}{6}=\frac{2}{3}$

Q6. A coin is tossed three times, where (i) E : head on third toss , F : heads on first two tosses (ii) E : at least two heads , F : at most two heads (iii) E : at most two tails , F : at least one tail

Answer. (i)$E=\{HHH,HTH,THH,TH\}F=\{HHH,HHT\}$$E\cap F=\left\{HHH\right\}$ $\begin{array}{c}P\left(F\right)=\frac{2}{8}=\frac{1}{4}\text{and}P(E\cap F)=\frac{1}{8}\\ P\left(E|F\right)=\frac{P(E\cap F)}{P\left(F\right)}=\frac{\frac{1}{8}}{\frac{1}{4}}=\frac{4}{8}=\frac{1}{2}\end{array}$ $E=\{HHH,HHT,HTH,THH\}$ (ii) $F=\{HHT,HTH,HTT,THH,THT,TH,TTT\}$ $E\cap F=\{HHT,HTH,THH\}$ $P(E\cap F)=\frac{3}{8}\text{and}P\left(F\right)=\frac{7}{8}$ $P\left(E|F\right)=\frac{P(E\cap F)}{P\left(F\right)}=\frac{\frac{3}{8}}{\frac{7}{8}}=\frac{3}{7}$ (iii) $E=\{HHH,HHT,HT,HTH,THH,THT,TH\}$ $\{HHT,HTT,HTH,THH,THT,TH,TTT\}$ $\begin{array}{c}\therefore E\cap F=\left\{HHT\text{, HTT, HTH, THH, THT, TTH}\right\}\\ P\left(F\right)=\frac{7}{8}\text{and}P(E\cap F)=\frac{6}{8}\\ \text{Therefore, P}\left(E|F\right)=\frac{P(E\cap F)}{P\left(F\right)}=\frac{\frac{6}{8}}{\frac{7}{8}}=\frac{6}{7}\end{array}$ $\begin{array}{c}E=\left\{HH\right\}F=\left\{TT\right\}\\ \therefore E\cap F=\Phi \end{array}$ $P\left(F\right)=1\text{and}P(E\cap F)$ $\begin{array}{c}\therefore P(E\cap F)=\\ \frac{P(E\cap F)}{P\left(F\right)}=\frac{0}{1}=0\end{array}$

Q7. Two coins are tossed once, where (i) E : tail appears on one coin, F : one coin shows head (ii) E : no tail appears, F : no head appears

Answer. If two coins are tossed once, then the sample space S is S = {HH, HT, TH, TT} (i) E = {HT, TH} F = {HT, TH} $\begin{array}{c}\therefore E\cap F=\{HT,TH\}\\ P\left(F\right)=\frac{2}{8}=\frac{1}{4}\\ P(E\cap F)=\frac{2}{8}=\frac{1}{4}\\ \therefore P\left(E|F\right)=\frac{P(E\cap F)}{P\left(F\right)}=\frac{2}{2}=1\end{array}$ (ii) E = {HH} F = {TT} ∴ E ∩ F = Φ P (F) = 1 and P (E ∩ F) = 0 $\therefore P\left(E|F\right)=\frac{P(E\cap F)}{P\left(F\right)}=\frac{0}{1}=0$

Q8. A die is thrown three times, E : 4 appears on the third toss, F : 6 and 5 appears respectively on first two tosses

Answer. If a die is thrown three times, then the number of elements in the sample space will be 6 × 6 × 6 = 216  $F=\left\{\right(6,5,1),(6,5,2),(6,5,3),(6,5,4),(6,5,5),(6,5,6\left)\right\}$ $\therefore E\cap F=\left\{\right(6,5,4\left)\right\}$ $\begin{array}{c}P\left(F\right)=\frac{6}{216}\text{and}P(E\cap F)=\frac{1}{216}\\ \therefore P\left(E|F\right)=\frac{P(E\cap F)}{P\left(F\right)}=\frac{\frac{1}{6}}{\frac{6}{216}}=\frac{1}{6}\end{array}$

Q9. Mother, father and son line up at random for a family picture E : son on one end, F : father in middle .

Answer. If mother (M), father (F), and son (S) line up for the family picture, then the sample space will be S = {MFS, MSF, FMS, FSM, SMF, SFM} E = {MFS, FMS, SMF, SFM} F = {MFS, SFM} $E\cap F=\{MFS,SFM\}$ $\therefore P\left(E|F\right)=\frac{P(E\cap F)}{P\left(F\right)}=\frac{\frac{1}{3}}{\frac{1}{3}}=1$

Q10. A black and a red dice are rolled. (a) Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5. (b) Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.

Answer. Let the first observation be from the black die and second from the red die. When two dice (one black and another red) are rolled, the sample space S has 6 × 6 = 36 number of elements. 1. Let A: Obtaining a sum greater than 9 $\begin{array}{c}=\left\{\right(4,6),(5,5),(5,6),(6,4),(6,5),(6,5\left)\right\}\text{B: Black die results in a}5.\\ =\left\{\right(5,1),(5,2),(5,3),(5,4),(5,5),(5,6\left)\right\}\\ \therefore A\cap B=\left\{\right(5,5),(5,6\left)\right\}\end{array}$ (a) The conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5, is given by P (A|B). $\therefore P\left(A|B\right)=\frac{P(A\cap B)}{P\left(B\right)}=\frac{\frac{2}{36}}{\frac{6}{35}}=\frac{2}{6}=\frac{1}{3}$ (b) E: Sum of the observations is 8. = {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)} F: Red die resulted in a number less than 4.$=\left\{\begin{array}{c}(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),\\ (3,1),(3,2),(3,3),(4,1),(4,2),(4,3),\\ (5,1),(5,2),(5,3),(6,1),(6,2),(6,3)\end{array}\right\}$ $\begin{array}{c}\therefore E\cap F=\left\{\right(5,3),(6,2\left)\right\}\\ P\left(F\right)=\frac{18}{36}\text{and}P(E\cap F)=\frac{2}{36}\end{array}$ The conditional probability of obtaining the sum equal to 8, given that the red die resulted in a number less than 4, is given by P (E|F). Therefore, $P\left(E|F\right)=\frac{P(E\cap F)}{P\left(F\right)}=\frac{\frac{2}{36}}{\frac{18}{36}}=\frac{2}{18}=\frac{1}{9}$

Q11. A fair die is rolled. Consider events E = {1,3,5}, F = {2,3} and G = {2,3,4,5} Find (i) P(E|F) and P(F|E) (ii) P(E|G) and P(G|E) (iii) P((E ∪ F)|G) and P((E ∩ F)|G)

Answer. When a fair die is rolled, the sample space S will be S = {1, 2, 3, 4, 5, 6} It is given that E = {1, 3, 5}, F = {2, 3}, and G = {2, 3, 4, 5} $\begin{array}{c}\therefore P\left(E\right)=\frac{3}{6}=\frac{1}{2}\\ P\left(F\right)=\frac{2}{6}=\frac{1}{3}\\ P\left(G\right)=\frac{4}{6}=\frac{2}{3}\\ \text{(i)}E\cap F=\left\{3\right\}\\ \therefore P(E\cap F)=\frac{1}{6}\end{array}$ $\begin{array}{c}\therefore P\left(E|F\right)=\frac{P(E\cap F)}{P\left(F\right)}=\frac{\frac{1}{6}}{\frac{1}{3}}=\frac{1}{2}\\ P\left(F|E\right)=\frac{P(E\cap F)}{P\left(E\right)}=\frac{\frac{1}{6}}{\frac{1}{2}}=\frac{1}{3}\end{array}$ (ii) $E\cap G=\{3,5\}$ $\begin{array}{c}\therefore P(E\cap G)=\frac{2}{6}=\frac{1}{3}\\ \therefore P\left(E|G\right)=\frac{P(E\cap G)}{P(E\cap G)}=\frac{\frac{1}{3}}{\frac{1}{3}}=\frac{1}{2}\\ P\left(G|E\right)=\frac{P(E\cap G)}{P\left(E\right)}=\frac{\frac{1}{3}}{\frac{1}{2}}=\frac{2}{3}\end{array}$ (iii) $E\cup F=\{1,2,3,5\}$ $\begin{array}{c}(E\cup F)\cap G=\{1,2,3,5\}\cap \{2,3,4,5\}=\{2,3,5\}\\ E\cap F=\left\{3\right\}\\ (E\cap F)\cap G=\left\{3\right\}\cap \{2,3,4,5\}=\left\{3\right\}\end{array}$ $\begin{array}{c}\therefore P(E\cup G)=\frac{4}{6}=\frac{2}{3}\\ P\left(\right(E\cup F)\cap G)=\frac{3}{6}=\frac{1}{2}\\ P(E\cap F)=\frac{1}{6}\\ P\left(\right(E\cap F)\cap G)=\frac{1}{6}\end{array}$ $\begin{array}{cc}\therefore P\left(\right(E\cup F\left)|G\right)& =\frac{P\left(\right(E\cup F)\cap G)}{P\left(G\right)}\\ & =\frac{\frac{1}{2}}{\frac{2}{3}}=\frac{1}{2}\times \frac{3}{2}=\frac{3}{4}\end{array}$ $\begin{array}{c}P\left(\right(E\cap F\left)|G\right)=\frac{P\left(\right(E\cap G)\cap G)}{P\left(G\right)}\\ =\frac{\frac{1}{6}}{\frac{6}{3}}=\frac{1}{6}\times \frac{3}{2}=\frac{1}{4}\end{array}$

Q12. Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls given that (i) the youngest is a girl, (ii) at least one is a girl?

Answer. Let b and g represent the boy and the girl child respectively. If a family has two children, the sample space will be S = {(b, b), (b, g), (g, b), (g, g)} Let A be the event that both children are girls. S = {(b, b), (b, g), (g, b), (g, g)} Let A be the event that both children are girls. $\therefore A=\left\{\right(g,g\left)\right\}$ (i) Let B be the event that the youngest child is a girl. $\begin{array}{c}\therefore B=\left[\right(b,g),(g,g\left)\right]\\ \Rightarrow A\cap B=\left\{\right(g,g\left)\right\}\\ \therefore P\left(B\right)=\frac{2}{4}=\frac{1}{2}\\ P(A\cap B)=\frac{1}{4}\end{array}$ The conditional probability that both are girls, given that the youngest child is a girl, is given by P (A|B). $P\left(A|B\right)=\frac{P(A\cap B)}{P\left(B\right)}=\frac{\frac{1}{4}}{\frac{1}{2}}=\frac{1}{2}$ Therefore, the required probability is $\frac{1}{2}$ (ii) Let C be the event that at least one child is a girl. $\begin{array}{c}\therefore C=\left\{\right(b,g),(g,b),(g,g\left)\right\}\\ \Rightarrow A\cap C=\{g,g\}\\ \Rightarrow P\left(C\right)=\frac{3}{4}\\ P(A\cap C)=\frac{1}{4}\end{array}$ The conditional probability that both are girls, given that at least one child is a girl, is given by P(A|C). Therefore, $P\left(A|C\right)=\frac{P(A\cap C)}{P\left(C\right)}=\frac{\frac{1}{4}}{\frac{3}{4}}=\frac{1}{3}$

Q13. An instructor has a question bank consisting of 300 easy True / False questions, 200 difficult True / False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions. If a question is selected at random from the question bank, what is the probability that it will be an easy question given that it is a multiple choice question?

Answer. The given data can be tabulated as 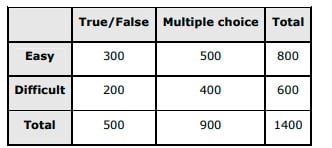 Let us denote E = easy questions, M = multiple choice questions, D = difficult questions, and T = True/False questions Total number of questions = 1400 Total number of multiple choice questions = 900 Therefore, probability of selecting an easy multiple choice question is $P(E\cap M)=\frac{500}{1400}=\frac{5}{14}$ Probability of selecting a multiple choice question, P (M), is $\frac{900}{1400}=\frac{9}{14}$ P (E|M) represents the probability that a randomly selected question will be an easy question, given that it is a multiple choice question. $P\left(E|M\right)=\frac{P(E\cap M)}{P\left(M\right)}=\frac{\frac{5}{14}}{\frac{9}{14}}=\frac{5}{9}$ Therefore, the required probability is $\frac{5}{9}$

Q14. Given that the two numbers appearing on throwing two dice are different. Find the probability of the event ‘the sum of numbers on the dice is 4’.

Answer. When dice is thrown, number of observations in the sample space = 6 × 6 = 36 Let A be the event that the sum of the numbers on the dice is 4 and B be the event that the two numbers appearing on throwing the two dice are different. $\therefore A=\left\{\right(1,3),(2,2),(3,1\left)\right\}$  $\begin{array}{c}A\cap B=\left\{\right(1,3),(3,1\left)\right\}\\ \therefore P\left(B\right)=\frac{30}{36}=\frac{5}{6}\text{and}P(A\cap B)=\frac{2}{36}=\frac{1}{18}\end{array}$ Let P (A|B) represent the probability that the sum of the numbers on the dice is 4, given that the two numbers appearing on throwing the two dice are different. $\therefore P\left(A|B\right)=\frac{P(A\cap B)}{P\left(B\right)}=\frac{\frac{1}{18}}{\frac{5}{6}}=\frac{1}{15}$ Therefore, the required probability is $\frac{1}{15}$.

Q15. Consider the experiment of throwing a die, if a multiple of 3 comes up, throw the die again and if any other number comes, toss a coin. Find the conditional probability of the event ‘the coin shows a tail’, given that ‘at least one die shows a 3’. In each of the Exercises 16 and 17 choose the correct answer:

Answer. The outcomes of the given experiment can be represented by the following tree diagram.The sample space of the experiment is, $S=\left\{\begin{array}{c}(1,H),(1,T),(2,H),(2,T),(3,1)(3,2),(3,3),(3,4),(3,5),(3,6),\\ (4,H),(4,T),(5,H),(5,T),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)\end{array}\right\}$ Let A be the event that the coin shows a tail and B be the event that at least one die shows 3. $\begin{array}{c}\therefore A=\left\{\right(1,T),(2,T),(4,T),(5,T\left)\right\}\\ B=\left\{\right(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(6,3\left)\right\}\\ \Rightarrow A\cap B=\varphi \\ \therefore P(A\cap B)=0\end{array}$ $\begin{array}{cc}\text{Then,}P\left(B\right)& =P\left(\right\{3,1\left\}\right)+P\left(\right\{3,2\left\}\right)+P\left(\right\{3,3\left\}\right)+P\left(\right\{3,4\left\}\right)+P\left(\right\{3,5\left\}\right)+P\left(\right\{3,6\left\}\right)+P\left(\right\{6,3\left\}\right)\\ & =\frac{1}{36}+\frac{1}{36}+\frac{1}{36}+\frac{1}{36}+\frac{1}{36}+\frac{1}{36}+\frac{1}{36}\\ & =\frac{7}{36}\end{array}$ Probability of the event that the coin shows a tail, given that at least one die shows 3, is given by P(A|B). Therefore, $P\left(A|B\right)=\frac{P(A\cap B)}{P\left(B\right)}=\frac{0}{\frac{7}{36}}=0$

Q16. If P(A) = 1 2 , P(B) = 0, then P(A|B) is (A) 0 (B) 1 2 (C) not defined (D) 1

Answer. It is given that , $P\left(A\right)=\frac{1}{2}\text{and}P\left(B\right)=0$ $P\left(A|B\right)=\frac{P(A\cap B)}{P\left(B\right)}=\frac{P(A\cap B)}{0}$ Therefore, P (A|B) is not defined. Thus, the correct answer is C.

Q17. If A and B are events such that P(A|B) = P(B|A), then (A) A ⊂ B but A ≠ B (B) A = B (C) A ∩ B = φ (D) P(A) = P(B).

Answer. It is given that, P(A|B) = P(B|A) $\Rightarrow \frac{P(A\cap B)}{P\left(B\right)}=\frac{P(A\cap B)}{P\left(A\right)}$ $\Rightarrow P\left(A\right)=P\left(B\right)$ Thus, the correct answer is D.

Chapter-13 (Probability)

• Exercise 13.2
• Exercise 13.3
• Exercise 13.4
• Exercise 13.5