NCERT Solutions Class 12 Maths Chapter-11 (Three Dimensional Geometry)Exercise 11.1
NCERT Solutions Class 12 Maths from class 12th Students will get the answers of Chapter-11 (Three Dimensional Geometry)Exercise 11.1 This chapter will help you to learn the basics and you should expect at least one question in your exam from this chapter.
We have given the answers of all the questions of NCERT Board Mathematics Textbook in very easy language, which will be very easy for the students to understand and remember so that you can pass with good marks in your examination.
We have given the answers of all the questions of NCERT Board Mathematics Textbook in very easy language, which will be very easy for the students to understand and remember so that you can pass with good marks in your examination.
NCERT Question-Answer
Class 12 Mathematics
Chapter-11 (Three Dimensional Geometry)
Questions and answers given in practice
Chapter-11 (Three Dimensional Geometry)
Exercise 11.1
Q1. If a line makes angles 90°, 135°, 45° with the x, y and z-axes respectively, find its direction cosines.
Answer. Therefore, the direction cosines of the line are .
Q2. Find the direction cosines of a line which makes equal angles with the coordinate axes.
Answer. Let the direction cosines of the line make an angle a with each of the coordinate axes. Thus, the direction cosines of the line, which is equally inclined to the coordinate axes, are .
Q3. If a line has the direction ratios –18, 12, – 4, then what are its direction cosines ?
Answer. If a line has the direction ratios of -18, 12, and -4 then its direction cosines are Thus, the direction cosines are .
Q4. Show that the points (2, 3, 4), (– 1, – 2, 1), (5, 8, 7) are collinear.
Answer.
Q5. Find the direction cosines of the sides of the triangle whose vertices are (3, 5, – 4), (– 1, 1, 2) and (– 5, – 5, – 2).
Answer. The vertices of . 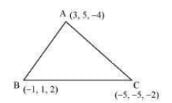 The direction ratios of sides AB are Therefore, the direction cosines of AB are The direction ratios of CA are Therefore, the direction cosines of AC are
The direction ratios of sides AB are Therefore, the direction cosines of AB are The direction ratios of CA are Therefore, the direction cosines of AC are
 The direction ratios of sides AB are Therefore, the direction cosines of AB are The direction ratios of CA are Therefore, the direction cosines of AC are
The direction ratios of sides AB are Therefore, the direction cosines of AB are The direction ratios of CA are Therefore, the direction cosines of AC are 



