NCERT Solutions Class 12 Maths Chapter-10 (Vector Algebra) Miscellaneous Exercise
NCERT Solutions Class 12 Maths from class
12th Students will get the answers of
Chapter-10 (Vector Algebra)Miscellaneous Exercise This chapter will help you to learn the basics and you should expect at least one question in your exam from this chapter.
We have given the answers of all the questions of
NCERT Board Mathematics Textbook in very easy language, which will be very easy for the students to understand and remember so that you can pass with good marks in your examination.
Q1. Write down a unit vector in KY-plane, making an angle of 30∘ with the positive direction of x-axis.
Answer. If →r is a unit vector in the XY-plane, then →r=cosθ^i+sinθ^j Here, θ is the angle made by the unit vector with the positive direction of the x -axis. Therefore, for θ=30∘: →r=cos30∘^i+sin30∘^j=√32^i+12^j Hence, the required unit vector is 2^i+12^j
Q2. Find the scalar components and magnitude of the vector joining the points P(x1,y1,z1) and Q(x2,y2,z2)
Answer. The vector joining the points (x1,y1,z1) and Q(x2,y2,z2) can be obtained by ¯¯¯¯¯¯¯¯PQ= Position vector of Q− Position vector of P =(x2−x1)^i+(y2−y1)^j+(z2−z1)^k|−−→PQ|=√(x2−x1)2+(y2−y1)2+(z2−z1)2 Hence, the scalar components and the magnitude of the vector joining the given points are respectively {(x2−x1),(y2−y1),(z2−z1)} and √(x2−x1)2+(y2−y1)2+(z2−z1)2
Q3. A girl walks 4 km towards west, then she walks 3 km in a direction 30∘east of north and stops. Determine the girl's displacement from her initial point of departure.
Answer. Let O and B be the initial and final positions of the girl respectively. Then, the girl's position can be shown as: 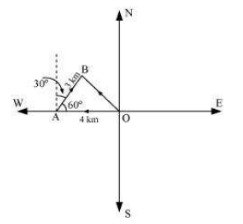 −−→OA=−4^i−−→AB=^i|−−→AB|cos60∘+^j|−−→AB|sin60∘ =^i3×12+^j3×√32=32^i+3√32^j −−→OB=−−→OA+−−→AB=(−4^i)+(32^i+3√32^j)=(−4+32)^i+3√32^j=(−8+32)^i+3√32^j=−52^i+3√32^3 Hence, the girl's displacement from her initial point of departure is −52^i+3√32^j
−−→OA=−4^i−−→AB=^i|−−→AB|cos60∘+^j|−−→AB|sin60∘ =^i3×12+^j3×√32=32^i+3√32^j −−→OB=−−→OA+−−→AB=(−4^i)+(32^i+3√32^j)=(−4+32)^i+3√32^j=(−8+32)^i+3√32^j=−52^i+3√32^3 Hence, the girl's displacement from her initial point of departure is −52^i+3√32^j
Q4. If →a=→b+→c, then is it true that =|→b|+|→c|? Justify your answer.
Answer. ΔABC, let −−→CB=→a,−−→CA=→b, and −−→AB=→c(as shown in the following figure) 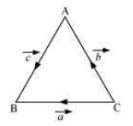 Now, by the triangle law of vector addition we have →a=→b+→c It is clearly known that|¯¯¯a|,|→b|, and |→c| Also, it is known that the sum of the lengths of any two sides of a triangle is greater than the third side. ∴|¯¯¯a|<|→b|+|¯¯c| Hence it is not true that |→a|=|→b|+|→c|
Now, by the triangle law of vector addition we have →a=→b+→c It is clearly known that|¯¯¯a|,|→b|, and |→c| Also, it is known that the sum of the lengths of any two sides of a triangle is greater than the third side. ∴|¯¯¯a|<|→b|+|¯¯c| Hence it is not true that |→a|=|→b|+|→c|
Q5. Find the value of x x for which x(^i+^j+^k) is a unit vector .
Answer. x(^i+^j+^k) is a unit vector if |x(^i+^j+^k)|=1 Now, |x(^i+^j+^k)|=1⇒√x2+x2+x2=1⇒√3x2=1⇒√3x=1⇒x=±1√3
Q6. Find a vector of magnitude 5 units, and parallel to the resultant of the vectors →a=2^i+3^j−^k and →b=^i−2^j+^k
Answer. →a=2^i+3^j−^k and →b=^i−2^j+^k Let →c be the resultant of →a and →b Then, →c=→a+→b=(2+1)^i+(3−2)^j+(−1+1)^k=3^i+^j →c=→a+→b=(2+1)^i+(3−2)^j+(−1+1)^k=3^i+^j∴|→c|=√32+12=√9+1=√10∴^c=→c|→c|=(3^i+^j)√10 Hence, the vector of magnitude 5 units and parallel to the resultant of vectors →a and →b is ±5⋅^c=±5⋅1√10(3^i+^j)=±3√10^i2±√102^j
Q7. If →a=^i+^j+^k,→b=2^i−^j+3^k and →c=^i−2^j+^k, find a unit vector parallel to the vector 2→a−→b+3→c
Answer. we have, →a=^i+^j+^k,→b=2^i+3^k and →c=^i−2^j+^k2→a−→b+3→c=2(^i+^j+^k)−(2^i−^j+3^k)+3(^i−2^j+^k) =2^i+2^j+2^k−2^i+^j−3^k+3^i−6^j+3^k=3^i−3^j+2^k|2→a−→b+3c|=√32+(−3)2+22=√9+9+4=√22 Hence, the unit vector along 2→a−→b+3→c is 2→a−→b+3→c|2→a−→b+3→c=3^i−3^j+2^k√22=3√22^i−3√22^j+2√22^k
Q8. Show that the points A (1, -2, -8), B (5, 0, -2) and C (11, 3, 7) are collinear, and find the ratio in which B divides AC.
Answer. The given points are A(1,−2,−8),B(5,0,−2), and C(11,3,7) . ∴−−→AB=(5−1)^i+(0+2)^j+(−2+8)^k=4^i+2^j+6^k −−→BC=(11−5)^i+(3−0)^j+(7+2)^k=6^i+3^j+9^k−−→AC=(11−1)^i+(3+2)^j+(7+8)^k=10^i+5^j+15^k|−−→AB|=√42+22+62=√16+4+36=√56=2√14|−−→BC|=√62+32+92=√36+9+81=√126=3√14|−−→AC|=√102+52+152=√100+25+225=√350=5√14 Thus, the given points A,B, and C are collinear. Now, let point B divide AC in the ratio λ:1 . Then, we have: −−→OB=λ−−→OC+−−→OA(λ+1) −−→OB=λ−−→OC+−−→OA(λ+1)⇒5^i−2^k=λ(11^i+3^j+7^k)+(^i−2^j−8^k)λ+1 ⇒(λ+1)(5^i−2^k)=11λ^i+3λ^j+7λ^k+^i−2^j−8^k⇒5(λ+1)^i−2(λ+1)^k=(11λ+1)^i+(3λ−2)^j+(7λ−8)^k On equating the corresponding components, we get: 5(λ+1)=11λ+1⇒5λ+5=11λ+1⇒6λ=4⇒λ=46=23 Hence, point B divides AC in the ratio 2:3 .
Q9. Find the position vector of a point R which divides the line joining two points P and Q Whose position vector are (2→a+→b) and (→a−3→b) externally in the ratio 1:2 Also, show that P is the mid point of the line segment RQ.
Answer. It is given that ¯¯¯¯¯¯¯¯OP=2→a+→b,−−→OQ=→a−3→b It is given that point R divides a line segment joining two points P and Q externally in the ratio 1:2. Then, on using the section formula, we get: −−→OR=2(2→a+→b)−(→a−3→b)2−1=4→a+2→b−→a+3→b1=3→a+5→b Therefore, the position vector of point R is 3→a+5→b Position vector of the mid-point of RQ=−−→OQ+−−→OR2=(→a−3→b)+(3→a+5→b)2=2→a+→bOP Hence, P is the mid-point of the line segment RQ.
Q10. The two adjacent sides of a parallelogram are 2^i−4^j+5^k and ^i−2^j−3^k . Find the unit vector parallel to its diagonal. Also, find its area.
Answer. Adjacent sides of a parallelogram are given as: →a=2^i−4^j+5^k and →b=^i−2^j−3^k Then, the diagonal of a parallelogram is given by →a+→b →a+→b=(2+1)^i+(−4−2)^j+(5−3)^k=3^i−6^j+2^k Thus, the unit vector parallel to the diagonal is →a+→b|→a+→b|=3^i−6^j+2^k√32+(−6)2+22=3^i−6^j+2^k√9+36+4=3^i−6^j+2^k7=37^i−67^j+27^k ∴ Area of parallelogram ABCD=|→a×→b| →a×→b=∣∣
∣
∣∣^i^j^k2−451−2−3∣∣
∣
∣∣=^i(12+10)−^j(−6−5)+^k(−4+4)=22^i+11^j=11(2^i+^j) ∴|→a×→b|=11√22+12=11√5 Hence, the area of the parallelogram is 11√5 square units.
Q11. Show that the direction cosines of a vector equally inclined to the axes OX, OY and OZ are 1√3,1√3,1√3
Answer. Let a vector be equally inclined to axes ox, oy, and oz at angle a . Then, the direction cosines of the vector are cos a,cosa,a and cos a . Now, cos2α+cos2α+cos2α=1⇒3cos2α=1⇒cosα=1√3 Hence, the direction cosines of the vector which are equally inclined to the axes 1√3,1√3,1√3
Q12. Let →a=^i+4^j+2^k,→b=3^i−2^j+7^k and →c=2^i−^j+4^k . Find a vector ¯¯¯d Perpendicular to both →a and →b, and →c→d=15
Answer. Let ¯¯¯d=d1^i+d2^j+d3^k since ¯¯¯d is perpendicular to both →a and →b , we have: →d⋅→a=0⇒d1+4d2+2d3=0 And →d⋅→b=0⇒3d1−2d2+7d3=0 Also, it is given that: →c⋅→d=15⇒2d1−d2+4d3=15 On solving (i),(ii), and (iii), we get: d1=1603,d2=−53 and d3=−703∴→d=1603^i−53^j−703˙k=13(160^i−5^j−70^k) Hence the required vector is 313(160^i−5^j−70^k)
Q13. The scalar product of the vector ^i+^j+^k with a unit vector along the sum of vectors 2^i+4^j−5^k and λ^i+2^j+3^k is equal to one. Find the value of λ
Answer. (2^i+4^j−5^k)+(λ^i+2^j+3^k)=(2+λ)^i+6^j−2^k Therefore, unit vector along (2+λ)^i+6^j−2^j√(2+λ)2+62+(−2)2=(2+λ)^i+6^j−2^k√4+4λ+λ2+36+4=(2+λ)^i+6^j−2^k√λ2+4λ+44 Scalar product of (t′+^j+^k) with this unit vector is 1 ⇒(^i+^j+^k)⋅(2+λ)^i+6^j−2^k√λ2+4λ+44=1⇒(2+λ)+6−2√λ2+4λ+44=1⇒√λ2+4λ+44=λ+6⇒λ2+4λ+44=λ+6⇒82+4λ+44=λ2+12λ+36⇒λ=1 Hence, the value of λ is 1 .
Q14. If →a,→b,→c are mutually perpendicular vectors of equal magnitudes, show that the vector →a+→b+→c is equally inclined to →a,→b and →c
Answer. since →a,→b, and →c are mutually perpendicular vectors, we have →a⋅→b=→b⋅→c=→c⋅→a=0 It is given that: |→a|=|→b|=|→c| Let vector →a+→b+→c be inclined to →a,→b, and →c at angles θ1,θ2, and θ3 respectively. Then, we have: cosθ1=(→a+→b+→c)⋅→a|→a+¯¯b+→c||→a|=→a⋅→a+→b⋅→a+→c⋅→a|→a+→b+→c|→a| =|→a|2|→a+→b+→c|→a=|→a|→a+b+→c| cosθ2=(→a+→b+→c)⋅→b|→u+→b+→c||→b|=→a⋅→b+→b⋅→b+→c⋅→b|→u+→b+→c|⋅|→b| =|→b|2|→a+→b+→c|⋅|→b|=|→b|→a+→b+→c| cosθ3=(→a+→b+→c)⋅→c|→a+→b+→c||→c|=→a⋅→c+→b⋅→c+→c⋅→c|→a+→b+→c|→c|=|¯¯c|2|→a+→b+→c|→c|=|→c|→a+→b+→c| Now, as |→a|=|→b|=|→c|,cosθ1=cosθ2=cosθ3∴θ1=θ2=θ3 Hence, the vector (→a+→b+→c) is equally inclined to →a,→b, and →c
Q15. Prove that (→a+→b)⋅(→a+¯¯b)=|→a|2+|→b|2, if and only if →a,→b are perpendicular, given →a≠→0,→b≠→0
Answer. (→a+→b)⋅(→a+→b)=|→a|2+|→b|2⇔→a⋅→a+→a⋅→b+→b⋅→a+→b⋅→b=|→a|2+|→b⇔2→a⋅→b=0⇔→a⋅→b=0∴→a and →b are perpendicular.
Q16. If θ is the angle between two vectors →a and →b, then →a→b≥0 (A)0<θ<π2(B)0≤θ≤π2(C)0<θ<π(D)0≤θ≤π
Answer. Let θ be the angle between two vectors →a and →b Then, without loss of generality, →a and →b are non-zero vectors so that |→a| and |→b| are positive It is known that ¯¯¯a⋅→b=|→a|→b|cosθ∴→a⋅→b≥0⇒cosθ|cosθ≥0⇒cosθ≥0⇒0≤θ≤π2 Hence, →a→b≥0 when The correct answer is B.
Q17. Let →a and →b be two unit vectors and θ is the angle between them. Then →a+→b is a unit vector if (A)θ=π4 (B)θ=π3 (C)θ=π2 (D)θ=2π3θ=2π3
Answer. Let →a and →b be two unit vectors and θ be the angle between them. Then, |→a|=|→b|=1 Now, →a+→b is a unit vector if |→a+→b|=1 |→a+→b|=1⇒(→a+→b)2=1⇒(→a+→b)⋅(→a+→b)=1⇒→a⋅→a+→a⋅→b+→b⋅→a+→b→b=1⇒|→a|2+2→a→b+|→b|2=1 ⇒|→a|2+2→a→b+|→b|2=1⇒12+2|→a||→b|cosθ+12=1⇒1+2.1.1cosθ+1=1⇒cosθ=−12⇒θ=2π3 Hence, →a+→b is a unit vector if θ=2π3 The correct answer is D .
Q18. The value of ^i⋅(^j×^k)+^j⋅(^i×^k)+^k.(^i×^j) is is (A) 0 (B)-1 (C) 1 (D) 3
Answer. ^i⋅(^j×^k)+^j⋅(^i×^k)+^k⋅(^i×^j)=^i⋅^i+^j⋅(−^j)+^k⋅^k=1−^j⋅^j+1=1−1+1=1
Q19. θ is the angle between any two vectors →a and →b, then |=|→a×→b∣∣ when (A)0(B)π4(C)π2(D)n(A)0(B)π4(C)π2(D)n
Answer. Let θ be the angle between two vectors →a and →b Then, without loss of generality, →a and →b are non-zero vectors, so that |→a| and |→b| are positive |→a⋅→b|=|→a×→b| ⇒cosθ=sinθ⇒tanθ=1⇒θ=π4 Hence, |→a¯¯b|=|→a×→b| The correct answer is B.

 Now, by the triangle law of vector addition we have It is clearly known that Also, it is known that the sum of the lengths of any two sides of a triangle is greater than the third side. Hence it is not true that
Now, by the triangle law of vector addition we have It is clearly known that Also, it is known that the sum of the lengths of any two sides of a triangle is greater than the third side. Hence it is not true that 



