NCERT Solutions Class 8 गणित Chapter-16 संभावना (प्रायिकता)

NCERT Solutions Class 8  गणित 8 वीं कक्षा से Chapter-16 संभावना (प्रायिकता) के उत्तर मिलेंगे। यह अध्याय आपको मूल बातें सीखने में मदद करेगा और आपको इस अध्याय से अपनी परीक्षा में कम से कम एक प्रश्न की उम्मीद करनी चाहिए। हमने NCERT बोर्ड की टेक्सटबुक्स हिंदी गणित के सभी Questions के जवाब बड़ी ही आसान भाषा में दिए हैं जिनको समझना और याद करना Students के लिए बहुत आसान रहेगा जिस से आप अपनी परीक्षा में अच्छे नंबर से पास हो सके।

एनसीईआरटी प्रश्न-उत्तर

Class 8 गणित

पाठ-16 संभावना (प्रायिकता)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

 अभ्यास 16 (a)

प्रश्न 1.

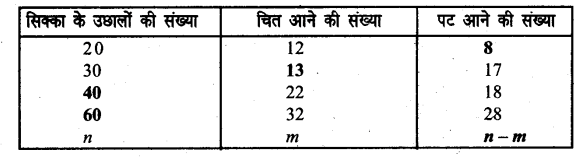
एक सिक्का कई बार उछालकर उसके शीर्ष (चित्र) तथा पूँछ (पट) आने की संख्या निम्नांकित सारणी में लिखी गई है। अपनी अभ्यास पुस्तिका में सारणी में रिक्त स्थानों की पूर्ति कीजिए।

हलः

प्रश्न 2.

एक पाँसे को कई बार फेंककर उसके ऊपर आने वाली संख्याएँ आगे अंकित सारणी में लिखी गई है। अपनी अभ्यास पुस्तिका में सारणी में रिक्त स्थान की पूर्ति कीजिए –

हलः

प्रश्न 3.

एक समांगी पाँसे के 48 बार फेंकने पर प्रत्येक फलक के ऊपर आने की संभावनाओं को समान मान लेने पर ज्ञात कीजिए कि अंक. 1, 2, 3, 4, 5, 6 में से प्रत्येक कितनी बार ऊपर आएगा?

हलः

अंकों की संख्या 6

पाँसा फेंका गया = 48 बार

∴ प्रत्येक अंक दिए पाँसों की संख्या = 48 ÷ 6 = 8 बार

प्रश्न 4.

एक समांगी पाँसे के 54 बार फेंकने पर यह पाया गया कि सम अंकों के ऊपर आने की संख्या 25 है, तो ज्ञात कीजिए कि विषम अंकों के ऊपर अपने की कुल संख्या कितनी होगी?

हलः

कुल फेंके गए पाँसे = 54 बार

सम अंकों के लिए फेंके गए पाँसे = 25 बार

∴ विषम अंकों के लिए फेंके गए पाँसों की संख्या = 54-25 = 29 बार।

अभ्यास – 16 (b)

प्रश्न 1.

दो सिक्के एक साथ 40 बार उछाले गए। यदि HH, HT, TH क्रमशः :9,8, 12 बार आए हों, । तो ज्ञात कीजिए कि TT कितनी बार आया होगा?

हलः

सिक्के उछाले गए = 40 बार

तीन परिणामों (HH, HT, TH) के लिए उछाले गए सिक्के (9+8+12) = 29 बार

∴ TT के लिए उछाले गए सिक्के = 40-29 = 11 बार

प्रश्न 2.

एक सिक्का 1000 बार उछाला गया और पाया गया कि चित 455 बार आया। ज्ञात कीजिए पट आने का प्रतिशत कितना है?

हलः

सिक्के उछाले गए = 1000 बार

सिक्के के चित आने की संख्या = 455

पट आने की संख्या = 1000 – 455 = 545

∴ 1000 बार उछालने पर पट आने की संख्या = 545

तो 100 बार उछालने पर पट आने का प्रतिशत =x100 = 54.5%

प्रश्न 3.

दो सिक्कों को एक साथ 400 बार उछालने पर देखा गया कि

दो चित                    90 बार

एक चित                  210 बार

कोई भी चितं नहीं   100 बार

इनसे प्रत्येक घटना के घटित होने का प्रतिशत ज्ञात कीजिए।

हलः

प्रश्न 4.

एक पाँसे को 1000 बार फेंकने पर प्राप्त परिणामों 1,2,3,4,5,6 बारम्बारताएँ निम्नांकित सारणी में दी हुई हैं। 1, 2, 3, 4, 5, 6 में प्रत्येक के आने का प्रतिशत ज्ञात कीजिए।

हलः

प्रश्न 5.

दो पाँसे एक साथ फेंके जाते हैं और पाँसों पर ऊपर आने वाले अंकों का योगफल लिया जाता है। निम्नांकित घटनाओं को समुच्चय के रूप में लिखिए –

(i) प्राप्त योग सम संख्या हो,

(ii) प्राप्त योग 3 का अपवर्त्य हो,

(iii) प्राप्त योग 4 से न्यून हो,

(iv) प्राप्त योग 10 से अधिक हो,

हलः

शिक्षक की सहायता से शिक्षार्थी स्वयं करें ।।

प्रश्न 6.

तीन सिक्के एक साथ उछाले जाते हैं तो निम्नांकित घटनाओं को समुच्चय के रूप में लिखिए।

(i) कोई चित प्रकट नहीं होता,

(ii) केवल एक चित होता है,

(iii) कम से कम दो चित प्रकट होते हैं,

(iv) तीनों चित आते हैं।

हलः

1. कोई चित प्रकट नहीं होता से आशय है कि तीनों पूँछ है = TTT
2. दो पूँछ और दर्शाए = HTT, THT, TTH
3. एक पूँछ और दर्शाए = HHT, HTH, HHT
4. तीनों सिर = HHH

प्रश्न 7.

दो पाँसों को एक साथ फेंकने पर दोनों पर सम अंकों के ऊपर आने की घटना का समुच्चय ज्ञात कीजिए।

हलः

दूसरे, चौथे व छठे बार फेंके जाने वाले पाँसों पर सम अंक 2, 4, 6= (2, 2), (2,4), (2,6), (4, 2), (4,4), (4, 6), (6, 2), (6, 4), (6, 6)

प्रश्न 8.

दो पाँसों को एक साथ फेंकने पर दोनों पर विषम अंकों के ऊपर आने की घटना का समुच्चय लिखिए।

हलः

प्रथम, तीसरी व पाँचवी बार फेंके जाने वाले पाँसों पर विषम अंक 1, 3, 5= (1,1), (1,3), (1,5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5)

प्रश्न 9.

दो पाँसों को एक साथ फेंकने पर दोनों पर अंकों का योग विषम संख्या आने का समुच्चय लिखिए।

हलः

पहले पाँसे पर सम अंक, दूसरे पर विषम अंक, तीसरे पर सम अंक, चौथे पर विषम अंक, पाँचवें पर सम और छठे पर विषम अंक रखने पर = (1,2), (1,4), (1,6), (2, 1), (2, 3), (2,5), (3, 2), (3,4), (3,6), (4,1), (4, 3), (4, 5), (5, 2), (5,4), (5, 6), (6, 1), (6, 3), (6, 5)

प्रश्न 10.

दो पाँसों को एक साथ फेंकने पर दोनों पर अंकों का योग अभाज्य संख्या होने का समुच्चय लिखिए।

हलः

शिक्षार्थी उपरोक्त प्रश्न की तरह हल करें।

प्रश्न 11.

एक लाटरी में 100 इनाम हैं जबकि उसके 100000 टिकट बिके हैं। इस लाटरी का एक टिकट खरीदने वाले व्यक्ति की इनाम जीतने की संभावना कितनी है?

हलः

इनाम प्राप्त करने की संभावना= 

एनसीईआरटी सोलूशन्स क्लास 8 गणित पीडीएफ

• 1 परिमेय संख्याओं पर संक्रियाएँ
• 2 वर्गमूल
• 3 घनमूल
• 4 सर्व समिकाएँ
• 5 बीजीय व्यंजकों का भाग एवं गुणनखंड
• 6 संख्याओं से खेल
• 7 युगपत समीकरण
• 8 वर्ग समीकरण 
• 9 समान्तर रेखाएँ 
• 10 चतुर्भुज की रचनाएँ
• 11 वाणिज्य गणित
• 12 बैंकिंग
• 13 वृत्त और चक्रीय चतुर्भज
• 14 वृत्त की स्पर्श रेखाएँ
• 15 सॉख्यिकी
• 17 कार्तीय तल
• 18 क्षेत्रमिति (मेंसुरेशन)