NCERT Solutions Class 8 गणित Chapter-14 (वृत्त की स्पर्श रेखाएँ)

NCERT Solutions Class 8 गणित 8 वीं कक्षा से Chapter-14 (वृत्त की स्पर्श रेखाएँ) के उत्तर मिलेंगे। यह अध्याय आपको मूल बातें सीखने में मदद करेगा और आपको इस अध्याय से अपनी परीक्षा में कम से कम एक प्रश्न की उम्मीद करनी चाहिए। हमने NCERT बोर्ड की टेक्सटबुक्स हिंदी गणित के सभी Questions के जवाब बड़ी ही आसान भाषा में दिए हैं जिनको समझना और याद करना Students के लिए बहुत आसान रहेगा जिस से आप अपनी परीक्षा में अच्छे नंबर से पास हो सके।

एनसीईआरटी प्रश्न-उत्तर

Class 8 गणित

पाठ-14 (वृत्त की स्पर्श रेखाएँ)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

अभ्यास 14 (a)

प्रश्न 1.

पार्श्व चित्र में O वृत्त का केंद्र है, और कुछ रेखाखंड खीचे गए हैं। ज्ञात कीजिए वृत्त की|

(i) दो छेदक रेखाएँ

(i) दो स्पर्श रेखाएँ

(iii) एक व्यास

(iv) एक स्पर्श बिन्दु और

(v) एक जीवा

हलः

AC तथा FC
GH JI FG
BOA
A या H
HE था DE

प्रश्न 2.

केंद्र O और त्रिज्या r वाले वृत्त की स्पर्श रेखा । है जो वृत्त को P पर स्पर्श करती है। यदि रेखा । पर स्थित कोई अन्य बिन्दु O है, तो निम्न कथनों में से सत्य अथवा असत्य कथन छाँटिएः

(i) OQ>r

(ii) OQ=r

(ii) OQ<r

(iv) OP>r

(v) OP = r

(vi) OP> r

हलः

सत्य
असत्य
असत्य
असत्य
सत्य
असत्य

प्रश्न 3.

जीवा और छेदक रेखा में क्या अंतर है? चित्र बनाकर स्पष्ट कीजिए।

हलः

जीवा – वृत्त पर स्थित किन्हीं दो बिन्दुओं को मिलाने वाले रेखाखंड को वृत्त की। जीवा कहते है। वृत्त पर स्थित बिन्दु A और B जीवाओं के अन्त्य बिन्दु हैं।

छेदक रेखा – उस रेखा को जो वृत्त को दो अलग-अलग बिन्दुओं पर प्रतिच्छेद करती है, वृत्त की छेदक रेखा कहते हैं। चित्र में PQ एक छेदक रेखा है।

प्रश्न 4.

2.0 सेमी त्रिज्या का एक वृत्त खींचिए। इस वृत्त के अभ्यन्तर , एक बिन्दु P लीजिए। ज्ञान कीजिए कि क्या P से होकर जाती हुई कोई ऐसी रेखा खींची जा सकती है जो वृत्त को स्पर्श करे?

हलः

नहीं, P से होकर स्पर्श रेखा नहीं खींची जा सकती है ।

प्रश्न 5.

किसी वृत्त की छेदक रेखा और स्पर्श रेखा में क्या भिन्नता होती है? चित्र खींचकर स्पष्ट कीजिए।

हलः

छेदक रेखा – किसी वृत्त की छेदक रेखा वह रेखा है। जो उस वृत्त को दो भिन्न बिन्दुओं पर प्रतिच्छेद करती है। चित्र में । छेदक रेखा है।

स्पर्श रेखा – किसी वृत्त की स्पर्श रेखा वह रेखा है जो उस वृत्त को केवल एक ही बिन्दु पर काटती है। चित्र में m स्पर्श रेखा है।

प्रश्न 6.

क्या व्यास वृत्त की छेदक रेखा है?

हलः

नहीं, स्पर्श रेखा है।

अभ्यास 14 (b)

प्रश्न 1.

पाश्र्व चित्र में O वृत्त का केंद्र है। PQ वृत्त की स्पर्श रेखा है और P स्पर्श बिन्दु है। ∠OPQ का मान कितना है?

हलः

∵ वृत्त की त्रिज्या स्पर्श रेखा के लम्बवत होती है।

∠OPQ = 90°

प्रश्न 2.

3.0 सेमी त्रिज्या का एक वृत्त खींचिए। वृत्त पर एक बिन्दु P लीजिए। बिन्दु P से वृत्त की स्पर्श रेखा खींचिए। रचना भी लिखिए।

हलः

रचना :

सर्वप्रथम 3 सेमी त्रिज्या का वृत्त खींचा।
इस वृत्त पर Pबिन्दु लेकर केन्द्र O से बिन्दु P को मिलाया।
OP के Pबिन्दु पर 90° का कोण बनाती हुई रेखा ABखींची।

अतः APB अभीष्ट स्पर्श रेखा है।

प्रश्न 3.

O केंद्र वाला एक वृत्त है। वृत्त पर एक बिन्दु P दिया है। बताइये कि बिन्दु P से वृत्त की कितनी स्पर्श रेखाएँ खींची जा सकती है। उत्तर का कारण चित्र खींचकर स्पष्ट कीजिए।

हलः

O केन्द्र वाला एक वृत्त है। वृत्त की परिधि पर बिन्दु P स्थित है। OP त्रिज्या के बिन्दु P से केवल एक ही लम्ब रेखा खींची जा सकती है, अतः बिन्दु P से वृत्त पर एक और केवल एक ही स्पर्श रेखा खींची जा सकती है।

प्रश्न 4.

किसी बिन्दु O को केंद्र मानकर 3.0 सेमी त्रिज्या का एक वृत्त खींचिए। चांदा और पटरी की सहायता से इस वृत्त की दो त्रिज्याएँ OA तथा OB इस प्रकारे खींचिए कि ∠AOB = 125°। बिन्दुओं A और B से वृत्त की स्पर्श रेखाएँ खींचिए। यदि दोनों रेखाएँ एक दूसरे को बिन्दु P पर। प्रतिच्छेद करें तो ∠ APB को नापकर लिखिए।

हलः

सर्वप्रथम O केन्द्र का एक वृत्त खींचा जिसकी त्रिज्या 3.0 सेमी है। त्रिज्या OA के बिन्दु 0 पर 125° का कोण बनाती हुई त्रिज्या OB खींची। अब बिन्दु A और B से त्रिज्याओं क्रमशः OA और OB पर लम्ब खींचे जो एक-दूसरे को P पर प्रतिच्छेद करती हैं। नापने पर,

∠APB = 55°

अभ्यास 14 (c)

प्रश्न 1.

निम्नलिखित कथनों में सत्य/असत्य कथन को अपनी अभ्यास पुस्तिका पर अलग-अलग करके लिखिए।

हलः

वृत्त की कोई स्पर्श रेखा तथा स्पर्श बिन्दु से खींची गयी त्रिज्या एक दूसरे पर लम्बे होते हैं। (सत्य)
किसी वृत्त की छेदिका, उस वृत्त को दो से अधिक बिन्दुओं पर प्रतिच्छेद करती है। (असत्य)
किसी वृत्त की स्पर्श रेखा, उस वृत्त को केवल दो बिन्दुओं पर प्रतिच्छेद करती है। (असत्य)
वृत्त के केन्द्र से उसकी किसी जीवा पर खींचा गया लम्ब, उस जीवा को समद्विभाजित करता है। (सत्य)

प्रश्न 2.

O केन्द्र लेकर 2.5 सेमी त्रिज्या का एक वृत्त खींचिए। इस वृत्त पर एक बिन्दु P लीजिए। त्रिज्या OP खींचिए । रेखाखण्ड OP के बिन्दु P पर लम्ब PT खींचिए। क्या PT वृत्त की स्पर्श रेखा है?

हलः

O वृत्त का केन्द्र तथा OP = 2.5 सेमी वृत्त की त्रिज्या है। रेखाखण्ड OP के बिन्दु P पर । लम्ब PT खींचा। ∠OPT = 90°

अतः PT वृत्त की स्पर्श रेखा है।

प्रश्न 3.

पार्श्व चित्र में O वृत्त का केन्द्र हैं। चित्र से निम्नांकित में रिक्त स्थानों की पूर्ति अपनी अभ्यास पुस्तिका पर कीजिए :

हलः

रेखाखण्ड AB वृत्त की जीवा है।
रेखाखण्ड OR वृत्त की त्रिज्या है।
रेखा CD वृत्त की छेदक रेखा है।
रेखा PQ वृत्त की स्पर्श रेखा है।

प्रश्न 4.

2.5 सेमी त्रिज्या तथा 0 केन्द्र वाला एक वृत्त खींचिए। इस वृत्त पर दो बिन्दु A और B इस प्रकार लीजिए कि ∠AOB = 60°। बिन्दुओं A और B से वृत्त की स्पर्श रेखाएँ क्रमशः AP तथा BP खींचिए। ∠APB नापकर लिखिए।

हलः

O वृत्ते को केन्द्र है केन्द्र O पर ∠AOB = 60° बिन्दु A और B से वृत्त की स्पर्श रेखाएँ AP तथा BP खींची जो कि एक दूसरे को बिन्दु P पर प्रतिच्छेद करती है।

∠OAP=∠OBP = 90°

∠APB = 180-60 = 120°

प्रश्न 5.

पार्श्व आकृति में PQ वृत्त का एक व्यास है तथा PR एवं QS उस वृत्त की क्रमशः P. एवं Q पर स्पर्श रेखाएँ हैं। क्या PR||Qs है? अपने उत्तर के लिए कारण भी दीजिए।

हलः

पार्श्व आकृति में PQ वृत्त का व्यास है तथा PR एवं Qs बिन्दु P तथा Q पर वृत्त की स्पर्श रेखाएँ हैं।

∠OPR = ∠OQS = 90°

OP⊥PR तथा OQ⊥QS

अतः PR||QS (क्योंकि वृत्त के केन्द्र से है तथा Q बराबर दूरी पर है। OP=OQ वृत्त की त्रिजाएँ)

प्रश्न 6.

पार्श्व आकृति में केन्द्र 9 वाले दो संकेन्द्रीय वृत्त (दोनों वृत्तों का एक ही केन्द्र O है) हैं। बड़े वृत्त की एक जीवा AB छोटे वृत्त की P पर स्पर्श रेखा है। क्या यह कहा सत्य होगा कि | AB बिन्दु P पर समद्विभाजित होती है? सकारणे उत्तर दीजिए।

हलः

पार्श्व आकृति में केन्द्र O (दोनों वृत्तों का केन्द्र है।) बड़े वृत्त की जीवा AB छोटे वृत्त की स्पर्श रेखा है।

∠OPA = ∠OPB = 90°

अतः वृत्त के केन्द्र से किसी जीवा पर डाला गया लम्ब जीवा को समद्विभाजित करता है। इसलिए बिन्दु P जीवा AB को समद्विभाजित करता है।

दक्षता अभ्यास-14

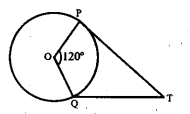
प्रश्न 1.

पार्श्व चित्र में O वृत्त का केंद्र है। इसकी दो त्रिज्याएँ OP : एवं OQ इस प्रकार हैं कि ∠POQ= 120°। बिन्दुओं P और Q से वृत्त की स्पर्श रेखाएँ खींची गई हैं जो एक दूसरे को T पर प्रतिच्छेद करती हैं। ∠PTQ का मान है: