NCERT Solutions Class 9 गणित Chapter-9 (समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल)
Class 9 गणित
पाठ-9 (समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल)
अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर
प्रश्नावली 9.1
प्रश्न 1.
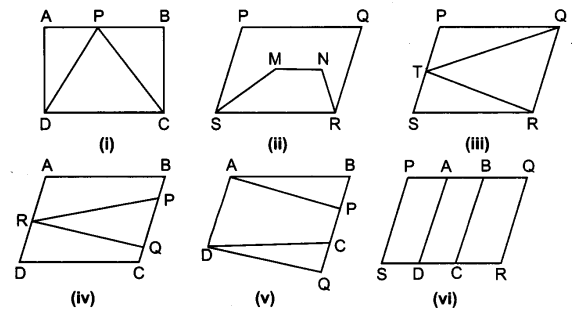
निम्नांकित आकृतियों में से कौन-सी आकृतियाँ एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित हैं? ऐसी स्थिति में, उभयनिष्ठ आधार और दोनों समान्तर रेखाएँ लिखिए।
हल :
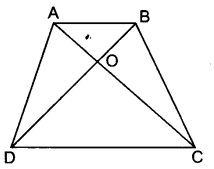
(i) इस आकृति में त्रिभुज PDC और चतुर्भुज ABCD का उभयनिष्ठ आधार DC है और DC की समान्तर रेखा पर त्रिभुज का शीर्ष P और चतुर्भुज के शीर्ष A व B स्थित हैं।
अत: ये आकृतियाँ (त्रिभुज और चतुर्भुज) एक ही आधार DC और एक ही समान्तर रेखाओं DC और AB के बीच स्थित हैं।
(ii) इस आकृति में दोनों चतुर्भुजों का आधार SR तो उभयनिष्ठ है परन्तु उनके शीर्ष P, Q व M, N आधार के समान्तर एक ही रेखा में नहीं हैं। अत: ये एक ही आधार और एक समान्तर रेखाओं के बीच स्थित नहीं हैं।
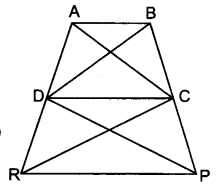
(iii) दी गई आकृति में ΔQRT और चतुर्भुज PQRS का आधार QR उभंयनिष्ठ है जबकि आधार QR के समान्तर एक ही रेखा पर ΔQRT का शीर्ष T और चतुर्भुज PQRS के शीर्ष P व S स्थित हैं। तब ΔQRT और चतुर्भुज PQRS एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित हैं। उभयनिष्ठ आधार QR तथा समान्तर रेखाएँ QR व PS हैं।
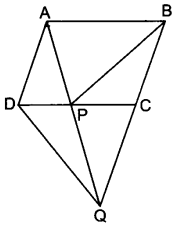
(iv) दी गई आकृति में एक समान्तर चतुर्भुज व एक त्रिभुज है जिनका कोई उभयनिष्ठ आधार नहीं है। अत: ये एक ही आधार व एक ही समान्तर रेखाओं के बीच स्थित नहीं हैं।
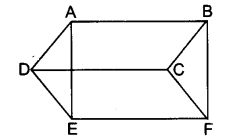
(v) इस आकृति में दो चतुर्भुज ABCD तथा APQD हैं जो एक ही आधार AD व एक ही समान्तर रेखाओं AD और PQ के बीच स्थित हैं।
(vi) दी गई आकृति में PQRS एक समान्तर चतुर्भुज है जिसके अन्तर्गत चतुर्भुज PADS, चतुर्भुज ABCD व चतुर्भुज BQRC तीन समान्तर चतुर्भुज समाहित हैं परन्तु इनका कोई उभयनिष्ठ आधार नहीं है।
अत: ये आकृतियाँ एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित नहीं हैं।
प्रश्नावली 9.2
प्रश्न 1.
दी गई आकृति में ABCD एक समान्तर चतुर्भुज है और AE ⊥ DC तथा CF ⊥ AD है। यदि AB = 16 सेमी, AE = 8 सेमी और CF = 10 सेमी है तो AD ज्ञात कीजिए।
हल :
ABCD एक समान्तर चतुर्भुज है जिसमें AB = CD और इन समान्तर भुजाओं के बीच की लाम्बिक दूरी = AE
समान्तर चतुर्भुज ABCD का क्षेत्रफल = CD x AE [CD = AB = 16 सेमी] = 16 x 8 = 128 वर्ग सेमी
पुनः समान्तर चतुर्भुज ABCD में, AD = BC और AD || BC के बीच की लाम्बिक दूरी = CF
समान्तर चतुर्भुज ABCD का क्षेत्रफल = AD x CF
AD x CF = 128 वर्ग सेमी
AD x 10 = 128
AD = 128 = 12.8 सेमी [CF = 10 सेमी]
अत: AD= 12.8 सेमी।
प्रश्न 2.
यदि E, F, G और H क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं के मध्य-बिन्दु हैं तो दर्शाइए कि ar (EFGH) = 
हल :
दिया है : ABCD एक समान्तर चतुर्भुज है जिसमें बिन्दु E, F, G और H क्रमशः समान्तर चतुर्भुज की भुजाओं AB, BC, CD व DA के मध्य-बिन्दु हैं।
सिद्ध करना है : ar (EFFG) =
रचना : EG को मिलाइए।
उपपत्ति : ABCD एक समान्तर चतुर्भुज है।
AB = CD और AB || CD
E, AB को मध्य-बिन्दु है और G, CD कां मध्य-बिन्दु है।
AE = EB =
DG = GC =
तब, AE = DG और AE || DG [AB = CD]
AEGD एक समान्तर चतुर्भुज है।
AEGD और ∆EGH उभयनिष्ठ आधार EG पर स्थित हैं। इनके शीर्ष A, D व में एक ही रेखा पर हैं जो EG के समान्तर है।
∆EGH का क्षेत्रफल =
इसी प्रकार,
∆EGF का क्षेत्रफल=
समीकरण (1) व (2) को जोड़ने पर,
∆EGH का क्षेत्रफल + ∆EGF का क्षेत्रफल =
EFGH का क्षेत्रफल =
=
अतः ar (EFGH =
Proved.
प्रश्न 3.
P और Q क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित बिन्दु हैं दर्शाइए कि ar (APB)= ar (BQC) है।
हल :
दिया है : ABCD एक समान्तर चतुर्भुज है, जिसमें भुजाओं DC और AD पर स्थित बिन्दु क्रमश: P और Q हैं।
रेखाखण्ड AP व BP और BQ व CQ खींचकर दो त्रिभुज APB और BQC प्राप्त किए गए हैं।
सिद्ध करना है : ar (∆APB) = ar (∆BQC)
अर्थात ∆APB का क्षेत्रफल = ∆BQC का क्षेत्रफल।
रचना : P से AB पर लम्ब PR और Q से BC पर लम्ब QS खींचे।
उपपत्ति : समान्तर चतुर्भुज ABCD में,
AB || DC और इनके बीच की लम्ब दूरी PR है।
समान्तर चतुर्भुज ABCD का क्षेत्रफल = एक भुजा x उस भुजा की सम्मुख भुजा से लम्ब दूरी
समान्तर चतुर्भुज ABCD का क्षेत्रफल = AB x PR …(1)
और ∆APB का क्षेत्रफल =
तब, समीकरण (1) व (2) से,
∆APB का क्षेत्रफल =
पुनः समान्तर चतुर्भुज ABCD में, BC || AD और इनके बीच की दूरी QS है।
समान्तर चतुर्भुज ABCD का क्षेत्रफल = एक भुजा x उस भुजा की सम्मुख भुजा से लम्ब दूरी = BC x QS
समान्तर चतुर्भुज ABCD का क्षेत्रफल = BC x QS
परन्तु ∆BQC का क्षेत्रफल =
तब, समीकरण (4) व (5) से,
∆BRC का क्षेत्रफल =
अब, समीकरण (3) व (6) से,
∆APB का क्षेत्रफल = ∆BQC का क्षेत्रफल
या ar(APB) = ar(BQC)
Proved.
प्रश्न 4.
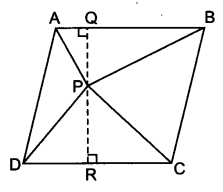
संलग्न आकृति में, P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिन्दु है। दर्शाइए कि
(i) ar (APB) + ar (PCD) =
(ii) ar (APD) + ar (PBC) = ar(APB) + ar(PCD)
हल :
दिया है : ABCD एक समान्तर चतुर्भुज है जिसके अभ्यन्तर में स्थित एक बिन्दु P है।
रेखाखण्ड PA, PB, PC और PD खींचे गए हैं।
जिससे चार त्रिभुज ∆APB, ∆PBC, ∆PCD और ∆APD प्राप्त होते हैं।
सिद्ध करना है :
(i) ar (APB) + ar (PCD) =
(ii) ar (APD) + ar (PBC) = ar (∆APB) + ar (∆PCD)
रचना : P से AB पर लम्ब PQ तथा CD पर लम्ब PR खींचिए।
उपपत्ति :
(i) समान्तर चतुर्भुज ABCD का क्षेत्रफल = भुजा x सम्मुख भुजा की लाम्बिक दूरी
समान्तर चतुर्भुज ABCD का क्षेत्रफल = AB x (PQ + PR) ……(1)
∆APB का क्षेत्रफल =
∆PCD का क्षेत्रफल =
जोड़ने पर,
∆APB का क्षेत्रफल + ∆PCD का क्षेत्रफल=
= (AB x PQ + AB x PR) (समान्तर चतुर्भुज ABCD में DC = AB)
=
समान्तर चतुर्भुज ABCD का क्षेत्रफले (समीकरण (1) से)
अत: ∆APB का क्षेत्रफल + ∆PCD का क्षेत्रफल =
ar (APB) + ar (PCD) =
Proved.
(ii) ar (APB) + ar (PCD)=
2 [ar(APB) + ar (PCD)] = ar (ABCD)
2 ar (APB) + 2 ar (PCD) = ar (APB) + ar (PBC)+ ar (PCD) + ar (APD)
2ar (APB) + 2 ar (PCD) – ar (APB) – ar (PCD) = ar (PBC) + ar (APD)
ar (APB) + ar (PCD) = ar (APD) + ar (PBC)
अत: ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
Proved.
प्रश्न 5.
दी गई आकृति में, PQRS और ABRS दो समान्तर चतुर्भुज हैं तथा X भुजा BR पर स्थित कोई बिन्दु है। दर्शाइए कि
(i) ar (PQRS) = ar(ABRS)
(ii) ar (AXS) =
हल :
दिया है : PQRS तथा ABRS दो समान्तर चतुर्भुज है जिनका PA उभयनिष्ठ आधार RS है।
भुजा BR पर कोई बिन्दु X है। रेखाखण्ड AX तथा SX खींचे गए हैं जिससे ∆AXS प्राप्त होता है।
सिद्ध करना है :
(i) ar(PQRS) = ar (ABRS)
(ii) ar (AXS) =
रचना : बिन्दु A से आधार SR पर लम्ब AE खींचिए और बिन्दु X से AS पर लम्ब XF खींचिए।
उपपत्ति :
(i) समान्तर चतुर्भुज PQRS में, PQ || RS और इनके बीच की लम्ब दूरी = AE है।
समान्तर चतुर्भुज PQRS का क्षेत्रफल = एक भुजा x उस भुजा की सम्मुख भुजा से लम्ब दूरी = SR x AE …..(1)
ar (PQRS) = SR x AE
समान्तर चतुर्भुज ABRS में,
AB || RS और इसके बीच की दूरी = AE है।
समान्तर चतुर्भुज ABRS का क्षेत्रफल = एक भुजा x उस भुजा की सम्मुख भुजा से लम्ब-दूरी = SR x AE ……(2)
ar (ABRS) = SR x AE
तब समीकरण (1) व (2) से,
ar (PQRS) = ar (ABRS)
Proved.
(ii) ABRS एक समान्तर चतुर्भुज है।
BR || AS और इनके बीच की लम्ब दूरी = XF
समान्तर चतुर्भुज ABRS का क्षेत्रफल = एक भुजा x उस भुजा से सम्मुख भुजा की लम्ब-दूरी = AS x FX …..(3)
ar (ABRS) = AS x (FX)
∆ AXS का क्षेत्रफल =
तब, समीकरण (3) से,
∆AXS का क्षेत्रफल =
ar (AXS) =
परन्तु हम सिद्ध कर चुके हैं कि ar (ABRS) = ar (PQRS)
अत: ar (AXS) =
Proved.
प्रश्न 6.
एक किसान के पास समान्तर चतुर्भुज PQRS के रूप का एक खेत था। उसने RS पर स्थित कोई बिन्दु A लिया और उसे Pऔर से मिला दिया। खेत कितने भागों में विभाजित हो गया है? इन भागों के आकार क्या हैं? वह किसान खेत में गेहूँ। और दालें बराबर-बराबर भागों में अलग-अलग बोना चाहता है। वह ऐसा कैसे करे?
हल :
माना किसान के पास चित्रानुसार PQRS समान्तर चतुर्भुज के आकार का एक खेत है। किसान ने भुजा RS पर एक बिन्दु A चुनकर उसे P तथा Q से मिला दिया।
खेत तीन त्रिभुजाकार भागों में विभाजित हो गया है। ये भाग ∆PSA, ∆PAQ तथा ∆QAR हैं।
किसान को गेहूँ और दालें बराबर क्षेत्रफलों में बोनी हैं इसलिए P से सम्मुख भुजा SR पर PN लम्ब डाला गया है।
∆PAQ का क्षेत्रफल =
PQRS एक समान्तर चतुर्भुज है। PQ = RS
तब, ∆PAQ का क्षेत्रफल =
∆PAQ का क्षेत्रफल =
=
= ∆PSA का क्षेत्रफल + ∆QAR का क्षेत्रफल
अत: किसान को ∆PAQ क्षेत्रफल में गेहूँ और ∆PSA तथा ∆QAR के क्षेत्रफल में दालें बोना चाहिए।
प्रश्नावली 9.3
प्रश्न 1.
दी गई आकृति में, ∆ABC की एक माध्यिका AD पर स्थित E कोई बिन्दु है। दर्शाइए कि ar (ABE) = ar (ACE) है।
हल :
दिया है : ∆ABC में BC का मध्य-बिन्दु D है जिससे AD त्रिभुज की एक माध्यिका है। माध्यिका AD पर एक बिन्दु E है।
सिद्ध करना है : ∆ABE का क्षेत्रफल = ∆ACE का क्षेत्रफल
अथवा ar (ABE) = ar (ACE)
∆ABC में,
D, BC का मध्य-बिन्दु है अर्थात AD माध्यिका है।
हम जानते हैं कि त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफल के दो त्रिभुजों में विभाजित करती है।
∆ABD का क्षेत्रफल = ∆ACD का क्षेत्रफल …..(1)
पुनः ∆BEC की माध्यिका ED है।
∆BED का क्षेत्रफल = ∆CDE का क्षेत्रफल …(2)
समीकरण (1) से (2) को घटाने पर,
∆ABD का क्षेत्रफल – ∆BED का क्षेत्रफल = ∆ACD का क्षेत्रफल – ∆CDE का क्षेत्रफल
∆ABE का क्षेत्रफल = ∆ACE का क्षेत्रफल
ar (ABE) = ar (ACE)
Proved.
प्रश्न 2.
∆ABC में, E माध्यिका AD का मध्य-बिन्दु है। दर्शाइए कि ar (BED) = ar (ABC) है।
हल :
दिया है : ∆ABC में AD त्रिभुज की माध्यिका है और AD का मध्य-बिन्दु E है।
∆ABD में, AD माध्यिका है।
∆ABD का क्षेत्रफल = ∆ACD का क्षेत्रफल
∆ABD का क्षेत्रफल + ∆ABD का क्षेत्रफल = ∆ABD का क्षेत्रफल + ∆ACD का क्षेत्रफल
2 ∆ABD का क्षेत्रफल = ∆ABC का क्षेत्रफल
∆ABD का क्षेत्रफल =
पुनः ∆ABD में, E, AD का मध्य-बिन्दु है।
BE, ∆ABD की माध्यिका है।
∆BED का क्षेत्रफल =
=
= 
ar (BED) =
Proved.
प्रश्न 3.
दर्शाइए कि समान्तर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।
हल :
दिया है: ABCD एक समान्तर चतुर्भुज है। जिसके विकर्ण AC और BD एक-दूसरे को बिन्दु 0 पर काटते हैं।
सिद्ध करना है : ∆ADO का क्षेत्रफल = ∆ABO का क्षेत्रफल = ∆BCO का क्षेत्रफल = ∆CDO का क्षेत्रफल
रचना : शीर्ष A से BD पर लम्ब AN खींचा।
उपपत्ति : ABCD एक समान्तर चतुर्भुज है और इसके विकर्ण AC व BD परस्पर बिन्दु O पर काटते हैं।
AB = CD तथा BC = AD
AO = CO तथा BO = DO
अब ∆BCO तथा ∆DAO में,
BC = DA (ऊपर सिद्ध किया है)
CO = AO (ऊपर सिद्ध किया है)
BO = DO (ऊपर सिद्ध किया है)
∆BCO = ∆ADO (S.S.S. से)
∆BCO का क्षेत्रफल = ∆ADO का क्षेत्रफल …(1)
इसी प्रकार, ∆ABO तथा ∆CDO भी सर्वांगसम होंगे।
∆ABO का क्षेत्रफल = ∆CDO का क्षेत्रफल …(2)
AN, BD पर लम्ब है।
∆ADO का क्षेत्रफल =
=
=
और ∆ABO का क्षेत्रफल =
=
=
∆ABO का क्षेत्रफल = ∆ADO का क्षेत्रफल
तब समीकरण (1), (2) व (3) से,
∆ABO का क्षेत्रफल = ∆BCO का क्षेत्रफल = ∆CDO का क्षेत्रफल = ∆ADO का क्षेत्रफल
अतः स्पष्ट है कि समान्तर चतुर्भुज के विकर्ण उसे समान क्षेत्रफल वाले चार त्रिभुजों में बाँटते हैं।
Proved.
प्रश्न 4.
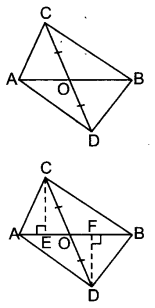
दी गई आकृति में, ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं। यदि रेखाखण्ड CD रेखाखण्ड AB से बिन्दु O पर समद्विभाजित होता है तो दर्शाइए कि ar (ABC) = ar (ABD) है।
हल :
दिया है। दो ∆ABC व ∆ABD एक ही आधार AB पर स्थित हैं।
AB रेखाखण्ड CD को O पर समद्विभाजित करता है।
सिद्ध करना है : त्रिभुज ABC का क्षेत्रफल = त्रिभुज ABD का क्षेत्रफल
अथवा
ar (ABC) = ar (ABD)
रचना : शीर्षों C तथा D से AB पर क्रमशः CE तथा DF लम्ब खींचे।
उपपत्ति : CE ⊥ AB और DF ⊥ AB (रचना से)
CE || DF; और CD एक तिर्यक रेखा है।
∠ECD = ∠FDC (एकान्तर कोण)
∠ECO = ∠FDO …(1)
अब ∆ECO और ∆FDO में,
∠ECO = ∠FDO [समीकरण (1) से]
CO = DO (O पर CD समद्विभाजित होता है)
∠COE = ∠DOF (शीर्षाभिमुख कोण हैं)
∆ECO = ∆FDO (A.S.A. से)
CE = DF (C.P.C.T.) …(2)
तब, ∆ABC का क्षेत्रफल =
=
=
= ∆ABD का क्षेत्रफल
अतः ∆ABC का क्षेत्रफल = ∆ABD का क्षेत्रफल
या
ar (ABC) = ar (ABC)
Proved.
प्रश्न 5.
D, E और F क्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिन्दु हैं। दर्शाइए कि
(i) BDEF एक समान्तर चतुर्भुज है।
(ii) ar (DEF) =
(iii) ar (BDEF) =
हल :
दिया है: ∆ABC में भुजाओं BC, CA और AB के मध्य-बिन्दु क्रमशः D, E और F हैं।
सिद्ध करना है:
(i) BDEF एक समान्तर चतुर्भुज है।
(ii) ar (DEF) =
(iii) ar (BDEF) =
उपपत्ति :
(i) ∆ABC में E, AC का मध्य-बिन्दु है और F, AB का मध्य-बिन्दु है।
EF =
D, BC का मध्य-बिन्दु है।
BD=
EF = BD और EF || BD
अत: BDEF एक समान्तर चतुर्भुज है।
Proved.
(ii) E और F क्रमश: AC और AB के मध्य-बिन्दु हैं।
EF = BC और EF || BC (मध्य-बिन्दु प्रमेय से)
परन्तु D, BC को मध्य-बिन्दु है।
CD =
EF = CD और EF || DC
DCEF एक समान्तर चतुर्भुज है।
FD = CE और FD || EC या FD || AC या FD || AE
BDEF एक समान्तर चतुर्भुज है।
DE = BF और DE || BF और DE || AB DE || AF
DE || AF और FD || AE
AEDF एक समान्तर चतुर्भुज है।
BDEF समान्तर चतुर्भुज है और FD उसका एक विकर्ण है।
∆DEF का क्षेत्रफल = ∆BDF का क्षेत्रफल ……(1)
DCEF समान्तर चतुर्भुज है और DE उसका एक विकर्ण है।
∆DEF का क्षेत्रफल = ∆DCE का क्षेत्रफल ……(2)
AEDF समान्तर चतुर्भुज है और EF उसका एक विकर्ण है।
∆DEF का क्षेत्रफल = ∆AEF का क्षेत्रफल ………(3)
समीकरण (1), (2) व (3) को जोड़ने पर,
3 ∆DEF’ का क्षेत्रफल = ∆BDF का क्षेत्रफल + ∆DCE का क्षेत्रफल + ∆AEF का क्षेत्रफल दोनों पक्षों में ∆DEF जोड़ने पर,
4 ∆DEF का क्षेत्रफल = (∆BDF + ∆DEC + ∆AEF + ∆DEF) का क्षेत्रफल
4 ∆DEF का क्षेत्रफल = ∆ABC का क्षेत्रफल
अतः ∆DEF का क्षेत्रफल = ∆ABC का क्षेत्रफल
अथवा ar (DEF) = ar (ABC)
Proved.
(iii) चतुर्भुज BDEF का क्षेत्रफल = ∆BDF का क्षेत्रफल + ∆DEF का क्षेत्रफल = ∆DEF का क्षेत्रफल + ∆DEF का क्षेत्रफल [समीकरण (1) से
= 2 ∆DEF का क्षेत्रफल = 2 x
=
अत: चतुर्भुज BDEF’ का क्षेत्रफल =
अथवा
ar (BDEF) = ar (ABC)
Proved.
प्रश्न 6.
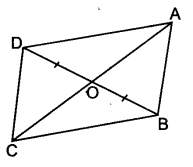
दी गई आकृति में, चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है। यदि AB = CD है तो दर्शाइए कि
(i) ar(DOC) = ar (AOB)
(ii) ar(DCB) = ar(ACB)
(iii) DA || CB या ABCD एक समान्तर चतुर्भुज है।
हल :
दिया है : ABCD एक चतुर्भुज है जिसमें विकर्ण AC, दूसरे विकर्ण BD को बिन्दु O पर इस प्रकार काटता है कि OB = OD भुजा AB, भुजा CD के बराबर है। सिद्ध करना है :
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB या ABCD एक समान्तर चतुर्भुज है।
रचना : शीर्ष B से AC पर लम्ब BF तथा शीर्ष D से AC पर लम्ब DG खींचे।
उपपत्ति:
(i) BF ⊥ AC और DG ⊥ AC
∠DGF = ∠BFG = 90° ये एकान्तर कोण हैं।
BF || DG
BF || DG और BD तिर्यक रेखा है।
∠BDG = ∠DBF (एकान्तर कोण)
∠ODG = ∠OBF
अब ∆DOG और ∆BOF’ में,
∠ODG = ∠OBF (ऊपर सिद्ध किया है)
OD = OB (दिया है)
∠DOG = ∠ BOF (शीर्षाभिमुख कोण युग्म)
∆DOG = ∆BOF (A.S.A. से)
ar (DOG) = ar (BOF) …(1)
∆CDG और ∆ABF में,
∠G = ∠F (DG ⊥ AC, BF ⊥ AC)
CD = AB (दिया है)
DG = BF (∆DOG = ∆BOF)
∆CDG = ∆ABF (R.H.S. से)
ar (CDG) = ar (ABF) …(2)
समीकरण (1) व (2) को जोड़ने पर,
ar (DOG) + ar (CDG) = ar (BOF) + ar (ABF)
अतः ar (DOC) = ar (AOB)
Proved.
(ii) ar (DOC) = ar (AOB) दोनों ओर ar (BOC) जोड़ने पर,
ar (DOC) + ar (BOC) = ar (AOB) + ar (BOC)
अतः ar (DCB) = ar (ACB)
Proved.
(iii) ∆DCB और ∆ACB के क्षेत्रफल समान हैं जैसा कि अभी सिद्ध किया है और दोनों त्रिभुज उभयनिष्ठ आधार BC पर स्थित हैं।
दोनों त्रिभुज एक ही समान्तर रेखाओं के बीच स्थित हैं।
तब, DA || CB
समीकरण (2) से,
∆CDG = ∆ABF
CG = AF …(3)
और समीकरण (1) से,
∆DOG = ∆BOF
GO = OF ……(4)
समीकरण (3) व (4) को जोड़ने पर,
CG + GO = OF + AF
OC = OA
O, विकर्ण CA का भी मध्य-बिन्दु है अर्थात विकर्ण परस्पर समद्विभाजित करते हैं।
अत: ABCD एक समान्तर चतुर्भुज है।
Proved.
प्रश्न 7.
बिन्दु D और E क्रमशः AABC की भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar (DBC) = ar (EBC) है। दर्शाइए कि DE || BC है।
हल :
दिया है: ∆ABC की दो भुजाओं AB तथा AC पर दो बिन्दु D और E इस प्रकार हैं। कि
∆DBC का क्षेत्रफल = ∆EBC का क्षेत्रफल।
सिद्ध करना है।
DE || BC
उपपत्ति :
ar (DBC) = ar (EBC)
∆DBC का क्षेत्रफल = ∆EBC का क्षेत्रफल
और दोनों उभयनिष्ठ आधार BC पर एक ही ओर स्थित हैं।
दोनों त्रिभुजों के शीर्ष BC के समान्तर एक ही रेखा पर स्थित होंगे।
अतः DE || BC
Proved.
प्रश्न 8.
XY त्रिभुज ABC की भुजा BC के समान्तर एक रेखा है। यदि BE || AC और CF || AB रेखा XY से क्रमशः E और F पर मिलती हैं तो दर्शाइए कि ar (ABE) = ar (ACF)
हल:
दिया है: ∆ABC की भुजा BC के समान्तर एक रेखा XY खींची गई है। बिन्दु B से AC के समान्तर रेखा BE खींची गई है जो XY से E पर मिलती है और इसी प्रकार बिन्दु C से AB के समान्तर एक रेखा CF खींची गई है जो XY से बिन्दु F पर मिलती है।
सिद्ध करना है : ar (ABE) = ar (ACF)
उपपत्ति : XY || BC और BE || AC
यहाँ समान्तर रेखा युग्म (XY, BC)को अन्य समान्तर रेखा युग्म (EB, AC) द्वारा काटने पर समान्तर चतुर्भुज AEBC प्राप्त होता है।
AB, समान्तर चतुर्भुज AEBC का विकर्ण है।
∆ABE का क्षेत्रफल = ∆ABC का क्षेत्रफल …(1)
XY || BC और CF || AB
अर्थात एक समान्तर रेखा युग्म (XY, BC) को दूसरे समान्तर रेखा युग्म (CF, AB) द्वारा काटने पर समान्तर चतुर्भुज ABCF प्राप्त होता है।
AC, समान्तर चतुर्भुज ABCF’ का विकर्ण है।
∆ABC का क्षेत्रफल = ∆ACF का क्षेत्रफल …(2)
समीकरण (1) व (2) से,
∆ABE का क्षेत्रफल = ∆ACF का क्षेत्रफल
या ar (ABE) = ar (ACF)
Proved.
प्रश्न 9.
समान्तर चतुर्भुज ABCD की एक भुजा AB को एक बिन्दु P तक बढ़ाया गया है। A से होकर CP के समान्त
र खींची गई रेखा बढ़ाई गई CB को Qपर मिलती है और फिर समान्तर चतुर्भुज PBQR को पूरा किया गया है। दर्शाइए कि ar (ABCD) = ar (PBQR) है।
हल :
दिया है : समान्तर चतुर्भुज ABCD की भुजा AB को किसी बिन्दु P तक बढ़ाया गया है। बिन्दु A से CP के समान्तर रेखा AQ है जो बढ़ी हुई CB से Q पर मिलती है। समान्तर चतुर्भुज PBQR को पूरा किया गया है।
सिद्ध करना है :
क्षेत्रफल (समान्तर चतुर्भुज ABCD) = क्षेत्रफल (समान्तर चतुर्भुज PBQR)
ar (ABCD) = ar (PBQR)
रचना : चतुर्भुज ABCD का विकर्ण AC तथा चतुर्भुज PBQR का विकर्ण PR खींचिए।
उपपत्ति : AQ || CP और ∆ACQ तथा ∆APQ का आधार AQ है और ये इन्हीं समान्तर रेखाओं के बीच स्थित हैं।
क्षेत्रफल (∆ACQ) = क्षेत्रफल (∆APQ)
क्षेत्रफल (∆ACB) + क्षेत्रफल (∆ABQ) = क्षेत्रफल (∆ABQ) + क्षेत्रफल (∆BPQ)
क्षेत्रफल (∆ACB) = क्षेत्रफल(∆BPQ) …(1)
∆ACB की भुजा AC, समान्तर चतुर्भुज ABCD का विकर्ण है और ∆BPQ की भुजा PQ, समान्तर चतुर्भुज PBQR का विकर्ण है।
क्षेत्रफल (∆ACB) =
क्षेत्रफल (∆BPQ) =
समीकरण (1), (2) तथा (3) से,
क्षेत्रफल (समान्तर चतुर्भुज ABCD) = क्षेत्रफल ( समान्तर चतुर्भुज PBQR)
अथवा ar (ABCD) = ar (PBQR)
Proved.
प्रश्न 10.
एक समलम्ब ABCD, जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ar (AOD) = ar (BOC) है।
हल :
दिया है : ABCD एक समलम्ब है जिसमें AB || DC है और समलम्ब के विकर्ण : AC और BD परस्पर O पर प्रतिच्छेद करते हैं।
सिद्ध करना है : ∆AOD का क्षेत्रफल = ∆BOC का क्षेत्रफल
ar (∆AOD) = ar (A BOC)
उपपत्ति : समलम्ब ABCD में AB || DC है और ∆ADC तथा ∆BDC दोनों का उभयनिष्ठ आधार DC है।
और दोनों के शीर्ष A तथा B, DC के समान्तर भुजा AB पर स्थित हैं।
∆ADC और ∆BDC एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित हैं।
∆ADC का क्षेत्रफल = ∆BDC को क्षेत्रफल
दोनों पक्षों से ∆DOC का क्षेत्रफल घटाने पर,
∆ADC का क्षेत्रफल – ∆DOC का क्षेत्रफल = ∆BDC का क्षेत्रफल – ∆DOC का क्षेत्रफल
∆AOD का क्षेत्रफल = ∆BOC का क्षेत्रफल
अथवा ar (AOD) = ar (BOC)
Proved.
प्रश्न 11.
दी गई आकृति में, ABCDE एक पंचभुज है। B से होकर AC के A समान्तर खींची गई रेखा बढ़ाई गई DC को F पर मिलती है। दर्शाइए कि
(i) ar (ACB) = ar (ACF)
(ii) ar(AEDF) = ar (ABCDE)
हल :
दिया है : दी गई आकृति में ABCDE एक पंचभुज है। रेखाखण्ड AC खींचा गया है और बिन्दु B से इसके समान्तर एक रेखा खींची गई है जो DC को बढ़ाने पर उससे बिन्दु F पर मिलती है।
सिद्ध करना है :
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
उपपत्ति :
(i) दिया है BF || AC
∆ACB और ∆ACF समान्तर रेखाओं BF और AC के बीच स्थित हैं और दोनों त्रिभुजों का उभयनिष्ठ आधार AC है।
त्रिभुज ACB का क्षेत्रफल = त्रिभुज ACF का क्षेत्रफल
ar (ACB) = ar (ACF)
Proved.
(ii) ar (ACB) = ar (ACF)
दोनों पक्षों में ar (ACDE) जोड़ने पर,
ar (ACDE) + ar (ACB) = ar (ACDE) + ar (ACF)
ar (ABCDE) = ar (AEDF)
अतः ar (ABCDE) = ar (AEDF)
Proved.
प्रश्न 12.
गाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखण्ड था। उस गाँव की ग्राम पंचायत ने उसके भूखण्ड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केन्द्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबन्ध के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखण्ड के संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखण्ड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
हल :
माना ABCD एक चतुर्भुजाकार भूखण्ड है जिसके एक कोने से कुछ भाग लेकर समान क्षेत्रफल का दूसरा भाग देना है जो खेत से संलग्न भी हो और बचे खेत के साथ मिलकर पूर्ण भूखण्ड का अधिगृहीत भूखण्ड त्रिभुजाकार बना सके।
चतुर्भुजाकार खेत का विकर्ण AC खींचिए।
बिन्दु D से DE || AC खींचिए जो बढ़ी हुई BC को E पर काटे। रेखाखण्ड AE खींचिए जो CD रेखा O पर काटे।
देखिए ∆ACD और ∆ACE एक ही आधार AC पर एक ही समान्तर रेखाओं AC व DE के बीच स्थित हैं।
ar (ACD) = ar (ACE)
ar (∆AOD) + ar (∆AOC) = ar (∆AOC) + ar (∆COE)
ar (AOD) = ar (COE)
अत: ∆AOD क्षेत्र लेकर उसके बचे भूखण्ड के क्षेत्र में क्षेत्र (∆COE) जोड़कर दे देना चाहिए।
प्रश्न 13.
ABCD एक समलम्ब है, जिसमें AB || DC है। AC के समान्तर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है। सिद्ध कीजिए कि ar (ADX) = ar (ACY) है।
हल :
दिया है : ABCD एक समलम्ब है जिसमें AB || DC है। विकर्ण AC खींचा गया है। AC के समान्तर एक रेखा खींची गई जो AB को X पर और BC को Y पर प्रतिच्छेद करती है। रेखाखण्ड DX और AY खींचे गए हैं जिनसे ∆ADX और ∆ACY बने हैं।
सिद्ध करना है : ar (ADX) = ar (ACY)
रचना : रेखाखण्ड CX खींचा।
उपपत्ति : AB पर एक बिन्दु X है और AB || DC है।
AX || DC तब ∆ADX और ∆ACX एक ही आधार AX पर एक ही समान्तर रेखाओं AX व DC के मध्य स्थित हैं।
ar (ADX) = ar (ACX) …(1)
पुनः XY || AC
तब ∆ACX और ∆ACY समान (उभयनिष्ठ) आधार AC पर समान्तर रेखाओं XY और AC के बीच स्थित है।
ar (ACX) = ar (ACY) …(2)
तब, समीकरण (1) व (2) से,
ar (ADX) = ar (ACY)
Proved.
प्रश्न 14.
दी गई आकृति में AP || BQ || CR है। सिद्ध कीजिए कि ar (AQC) = ar (PBR) है।
हल :
दिया है : दी गई आकृति में AP || BQ है और BQ || CR है। रेखाखण्ड AQ, CQ, BP और BR खींचे गए हैं।
सिद्ध करना है : ar (AQC) = ar (PBR)
उपपत्ति : AP || BQ;
∆ABQ और ∆PBQ का आधार BQ उभयनिष्ठ है और ये दोनों समान्तर रेखाओं AP व B के बीच स्थित हैं।
ar (ABQ) = ar (PBQ) …(1)
इसी प्रकार,
∆BCQ और ∆BQR का उभयनिष्ठ आधार BQ है तथा ये दोनों समान्तर रेखाओं BQ व CR के बीच स्थित हैं।
ar (BCQ) = ar (BQR) …..(2)
समीकरण (1) व (2) को जोड़ने पर,
ar (ABQ) + ar (BCQ) = ar (PBQ) + ar (BQR)
या ar (AQC)= ar (PBR)
Proved.
प्रश्न 15.
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते हैं कि ar (AOD) = ar (BOC) है। सिद्ध कीजिए कि ABCD एक समलम्ब है।
हल :
दिया है : ABCD में विकर्ण AC और BD परस्पर बिन्दु 0 पर एक-दूसरे को प्रतिच्छेद करते हैं और ∆AOD का क्षेत्रफल = ∆BOC का क्षेत्रफल।
सिद्ध करना है : ABCD एक समलम्ब है।
उत्पत्ति: ∆AOD का क्षेत्रफल = ∆BOC का क्षेत्रफल (दिया है)
दोनों ओर समान क्षेत्रफल ∆DOC जोड़ने पर,
∆AOD का क्षेत्रफल + ∆DOC को क्षेत्रफल = ∆DOC का क्षेत्रफल + ∆BOC का क्षेत्रफल
(∆AOD + ∆DOC) का क्षेत्रफल = (∆DOC + ∆BOC) का क्षेत्रफल
∆ADC का क्षेत्रफल = ∆BDC का क्षेत्रफल
उक्त दोनों त्रिभुजों का उभयनिष्ठ आधार DC है और दोनों का क्षेत्रफल समान है।
तबे, दोनों एक ही समान्तर रेखाओं के बीच स्थित होंगे।
AB || DC
अतः ABCD एक समलम्ब है।
Proved.
प्रश्न 16.
दी गई आकृति में, ar (DRC) = ar (DPC) है और ar (BDP) = ar (ARC) है। दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलम्ब हैं।
हल :
दिया है : दी गई आकृति में ∆DRC, ∆DPC, ∆BPD और ∆ARC इस प्रकार हैं कि
ar (DRC) = ar (DPC) और ar (BDP) = ar (ARC)
सिद्ध करना है : चतुर्भुज ABCD और चतुर्भुज DCPR समलम्ब हैं।
उपपत्ति : ∆DRC और ∆DPC में ज्ञात है कि ar (DRC) = ar (DPC) और दोनों त्रिभुजों का उभयनिष्ठ आधार DC है।
∆DRC और ∆DPC एक ही समान्तर रेखाओं के बीच स्थित हैं।
DC || RP …(1)
अतः चतुर्भुज DCPR एक समलम्ब है।
ar (BDP) = ar (ARC)
ar (BDC) + ar (DPC) = ar (DRC) + ar (ADC)
परन्तु ar (DPC) = ar (DRC) (दिया है)
घटाने पर, ar (BDC) = ar (ADC)
∆BDC और ∆ADC के क्षेत्रफल बराबर हैं और उनका उभयनिष्ठ आधार DC है।
तब ∆BDC और ∆ADC एक ही समान्तर रेखाओं के बीच स्थित हैं।
AB || DC …(2)
अतः चतुर्भुज ABCD का एक समलम्ब है। तब चतुर्भुज ABCD और चतुर्भुज DCPR दोनों ही समलम्ब हैं।
Proved.
प्रश्नावली 9.4 (ऐच्दिक)
प्रश्न 1.
समान्तर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए कि समान्तर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।
हल :
दिया है : समान्तर चतुर्भुज ABCD का आधार AB तथा इसी आधार AB पर ही समान क्षेत्रफल का आयत ABEF स्थित है।
सिद्ध करना है : समान्तर चतुर्भुज ABCD का परिमाप > आयत ABEF’ का परिमाप
उपपत्ति: ∆ADF में,
∠F = 90° (आयत का अन्त:कोण)
AF ⊥ EF
AF < AD (AD कर्ण है) …(1)
इसी प्रकार A BCE में,
∠E = 90° (आयत का बहिष्कोण = 90°)
BE ⊥ CD
BE < BC ( BC कर्ण है) …(2)
(AF + BE) < (AD + BC).
समीकरण (1) व (2) से
AB = EF (ABEF आयत है।)
AB = DC (ABCD समान्तर चतुर्भुज है।)
AB = EF = DC
दोनों ओर क्रमश: (AB + EF) और (AB + CD) जोड़ने पर,
AB + BE + EF + AF < AB + BC + CD + DA अतः समान्तर चतुर्भुज का परिमाप > आयत का परिमाप
Proved.
प्रश्न 2.
दी गई आकृति में, भुजा BC पर दो बिन्दु D और E इस प्रकार स्थित हैं। कि BD = DE = EC है। दर्शाइए कि ar (ABD) = ar (ADE) = ar (AEC) है।
क्या आप अब उस प्रश्न का उत्तर दे सकते हैं, जो आपने इस अध्याय की ‘भूमिका’ में छोड़ दिया था कि क्या बुधिया का खेत वास्तव में बराबर क्षेत्रफलों वाले तीन भागों में विभाजित हो गया है?
हल :
दिया है : भुजा BC पर D और E दो बिन्दु इस प्रकार स्थित हैं कि BD = DE = EC है।
सिद्ध करना है : ar (ABD) = ar (ADE) = ar (AEC)
रचना : शीर्ष से BC पर शीर्षलम्ब AP खींचा।
उपपत्ति : BD = DE = EC
तीनों त्रिभुजों के आधार समान हैं। यह भी स्पष्ट है कि तीनों त्रिभुजों की एक ही ऊँचाई AP है। तब तीनों त्रिभुजों के क्षेत्रफल भी समान होंगे।
अतः ar (ABD) = ar (ADE) = ar (AEC)
किसी त्रिभुज के आधार को n समान भागों में विभक्त कर सम्मुख शीर्ष से मिलाने पर त्रिभुज समान n भागों में विभक्त हो जाता है।
अत: किसान बुधिया द्वारा विभाजित किया गया क्षेत्र (खेत) वास्तव में बराबर क्षेत्रफलों वाले तीन भागों में विभाजित हो गया था।
Proved.
प्रश्न 3.
दी गई आकृति में, ABCD, DCFE और ABFE समान्तर चतुर्भुज हैं। दर्शाइए कि ar (ADE) = ar (BCF) है।
हल :
दिया है : दी गई आकृति में चतुर्भुज ABCD, चतुर्भुज DCFE और चतुर्भुज ABFE समान्तर चतुर्भुज हैं।
सिद्ध करना है : ar (ADE) = ar (BCF)
उपपत्ति: ABCD एक समान्तर चतुर्भुज है।
AD = BC
DCFE एक समान्तर चतुर्भुज है। DE = CF
ABFE एक समान्तर चतुर्भुज है। AE = BF
अब ∆ADE तथा ∆BCF में,
AD = BC (ऊपर सिद्ध किया है)
DE = CF (ऊपर सिद्ध किया है)
AE = BF (ऊपर सिद्ध किया है)
तब त्रिभुजों की सर्वांगसमता के परीक्षण (S.S.S.) से,
∆ADE = ∆BCF
ar (∆ADE) = ar (∆BCF)
Proved.
प्रश्न 4.
दी गई आकृति में, ABCD, एक समान्तर चतुर्भुज है। BC को बिन्दु २ तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ भुजा DC को P पर प्रतिच्छेद करती है। तो दर्शाइए कि
ar (BPC) = ar (DPQ) है।
हल :
दिया है: ABCD एक समान्तर चतुर्भुज है। BC को बिन्दु 9 तक इस प्रकार बढ़ाया D८ गया है कि AD = CQ। रेखाखण्ड AQ को मिलाया गया है जो DC को बिन्दु P पर प्रतिच्छेद करता है।
सिद्ध करना है : ar (BPC) = ar (DPQ)
उपपत्ति : ABCD एक समान्तर चतुर्भुज है।
AD = BC और दिया है कि AD = CQ
BC = CQ अर्थात C, BQ का मध्य-बिन्दु है।
PC, ∆PBQ की माध्यिका है।
ar (∆BPC) = ar (∆PCQ)
AD = CQ और AD || CQ (AD || BC)
ADQC एक समान्तर चतुर्भुज है जिसके विकर्ण AQ तथा CD हैं।
P, CD का मध्य-बिन्दु है या PQ, ∆DQC की माध्यिका है।
ar (DPR) = ar (PCQ)
तब समीकरण (1) व (2) से,
ar (BPC) = ar (DPQ)
Proved.
प्रश्न 5.
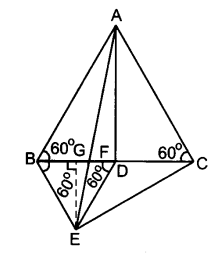
दी गई आकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिन्दु है। यदि AE भुजा BC को F पर प्रतिच्छेद करती है तो दर्शाइए कि
(i) ar (BDE) =
(ii) ar (BDE) =
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 
हल :
दिया है : दी गई आकृति ∆ABC और ∆BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिन्दु है। रेखाखण्ड AE, खींचा गया है जो BC को F पर प्रतिच्छेद करता है। सिद्ध करना है :
(i) ar (BDE) =
(ii) ar (BDE) =
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) =
उपपत्ति (i) D, BC का मध्य-बिन्दु है।
BD = DC
BD =
प्रश्न 6.
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते हैं। दर्शाइए कि ar (APB) x ar (CPD) = ar (APD) x ar (BPC) है।
हल :
दिया है : ABCD के विकर्ण AC और BD हैं जो परस्पर बिन्दु P पर प्रतिच्छेद करते हैं।
सिद्ध करना है: ar (APB) x ar (CPD) = ar (APD) x ar (BPC)
रचना : A तथा C से BD पर क्रमशः AM व CN लम्ब खींचे।
प्रश्न 7.
P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिन्दु हैं तथा रेखाखण्ड AP का मध्य-बिन्दु है। दर्शाइए कि :
(i) ar (PRQ) =
(ii) ar (RQC) = 
प्रश्न 8.
दी गई आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः भुजाओं BC, CA और AB पर बने वर्ग हैं। रेखाखण्ड AX ⊥ DE भुजा BC को बिन्दु Y पर मिलता है। दर्शाइए कि :
(i) ∆MBC = ∆ABD
(ii) ar (BYXD) = 2 ar (MBC)
(iii) ar (BYXD) = ar (ABMN)
(iv) ∆FCB = ∆ACE
(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
हल :
दिया है : ∆ABC में ∠A समकोण है। त्रिभुज की भुजाओं AB, AC तथा BC पर क्रमश: ABMN, ACFG और BCED वर्ग बने हैं। रेखाखण्ड AX वर्ग BCED की भुजा DE पर लम्ब है, जो BC से Y पर मिलता है।
सिद्ध करना है :
(i) ∆MBC = ∆ABD
(ii) ar (BYXD) = 2 ar (MBC)
(iii) ar (BYXD) = ar (ABMN)
(iv) ∆FCB = ∆ACE
(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
