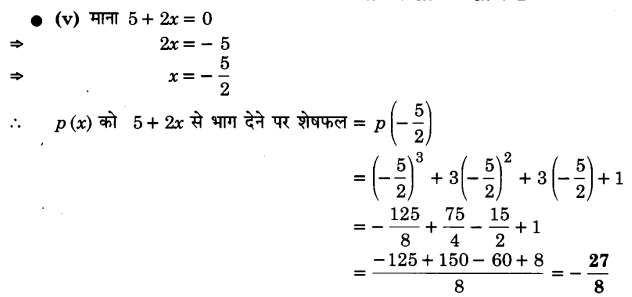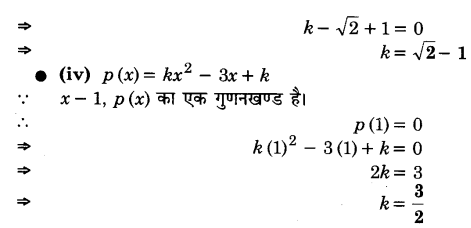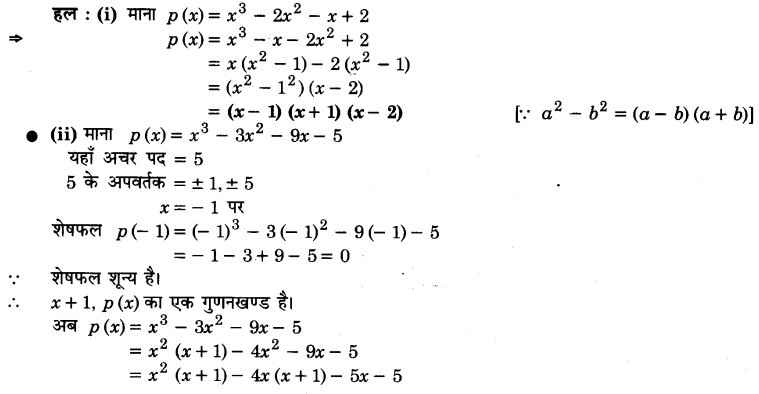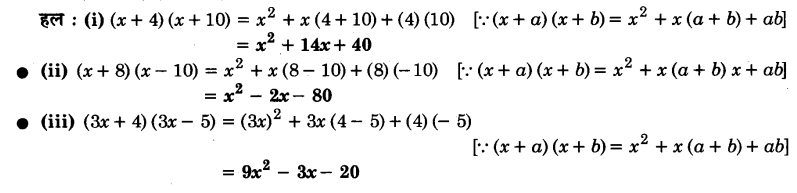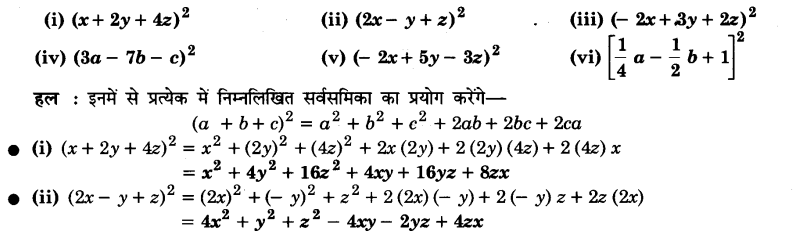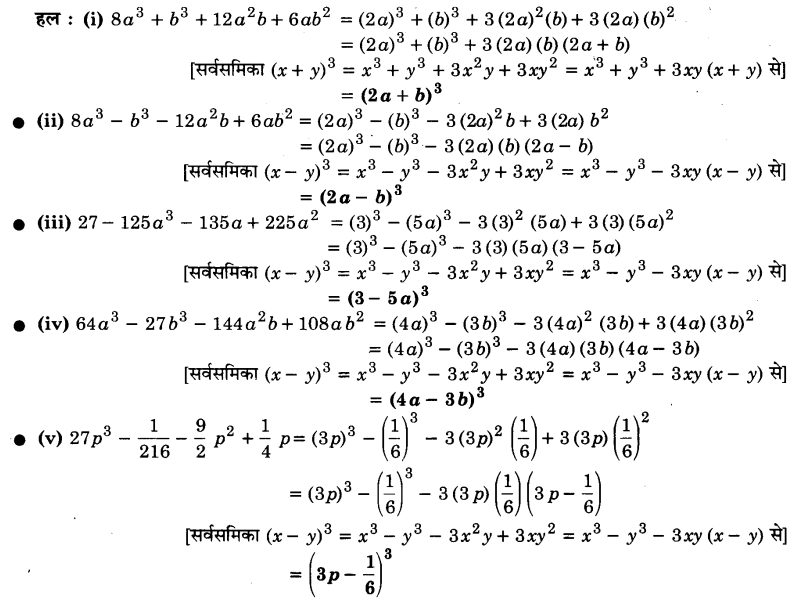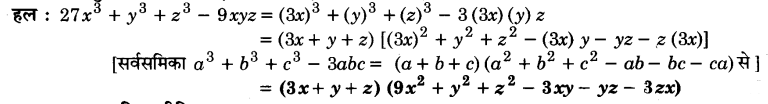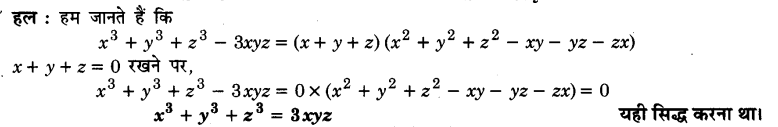NCERT Solutions Class 9 गणित Chapter-2 (बहुपद)
Class 9 गणित
पाठ-2 (बहुपद)
अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर
प्रश्नावली 2.1
प्रश्न 1.
निम्नलिखित व्यंजकों में कौन-कौन एक चर में बहुपद हैं और कौन-कौन नहीं हैं? कारण के साथ अपने उत्तर दीजिए :
प्रश्न 2.
निम्नलिखित में से प्रत्येक में x² का गुणांक लिखिए :
(i) 2 + x² + x
(ii) 2 – x² + x3
(iii) x² + x
(iv) √2 x – 1
हल :
(i) 2 + x² + x में x² का गुणांक = 1
(ii) 2 – x² + x3 में x² का गुणांक = -1
(iii) x² + x में x² का गुणांक =
(iv) √2 x – 1 अर्थात 0.x2 + √2 x – 1 में x² का गुणांक = 0
प्रश्न 3.
35 घात के द्विपद का और 100 घात के एकपदी का एक-एक उदाहरण दीजिए।
प्रश्न 4.
निम्नलिखित बहुपदों में से प्रत्येक बहुपद की घात लिखिए :
(i) 5x3 + 4x² + 7x
(ii) 4 – y²
(iii) 5t – √7
(iv) 3
हल :
(i) 5x3 + 4x² + 7x में चर x की अधिकतम घात = 3
दिए हुए बहुपद की घात= 3
(ii) 4 – y² में चर y की अधिकतम घात = 2
दिए हुए बहुपद की घात = 2
(iii) 5t – √7 में चर है की अधिकतम घात = 1
दिए हुए बहुपद की घात = 1
(iv) 3 एक अचर पद है अर्थात 3.x0
दिए हुए बहुपद की घात = 0
प्रश्न 5.
बताइए कि निम्नलिखित बहुपदों में कौन-कौन बहुपद रैखिक है, कौन-कौन द्विघाती हैं और कौन-कौन त्रिघाती हैं :
(i) x² + x
(ii) x – x3
(iii) y + y² + 4
(iv) 1 + x
(v) 3t
(vi) r²
(vii) 7x3
हल :
(i) बहुपद x² + x में चर x की अधिकतम घात = 2
यह बहुपद द्विघाती है।
(ii) बहुपद x – x3 में चर x की अधिकतम घात = 3
यह बहुपद त्रिघाती है।
(iii) बहुपद y + y² + 4 में चर y की अधिकतम घात = 2
यह बहुपद द्विघाती है।
(iv) बहुपद 1 + x में चर x की अधिकतम घात 1 है।
यह बहुपद रैखिक है।
(v) बहुपद 3t में चर है की अधिकतम घात 1 है।
यह बहुपद रैखिक है।
(vi) बहुपद r² में चर r की अधिकतम घात 2 है।
यह बहुपद द्विघाती है।
(vii) बहुपद 7x3 में चर x की अधिकतम घात 3 है।
यह बहुपद त्रिघाती है।
प्रटनावली 2.2
प्रश्न 1.
निम्नलिखित पर बहुपद 5x – 4x² + 3 के मान ज्ञात कीजिए।
(i) x = 0
(ii) x = – 1
(iii) x = 2
हल :
माना बहुपद p (x) = 5 – 4x² + 3
(i) x = 0 पर बहुपद p (x) का मान
p(0)= 5 (0) – 4 (0)² + 3 = 3
(ii) x = -1 पर बहुपद p (x) का मान
p(-1) = 5 (-1) – 4 (-1)² + 3 = – 5 – 4 + 3 = -6
(iii) x = 2 पर बहुपद p (x) का मान
p(2) = 5 (2) – 4 (2)2 + 3 = 10 – 16 + 3 = -3
प्रश्न 2.
निम्नलिखित बहुपदों में से प्रत्येक बहुपद के लिए p (0), p (1) और p (2) ज्ञात कीजिए :
(i) p(y) = y² – y + 1
(ii) p(t) = 2 + t + 2t² – t3
(iii) p(x) = x3
(iv) p(x) = (x – 1)(x + 1)
हल :
(i) p(y) = y² – y + 1
p (0) = 0² – 0 + 1 = 0 – 0 + 1 = 1
p (1) = 1² – 1 + 1 = 1 – 1 + 1 = 1
p(2) = 2² – 2 + 1 = 4 – 2 + 1 = 3
(ii) p(t) = 2 + t + 2t² – t3
p(0) = 2 + 0 + 2 (0)² – (0)3 = 2
p (1) = 2 + 1 + 2 (1)² – (1)3 = 2 + 1 + 2 – 1 = 4
p (2) = 2 + 2 + 2 (2)² – (2)3 = 2 + 2 + 8 – 8 = 4
(iii) p (x) = x3
p(0) = (0)3 = 0
p (1) = (1)3 = 1
p (2) = (2)3 = 8
(iv) p (x) = (x – 1) (x + 1)
p(0) = (0 – 1) (0 + 1) = (-1) (1) = -1
p (1) = (1 – 1) (1 + 1) = (0) (2) = 0
p (3) = (2 – 1) (2 + 1) = (1) (3) = 3
प्रश्न 3.
सत्यापित कीजिए कि दिखाए गए मान निम्नलिखित स्थितियों में संगत बहुपद के शून्यक हैं :
प्रश्न 4.
निम्नलिखित स्थितियों में से प्रत्येक स्थिति में बहुपद को शून्यक ज्ञात कीजिए :
(i) p(x) = x + 5
(ii) p(x) = x – 5
(iii) p(x) = 2x + 5
(iv) p(x) = 3x – 2
(v) p(x) = 3x
(vi) p(x) = ax; a ≠ 0
(vii) p (x) = cx + d; c ≠ 0, c, d वास्तविक संख्याएँ हैं।
हल :
(i) बहुपद p (x) = x + 5 का शून्यक ज्ञात करने के लिए इसे शून्य के बराबर रखते हैं।
p(x) = 0
⇒ x + 5 = 0
⇒ x = – 5
p(3) को शून्यक = – 5
(ii) बहुपद p (x) = x – 5 को शून्यक ज्ञात करने के लिए इसे शून्य के बराबर रखते हैं।
p (x) = 0
⇒ x – 5 = 0
⇒ x = 5
p(x) का शून्यक = 5
(iii) बहुपद p (x) = 2x + 5 का शून्यक ज्ञात करने के लिए इसे शून्य के बराबर रखते हैं।
p(3) = 0
⇒ 2x + 5 = 0
⇒ 2x = – 5
⇒ x =
p (x) का शून्यके =
(iv) बहुपद p (x) = 3x – 2 का शून्यक ज्ञात करने के लिए इसे शून्य के बराबर रखते हैं।
p (5) = 0
⇒ 3x – 2 = 0
⇒ 3x = 2
⇒ x =
p (x) का शून्यक =
(v) बहुपद p (x) = 3x का शून्यक ज्ञात करने के लिए इसे शून्य के बराबर रखते हैं।
p (x) = 0
⇒ 3x = 0
⇒ x = 0
p (x) का शून्यक = 0
(vi) बहुपद p(x) = ax; a ≠ 0 का शून्यक ज्ञात करने के लिए इसे शून्य के बराबर रखते हैं।
p(x) = 0
⇒ ax = 0
⇒ x = 0 (a ≠ 0)
p(x) का शून्यक = 0
(vii) बहुपद p (x) = cx + d, c ≠ 0 का शून्यक ज्ञात करने के लिए इसे शून्य के बराबर रखते हैं।
p(x) = 0
cx + d = 0
cx = -d
x = (c ≠ 0)
p (x) का शून्यक =
प्रश्नावली 2.3
प्रश्न 1.
x3 + 3x² + 3x + 1 को निम्नलिखित से भाग देने पर शेषफल ज्ञात कीजिए :
(i) x + 1
(ii) x –
(iii) x
(iv) x + π
(v) 5 + 2x
हल :
माना p (x) = x3 + 3x² + 3x + 1
(i) माना x + 1 = 0 ⇒ x = -1
p (x) को + 1 से भाग देने पर शेषफल
p(- 1) = (-1)3 + 3(-1)² + 3(-1) + 1 = -1 + 3 – 3 + 1 = 0
प्रश्न 2.
x3 – ax² + 6x – a को x – a से भाग देने पर शेषफल ज्ञात कीजिए।
हल :
माना p (x) = x3 – ax² + 6x – a तथा x – a = 0
p (x) को x – a से भाग देने पर शेषफल = (a)3 – a(a)² + 6(a) – a = a3 – a3 + 6a – a = 5a
प्रश्न 3.
जाँच कीजिए कि 7 + 3x, 3x3 + 7x का एक गुणनखण्ड है या नहीं।
हल :
माना p (x) = 3x + 7x
यदि 7 + 3x, p (x) का एक गुणनखण्ड है तो p (x) को 7 + 3x से भाग देने पर शेषफल शून्य होना चाहिए।
माना 7 + 3x = 0 ⇒ 3x = – 7 ⇒ x =
प्रश्नावली 2.4
प्रश्न 1.
बताइए कि निम्नलिखित बहुपदों में से किस बहुपद का एक गुणनखण्ड (x + 1) है।
(i) x3 + x2 + x + 1
(ii) x4 + x3 + x2 + x + 1
(iii) x4 + 3x3 + 3x2 + x + 1
(iv) x3 – x2 – (2 + √2) x + √2
प्रश्न 2.
गुणनखण्ड प्रमेय लागू करके बताइए कि निम्नलिखित स्थितियों में से प्रत्येक स्थिति में g (x), p (x) का एक गुणनखण्ड है या नहीं :
(i) p(x) = 2x3 + x2 – 2x – 1, g (x) = x + 1
(ii) p(x) = x3 + 3x2 + 3x + 1, g (3) = x + 2
(iii) p(x) = x3 – 4x2 + x + 6, g (x) = x – 3
प्रश्न 3.
k का मान ज्ञात कीजिए जबकि निम्नलिखित स्थितियों में से प्रत्येक स्थिति में (x – 1), p (x) का एक गुणनखण्ड हो :
(i) p(3) = x2 + x + k
(ii) p(x) = 2x2 + kx + √2
(iii) p(x) = kx2 – √2 x + 1
(iv) p(x) = kx2 – 3x + k
प्रश्न 4.
गुणनखण्ड ज्ञात कीजिए :
(i) 12x2 – 7x + 1
(ii) 2x2 + 7x + 3
(iii) 6x2 + 5x – 6
(iv) 3x2 – x – 4
प्रश्न 5.
गुणनखण्ड ज्ञात कीजिए :
(i) x3 – 2x2 – x + 2
(ii) x3 – 3x2 – 9x – 5
(iii) x3 + 13x2 + 32x + 20
(iv) 2y3 + y2 – 2y – 1
प्रश्नावली 2.5
प्रश्न 1.
उपयुक्त सर्वसमिकाओं को प्रयोग करके निम्नलिखित गुणनफल ज्ञात कीजिए :
(i) (x + 4) (x + 10)
(ii) (x + 8) (x – 10)
(iii) (3x + 4) (3x – 5)
(iv) (y2 + ) (y2 –
)
(v) (3 – 2x) (3 + 2x)
प्रश्न 2.
सीधे गुणा किए बिना निम्नलिखित गुणनफलों के मान ज्ञात कीजिए :
(i) 103 x 107
(ii) 95 x 96
(iii) 104 x 96
प्रश्न 3.
उपयुक्त सर्वसमिकाएँ प्रयोग करके निम्नलिखित का गुणनखण्डन कीजिए :
(i) 9x2 + 6xy + y2
(ii) 4y2 – 4y + 1
(iii) x2 –
प्रश्न 4.
उपयुक्त सर्वसमिकाओं का प्रयोग करके निम्नलिखित में से प्रत्येक का प्रसार कीजिए :
प्रश्न 5.
गुणनखण्डन कीजिए :
प्रश्न 6.
निम्नलिखित घनों को प्रसारित रूप में लिखिए :
प्रश्न 7.
उपयुक्त सर्वसमिकाएँ प्रयोग करके निम्नलिखित के मान ज्ञात कीजिए :
(i) (99)3
(ii) (102)3
(iii) (998)3
प्रश्न 8.
निम्नलिखित में से प्रत्येक का गुणनखण्डन कीजिए।
प्रश्न 9.
सत्यापित कीजिए :
प्रश्न 10.
निम्नलिखित में से प्रत्येक का गुणनखण्डन कीजिए
प्रश्न 11.
गुणनखण्ड कीजिए : 27x3 + y3 + z3 – 9xyz
प्रश्न 12.
सत्यापित कीजिए :
प्रश्न 13.
यदि x + y + z = 0 हो तो दिखाइए कि x3 + y3 + z3 = 3xyz
प्रश्न 14.
घनों का परिकलन किए बिना निम्नलिखित में से प्रत्येक का मान ज्ञात कीजिए :
प्रश्न 15.
नीचे दिए गए आयतों, जिनमें उनके क्षेत्रफल दिए गए हैं, में से प्रत्येक की लम्बाई और चौड़ाई के लिए सम्भव व्यंजक दीजिए।
(i) क्षेत्रफल : 25a2 – 35a + 12
(ii) क्षेत्रफल : 35y2 + 13y – 12
प्रश्न 16.
घनाभों (Cuboids), जिनके आयतन नीचे दिए गए हैं, की विमाओं के लिए सम्भव व्यंजक क्या हैं :
(i) आयतन : 3x2 – 12x
(ii) आयतन : 12ky2 + 8ky – 20k