NCERT Solutions Class 9 गणित Chapter-10 (वृत्त)

NCERT Solutions Class 9  गणित 9 वीं कक्षा से Chapter-10 (वृत्त) के उत्तर मिलेंगे। यह अध्याय आपको मूल बातें सीखने में मदद करेगा और आपको इस अध्याय से अपनी परीक्षा में कम से कम एक प्रश्न की उम्मीद करनी चाहिए। 

हमने NCERT बोर्ड की टेक्सटबुक्स हिंदी गणित के सभी Questions के जवाब बड़ी ही आसान भाषा में दिए हैं जिनको समझना और याद करना Students के लिए बहुत आसान रहेगा जिस से आप अपनी परीक्षा में अच्छे नंबर से पास हो सके।

एनसीईआरटी प्रश्न-उत्तर

Class 9 गणित

पाठ-10 (वृत्त)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्नावली 10.1

प्रश्न 1.

खाली स्थान भरिए।

(i) वृत्त का केन्द्र वृत्त के ……………….. में स्थित है (बहिर्भाग/अभ्यन्तर)।

(ii) एक बिन्दु, जिसकी वृत्त के केन्द्र से दूरी त्रिज्या से अधिक हो, वृत्त के ………… में स्थित होता है (बहिर्भाग/अभ्यन्तर)।

(iii) वृत्त की सबसे बड़ी जीवा वृत्त का ……………… होती है।

(iv) एक चाप ………………… होता है, जब इसके सिरे एक व्यास के सिरे हों।

(v) वृत्तखण्ड एक चाप तथा ……………….. के बीच का भाग होता है।

(vi) एक वृत्त, जिस तल पर स्थित है, उसे ………………….. भागों में विभाजित करता है।

हल :

(i) वृत्त का केन्द्र वृत्त के अभ्यन्तर में स्थित होता है।

(ii) एक बिन्दु, जिसकी वृत्त के केन्द्र से दूरी त्रिज्या से अधिक हो, वृत्त के बहिर्भाग में स्थित होता है।

(iii) वृत्त की सबसे बड़ी जीवा वृत्त का व्यास होती है।

(iv) एक चाप अर्धवृत्त होता है, जब इसके सिरे एक व्यास के सिरे हों।

(v) वृत्तखण्ड एक चाप तथा जीवा के बीच का भाग होता है।

(vi) एक वृत्त, जिस तल पर स्थित है, उसे तीन भागों में विभाजित करता है।

प्रश्न 2.

लिखिए, सत्य या असत्य। अपने उत्तर के कारण दीजिए।

(i) केन्द्र को वृत्त पर किसी बिन्दु से मिलाने वाला रेखाखण्ड वृत्त की त्रिज्या होती है।

(ii) एक वृत्त में समान लम्बाई की परिमित जीवाएँ होती हैं।

(iii) यदि एक वृत्त को तीन बराबर चापों में बाँट दिया जाए, तो प्रत्येक भाग दीर्घ चाप होता है।

(iv) वृत्त की एक जीवा, जिसकी लम्बाई त्रिज्या से दो गुनी हो, वृत्त का व्यास है।

(v) त्रिज्यखण्ड, जीवा एवं संगत चाप के बीच का क्षेत्र होता है।

(vi) वृत्त एक समतल आकृति है।

हल :

(i) केन्द्र को वृत्त पर किसी बिन्दु से मिलाने वाला रेखाखण्ड वृत्त की त्रिज्या होती है’ कथन सत्य है।

(ii) एक वृत्त में समान लम्बाई की परिमित जीवाएँ होती हैं कथन असत्य है क्योंकि किसी वृत्त में समान लम्बाई की अपरिमित जीवाएँ होती हैं।

(iii) यदि एक वृत्त को तीन बराबर चापों में बाँट दिया जाए, तो प्रत्येक भागे दीर्घ चाप होता है’ कथन असत्य है। क्योंकि वृत्त के आधे से कम भाग को अन्तरित करने वाला चाप लघु चाप होता है।

(iv) ‘वृत्त की एक जीवा, जिसकी लम्बाई त्रिज्या से दो गुनी हो, वृत्त का व्यास है।’ कथन सत्य है।

(v) ‘त्रिज्यखण्ड, जीवा एवं संगत चाप के बीच का क्षेत्र होता है।’ कथन असत्य है।

(vi) ‘वृत्त एक समतल आकृति है’ कथन सत्य है।

प्रश्नावली 10.2

प्रश्न 1.

याद कीजिए कि दो वृत्त सर्वांगसम होते हैं, यदि उनकी त्रिज्याएँ बराबर हों। सिद्ध कीजिए कि सर्वांगसम वृत्तों की बराबर जीवाएँ उनके केन्द्रों पर बराबर कोण अन्तरित करती हैं।

हल :

दिया है : केन्द्र O वाला एक वृत्त है जिसकी एक जीवा AB है।

केन्द्र O वाला एक अन्य वृत्त है जिसकी एक जीवा CD है। दोनों वृत्त सर्वांगसम हैं और जीवा AB जीवा CD के बराबर है।

जीवा AB केन्द्र O पर ∠ AOB तथा जीवा CD केन्द्र O’ पर ∠ CO’D अन्तरित करती है।

सिद्ध करना है : ∠AOB = ∠COD

रचना : त्रिज्याएँ OA, OB, O’C व O’D खींचिए।

उपपत्ति: ∆AOB तथा ∆CO’D में,

AB = CD (दिया है।)

OA = O’C (सर्वांगसम वृत्तों की त्रिज्याएँ बराबर होती हैं।)

OB = O’D (सर्वांगसम वृत्तों की त्रिज्याएँ बराबर होती हैं)

∆AOB = ∆COD (S.S.S. से)

∠AOB = ∠COD (C.P.C.T.)

Proved.

प्रश्न 2.

सिद्ध कीजिए कि यदि सर्वांगसम वृत्तों की जीवाएँ उनके केन्द्रों पर बराबर कोण अन्तरित करें, तो जीवाएँ बराबर होती हैं।

हल :

दिया है : O तथा O’ केन्द्रों वाले दो सर्वांगसम वृत्त हैं। जिनकी जीवाएँ AB व CD उनके केन्द्रों O तथा O’ पर क्रमशः ∠AOB व ∠CO’D

इस प्रकार अन्तरित करती हैं कि ∠AOB = ∠ CO’D है।

सिद्ध करना है : जीवा AB = जीवा CD

उपपत्ति: ∆AOB और ∆CO’D में,

OA = O’C (सर्वांगसम वृत्तों की त्रिज्याएँ बराबर होती हैं।)

∠AOB = ∠ COD (दिया है।)

OB = O’D (सर्वांगसम वृत्तों की त्रिज्याएँ बराबर होती हैं।)

∆AOB = ∆COD (S.A.S. से)

AB = CD (C.P.C.T.)

अतः जीवा AB = जीवा CD

Proved.

प्रश्नावली 10.3

प्रश्न 1.

वृत्तों के कई युग्म (जोड़े) खींचिए। प्रत्येक जोड़े में कितने बिन्दु उभयनिष्ठ हैं? उभयनिष्ठ बिन्दुओं की अधिकतम संख्या क्या है?

हल :

प्रश्न के निर्देश के अनुसार नीचे विभिन्न वृत्तों के युग्म खींचे गए हैं। इन्हें ध्यान से देखिए :

दोनों युग्मों में कोई बिन्दु उभयनिष्ठ नहीं है।

दोनों युग्मों में केवल एक बिन्दु उभयनिष्ठ है।

प्रत्येक युग्म में दो बिन्दु उभयनिष्ठ हैं। अतः दो वृत्तों के उभयनिष्ठ बिन्दु की अधिकतम संख्या = 2

प्रश्न 2.

मान लीजिए आपको एक वृत्त दिया है। एक रचना इसके केन्द्र को ज्ञात करने के लिए दीजिए।

हल :

दिया है : अज्ञात केन्द्र वाला एक वृत्त।। ज्ञात करना है : वृत्त का केन्द्र।

रचना :

(1) वृत्त की परिधि पर तीन बिन्दु A, B व C लिए।

(2) जीवाएँ AB व BC खींचीं।

(3) जीवा AB व जीवा BC दोनों के लम्ब समद्विभाजक खींचे जो परस्पर बिन्दु O पर काटते हैं।

बिन्दु O वृत्त का अभीष्ट केन्द्र है।

प्रश्न 3.

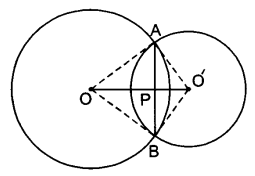
यदि दो वृत्त परस्पर दो बिन्दुओं पर प्रतिच्छेद करें, तो सिद्ध कीजिए कि उनके केन्द्र उभयनिष्ठ जीवा के लम्ब-समद्विभाजक पर स्थित हैं।

हल :

दिया है : O तथा O’ केन्द्र वाले दो वृत्त हैं जो परस्पर दो बिन्दुओं A तथा B पर प्रतिच्छेद करते हैं। AB वृत्तों की उभयनिष्ठ जीवा है और OO’ उनके केन्द्रों को मिलाने वाली रेखा है। AB और OO’ एक-दूसरे को बिन्दु P पर काटते हैं।

सिद्ध करना है : OO’, AB का लम्ब समद्विभाजक है।

रचना : वृत्तों की त्रिज्याएँ OA, OB, O’A व O’B खींचीं।

उपपत्ति: ∆OAO’ तथा ∆OBO’ में,

OA = OB (एक ही वृत्त की त्रिज्याएँ बराबर होती हैं।)

O’A= O’B (एक ही वृत्त की त्रिज्याएँ बराबर होती हैं।)

OO’ = OO’ (उभयनिष्ठ भुजा है)

Δ ΟΑΟ’ = Δ ΟΒΟ’ (S.S.S. से)

∆AOO’ = ∆BOO’ या

∠AOP = ∠ BOP (C.P.C.T.)

तब ∆AOP और ∆BOP में,

OA = OB (एक ही वृत्त की त्रिज्याएँ बराबर होती हैं।)

∠ AOP = ∠ BOP (ऊपर सिद्ध किया है।)

OP = OP (उभयनिष्ठ भुजा है)

∆AOP = ∆BOP

AP = BP और ∠OPA = ∠OPB

AP = BP;

अत: OO’ बिन्दु P पर AB को समद्विभाजित करता है। :

∠OPA = ∠OPB और APB एक रेखा (उभयनिष्ठ जीवा) है।

∠OPA + ∠OPB = 180°

हल करने पर, ∠OPA = 90° व ∠OPB = 90°

अतः OO” उभयनिष्ठ जीवा AB का लम्ब-समद्विभाजक है।

प्रश्नावली 10.4

प्रश्न 1.

5 सेमी और 3 सेमी त्रिज्या वाले दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं तथा उनके केन्द्रों के बीच की दूरी 4 सेमी है। उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए।

हुल :

दिया है: O तथा O’ केन्द्रों वाले वृत्तों की त्रिज्याएँ OA तथा O’A क्रमशः 5 सेमी व 3 सेमी हैं।

उनके केन्द्रों के बीच की दूरी OO’ = 4 सेमी है।

ज्ञात करनी है : उभयनिष्ठ जीवा AB की माप। गणना

∆OAO’ की भुजाएँ O’A = 3 सेमी,

OO’ = 4 सेमी व OA = 5 सेमी हैं।

तब, OA² = (25) और O’A² +(OO’)² = (3)² + (4)² = 25

OA² = O’A² + OO’² (पाइथागोरस प्रमेय से)

अतः ∆OAO’ समकोणीय है।

∠ AOO’ = 90°

परन्तु APB उभयनिष्ठ जीवा है जो OO” पर लम्ब होना चाहिए।

अतः P और O’ एक ही बिन्दु है अर्थात्

त्रिज्या AO’ = उभयनिष्ठ जीवा का भाग AP

उभयनिष्ठ जीवा का भाग AP = AO’ = 3 सेमी

केन्द्र रेखा OO’ उभयनिष्ठ जीवा AB की लम्ब-समद्विभाजक होगी।

AB = 2 x AP = 2 x 3 = 6 सेमी

अत: उभयनिष्ठ जीवा की लम्बाई = 6 सेमी।

प्रश्न 2.

यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खण्ड दूसरी जीवा के संगत खण्डों के बराबर हैं।

हल :

दिया है : O केन्द्र वाले एक वृत्त की AB व CD दो बराबर जीवाएँ हैं जो एक-दूसरे को वृत्त के अन्दर बिन्दु P पर काटती हैं।

सिद्ध करना है : AP = CP तथा BP = DP

रचना : वृत्त के केन्द्र O से जीवा AB पर OM तथा जीवा CD पर ON लम्बे खींचे।। रेखाखण्ड OP खींचा।

उपपत्ति : OM ⊥ AB ⇒ ∠OMP = 90°

और ON ⊥ CD ⇒ ∠ONP = 90°

∆OMP और ∆ONP समकोणीय हैं।

तब, समकोण ∆OMP तथा ∆ONP में,

OM = ON (जीवा AB = जीवा CD)

OP = OP (उभयनिष्ठ जीवा है।)

∠OMP = ∠ONP (प्रत्येक 90°)

∆OMP = ∆ONP (R.H.S. से)

MP = NP (C.P.C.T.) …(1)

OM ⊥ AB

AM = BM

AP + PM = BM

AP = BM – PM

AP = AB – PM (∵ AM = BM = ) …..(2)

और ON ⊥ CD

CN = DN

CP + PN = DN

CP = DN – PN

CP = CD – PN (CN = DN = )
CP = AB – PM [CD = AB तथा समीकरण (1) से PN = PM] …(3)

अब समीकरण (2) व (3) से,

AP = CP

AB = CD (दिया है।)

AP + BP = CP + DP (चित्र से) परन्तु

AP = CP (ऊपर सिद्ध किया है।)

घटाने पर BP = DP

अत: AP = CP और BP = DP

अर्थात एक जीवा AB के खण्ड दूसरी जीवा CD के संगत खण्डों के बराबर हैं।

Proved.

प्रश्न 3.

यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें तो सिद्ध कीजिए कि प्रतिच्छेद बिन्दु को केन्द्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती है।

हल :

दिया है : केन्द्र O के वृत्त की दो बराबर जीवाएँ AB और CD जो बिन्दु P पर प्रतिच्छेदन करती हैं।

सिद्ध करना है: रेखाखण्ड OP, से जीवाओं AB व CD द्वारा बने ∠BPO = ∠DPO

रचना : केन्द्र O से AB और CD पर क्रमशः OM और ON लम्ब डाले।

उपपत्ति : जीवा AB = जीवा CD

OM = ON

अब ΔOPM और ΔOPN में,

OM = ON (दिया है।)

∠OMP = ∠ONP (प्रत्येक समकोण है।)

OP = OP (उभयनिष्ठ भुजा है।)

ΔOPM = ΔOPN (R.H.S. से)

अतः ∠MPO = NPO यो ∠BPO = ∠DPO (C.P.C.T.)

Proved.

प्रश्न 4.

यदि एक रेखा दो संकेन्द्रीय वृत्तों (एक ही केन्द्र वाले वृत्त) को, जिनका केन्द्र O है, A, B, C और D पर प्रतिच्छेद करे, तो सिद्ध कीजिए AB = CD है।

हल :

दिया है : दो संकेन्द्रीय वृत्तों का केन्द्र 0 है। एक ऋजु रेखा वृत्तों को बिन्दुओं A, B, C और D पर प्रतिच्छेदित करती है।

सिद्ध करना है : AB = CD

रचना : वृत्त के केन्द्र O से हैं पर OM लम्ब डाला।

उपपत्ति : रेखा l बड़े वृत्त को बिन्दुओं A तथा D पर काटती है।

AB वृत्त की जीवा है और OM उस पर केन्द्र से डाला गया लम्ब है।

AM = MD ……..(1)

रेखा l छोटे वृत्त को बिन्दुओं B तथा C पर काटती है।

BC वृत्त की जीवा है और OM उस पर केन्द्र से खींचा गया लम्ब है।

BM = MC ……..(2)

समीकरण (1) में से (2) को घटाने पर,

AM – BM = MD – MC

अतः AB = CD

Proved.

प्रश्न 5.

एक पार्क में बने 5 मीटर त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 मीटर हो तो रेशमा और मनदीप के बीच की दूरी क्या है?

हल :

दिया है। एक पार्क में 5 मीटर त्रिज्या का एक वृत्त बना है जिसका केन्द्र O है। तीन लड़कियाँ रेशमा, सलमी और मनदीप वृत्त पर क्रमशः A, B व C स्थानों पर खड़ी हैं। रेशमा और सलमा के बीच की दूरी AB = 6 मीटर तथा सलमा और मनदीप के बीच दूरी BC = 6 मीटर है।

ज्ञात करना है : रेशमा और मनदीप के बीच की दूरी = AC

गणना : त्रिज्याएँ OA और OB खींचीं और माना कि OB, AC को बिन्दु P पर काटती है।

ΔOAB में, OA = 5 मीटर (त्रिज्या), OB = 5मीटर (त्रिज्या) तथा AB = 6 मीटर।

माना OA = 5 मीटर = a, OB = 5 मीटर = b और AB = 6 मीटर = c अर्धपरिमाप

प्रश्न 6.

20 मीटर त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कॉलोनी में स्थित है। तीन लड़के अंकुर, सैय्यद तथा डेविड इसकी परिसीमा पर बराबर दूरी पर बैठे हैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक फोन की डोरी की लम्बाई ज्ञात कीजिए।

हल :

दिया है : O केन्द्र वाला एक वृत्त के आकार का पार्क है जिसकी त्रिज्या OA या OB = 20 मीटर है। वृत्त की परिधि पर तीन लड़के एक-दूसरे से बराबर दूरी पर A, B व C स्थानों पर ऐसे बैठे हैं कि

AB = BC = AC

प्रश्नावली 10.5

प्रश्न 1.

केन्द्र O वाले एक वृत्त पर तीन बिन्दु A, B और C इस प्रकार हैं कि ∠BOC = 30° तथा ∠AOB = 60° है। यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिन्दु है तो ∠ADC ज्ञात कीजिए।

हल :

दिया है : O केन्द्र वाला एक वृत्त है जिसकी परिधि पर A, B और C तीन बिन्दु इस प्रकार हैं कि ∠AOB = 60° और ∠ BOC = 30° हैं।

चाप ABC के अतिरिक्त वृत्त की परिधि पर एक बिन्दु D है जो चाप ABC के साथ ∠ ADC बनाता है।

ज्ञात करना है: ∠ADC गणना : ∠AOB = 60° और ∠BOC = 30°

जोड़ने पर, ∠AOB + ∠ BOC = 60° + 30°= 90°

∠ AOC = 90°

∠AOC, चाप ABC द्वारा केन्द्र पर बना कोण है।

वृत्त की शेष परिधि पर चाप ABC द्वारा बना कोण ∠ADC, ∠AOC का आधा होगा।

∠ADC = ∠AOC = x 90° = 45°
∠ADC = 45°

प्रश्न 2.

किसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी बिन्दु पर अन्तरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिन्दु पर भी अन्तरित कोण ज्ञात कीजिए।

हल:

दिया है। एक वृत्त का केन्द्र 0 है। उसकी एक जीवा AB वृत्त की त्रिज्या OA के बराबर है। वृत्त के लघु चाप ACB पर एक बिन्दु C तथा दीर्घ चाप ADB पर एक बिन्दु D है। चाप ACB द्वारा बिन्दु D पर अन्तरित ∠ADB तथा चाप ADB द्वारा बिन्दु C पर अन्तरित ∠ACB है।

ज्ञात करना है : ∠ACB व ∠ADB

विश्लेषण व गणना :

जीवा AB = वृत्त की त्रिज्या OA या OB

AB = OA = OB

ΔABC समबाहु त्रिभुज है।

∠AOB = 60° जो चाप ACB द्वारा केन्द्र पर अन्तरित कोण है। :

चाप ACB द्वारा वृत्त की शेष परिधि के बिन्दु D पर अन्तरित ∠ADB = ∠AOB

∠ADB = x ADB
= x 60° = 30°
इसी प्रकार, चाप ADB द्वारा वृत्त के केन्द्र O पर अन्तरित वृहत्कोण AOB = 360° – 60° = 300°
तब चाप ADB द्वारा वृत्त की शेष परिधि के बिन्दु C पर अन्तरित कोण ।
∠ACB = वृहत्कोण ∠AOB = x 30° = 150°
अतः ∠ACB = 150° तथा ∠ADB = 30°

प्रश्न 3.

∠PQR = 100° है, जहाँ P, Q तथा R, केन्द्र O वाले एक वृत्त पर स्थित Q बिन्दु हैं। ∠OPR ज्ञात कीजिए।

हल :

दिया है : O केन्द्र का एक वृत्त है जिसकी परिधि पर P, Q व R तीन बिन्दु हैं।

ज्ञात करना है : ∠OPR

गणना : दीर्घ चाप PR द्वारा वृत्त के केन्द्र पर बना कोण वृहत्कोण ∠POR है और इस चाप द्वारा शेष परिधि PQR के बिन्दु Q पर बना ∠PQR है।

∠PQR  = x वृहत्कोण ∠POR

100°  = वृहत्कोण ∠POR

वृहत्कोण ∠ POR = 200°

तब, शेष कोण POR = 360° – 200° = 160°

अब, ΔPOR में,

OR = OP (वृत्त की त्रिज्याएँ)

∠OPR = ∠ORP (समान भुजाओं के सम्मुख कोण)

पुन: ΔPOR में,

∠OPR + ∠ POR + ∠ORP = 180° (त्रिभुज के अन्त:कोणों को योग 180° होता है।)

∠OPR + 160° + ∠OPR = 180° (∠ORP = ∠OPR)

2 ∠OPR = 180° – 160° = 20°

∠OPR = 10°

अतः ∠OPR = 10°

प्रश्न 4.

∠ABC = 69° और ∠ACB = 31° हो, तो ∠BDC ज्ञात कीजिए।

हल :

दिया है : दी गई आकृति में ∠ABC = 69° और ∠ACB = 31° है।

ज्ञात करना है : ∠BDC का मान।

गणना : ΔABC में,

∠ BAC + ∠ABC + ∠ ACB = 180° (त्रिभुज के अन्त:कोणों का योग 180° होता है।)

∠ BAC + 69° + 31° = 180°

∠BAC = 180° – (69° + 31°) = 180° – 100°

∠BAC = 80°

∠BAC व ∠BDC एक ही वृत्तखण्ड के कोण हैं और ∠ BAC = 80° है।

∠BAC = ∠ BDC = 80°

अत: ∠BDC = 80°

प्रश्न 5.

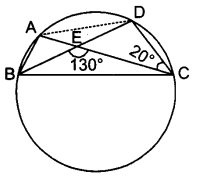
एक वृत्त पर A, B, C और D चार बिन्दु हैं। AC और BD एक बिन्दु E पर इस प्रकार प्रतिच्छेद करते हैं कि ∠ BEC = 130° तथा ∠ECD = 20° है।

∠BAC ज्ञात कीजिए।

हल :

दिया है : दी गई आकृति में एक वृत्त की परिधि पर A, B, C और D चार बिन्दु BF हैं।

AC और BD बिन्दु E पर प्रतिच्छेद करते हैं।

∠BEC = 130° तथा ∠ECD = 20°

ज्ञात करना है: ∠BAC

रचना : AD को मिलाया।

गणना : ∠ ECD = 20° या ∠ACD = 20°

∠ABD वे ∠ACD एक ही वृत्तखण्ड के कोण हैं।

∠ABD = 20° (∠ACD = 20°)

∠ABE = 20°

ΔABE में ∠BEC बहिष्कोण है।

∠ BAE + ∠ ABE = ∠BEC

∠ BAE + 20° = 130° (दिया है ∠BEC = 130°)

∠BAE = 130° – 20° = 110°

∠ BAC = 110° (∠BAE = ∠BAC)

अत: ∠BAC = 110°

प्रश्न 6.

ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिन्दु E पर प्रतिच्छेद करते हैं। यदि ∠DBC = 70° और ∠BAC = 30°हो तो ∠BCDज्ञात कीजिए।

पुनः यदि AB = BC हो तो 2 ECD ज्ञात कीजिए।

हल :

दिया है: ABCD एक चक्रीय चतुर्भुज है जिसमें विकर्ण AC व BD एक-दूसरे को बिन्दु E पर प्रतिच्छेद करते हैं।

∠DBC = 70° व ∠BAC = 30° और AB = BC है।

ज्ञात करना है : ∠ BCD और ∠ECD

गणना : ∠DAC व ∠DBC एक ही वृत्तखण्ड के कोण हैं।

∠ DAC = ∠DBC के ∠DAC = 70° (∠DBC = 70°)

तब, चतुर्भुज ABCD में,

∠DAB = ∠DAC + ∠BAC = 70° + 30°

∠DAB = 100°

ABCD चक्रीय चतुर्भुज है।

∠DAB + ∠BCD = 180° (सम्मुख कोणों का योग 180° होता है।)

100° + ∠ BCD = 180°

∠ BCD = 180° – 100° = 80°

∠BCD = 80°

अब ΔABC में, AB = BC

∠ACB = ∠BAC (समान भुजाओं के सम्मुख कोण)

∠ACB = 30° (∠ BAC = 30°)

ऊपर हम सिद्ध कर चुके हैं कि

∠BCD = 80°

∠ACD + ∠ACB = 80° (चित्र से)

∠ACD + 30° = 80° (∠ACB = 30°)

∠ACD = 80° – 30° = 50°

∠ECD = 50° (∠ ECD = ∠ACD)

अतः ∠BCD = 80° और ∠ECD = 50°

प्रश्न 7.

यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से जाने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि वह एक आयत है।

हल :

दिया है: ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण AC और BD वृत्त के व्यास हैं जो परस्पर बिन्दु O पर काटते हैं।

सिद्ध करना है : ABCD एक आयत है।

उपपत्ति : विकर्ण AC और BD व्यास हैं।

AC = BD

O वृत्त का केन्द्र है।

OA = OC तथा OB = OD

चतुर्भुज ABCD के विकर्ण AC और BD एक-दूसरे को समद्विभाजित करते हैं।

ABCD समान्तर चतुर्भुज है।

∠B = ∠D

परन्तु ABCD चक्रीय चतुर्भुज भी है जिससे

∠B + ∠D = 180° (सम्मुख कोणों का योग = 180°)

उक्त दोनों तथ्यों से ∠B = 90° तथा ∠D = 90°

इसी प्रकार, ∠A = 90° तथा ∠D = 90°

इस प्रकार चतुर्भुज ABCD एक ऐसा समान्तर चतुर्भुज है जिसके अन्त:कोण समकोण हैं।

अत: ABCD एक आयत है।

Proved.

प्रश्न 8.

यदि एक समलम्ब की असमान्तर भुजाएँ बराबर हों तो सिद्ध कीजिए कि वह चक्रीय है।

हल :

दिया है : समलम्ब चतुर्भुज ABCD में भुजा AD = भुजा BC .

सिद्ध करना है : ABCD चक्रीय चतुर्भुज होगा।

रचना : AD के समान्तर रेखाखण्ड BE खींचा।

उपपत्ति : समान्तर चतुर्भुज ABED में,

∠BAD = ∠BED …..(1)

तथा AD = BE

परन्तु

AD = BC (दिया है।)

BC = BE

तब ΔBEC एक समद्विबाहु त्रिभुज हुआ।

∠BEC = ∠ BCE (समान भुजाओं के सम्मुख कोण) …(2)

∠ BEC + ∠ BED = 180° (ऋजु कोण)

∠ BCE + ∠ BAD = 180° [समीकरण (1) व (2) से ]

∠ BCD +∠ BAD = 180°

इससे स्पष्ट है कि चतुर्भुज ABCD के दो सम्मुख अन्त: कोणों का योग दो समकोण के बराबर है।

अत: चतुर्भुज ABCD चक्रीय चतुर्भुज है।

Proved.

प्रश्न 9.

दो वृत्त दो बिन्दुओं B और C पर प्रतिच्छेद करते हैं। B से जाने वाले दो रेखाखण्ड ABD और PBQवृत्तों को A, D और P, Q पर क्रमशः प्रतिच्छेद करते हुए खींचे गए हैं। सिद्ध कीजिए कि ∠ACP = ∠QCD है।

हल :

दिया है : दो वृत्त दी गई आकृति के अनुसार बिन्दुओं B और C पर प्रतिच्छेद करते हैं। दो रेखाखण्ड ABD और PBQ बिन्दु B से जाते हैं। पहला रेखाखण्ड ABD वृत्तों को A व D पर तथा दूसरी PBQ वृत्तों को Pव पर प्रतिच्छेद करता है। C से P और D को मिलाकर ∠ACP और ∠QCD बनाए गए हैं।

सिद्ध करना है :

∠ACP = ∠QCD

उपपत्ति : रेखाखण्ड ABD और PBQ परस्पर बिन्दु B पर काटते हैं।

∠ABP = ∠QBD (शीर्षाभिमुख कोण) …(1)

∠ABP और ∠ACP एक वृत्तखण्ड के कोण हैं।

∠ABP = ∠ACP …(2)

इसी प्रकार, ∠QCD और ∠QBD एक ही वृत्तखण्ड के कोण हैं।

∠QCD = ∠QBD ……(3)

तब समीकरण (1) व (2) से,

∠ACP = ∠QBD …(4)

अब समीकरण (3) व (4) से,

∠ACP = ∠QCD

अतः ∠ACP = ∠QCD

Proved.

प्रश्न 10.

यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएँ, तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित है।

हल :

दिया है : ABC एक त्रिभुज है जिसकी भुजाओं AB तथा AC को व्यास मानकर दो वृत्त खींचे गए हैं जो परस्पर बिन्दु X पर काटते हैं।

सिद्ध करना है : बिन्दु X, त्रिभुज की तीसरी भुजा BC पर स्थित है।

रचना : रेखाखण्ड AX खींचिए।

उपपत्ति : AB वृत्त का व्यास है तथा बिन्दु X वृत्त की परिधि पर स्थित है,

∠AXB = 90° (अर्द्धवृत्त में बना कोण समकोण होता है।)

पुनः AC वृत्त का व्यास है तथा बिन्दु X वृत्त की परिधि पर स्थित है,

∠AXC = 90° (अर्द्धवृत्त में बना कोण समकोण होता है।)

∠AXB + ∠AXC = 90° + 90° = 180°

अर्थात ∠ BXC = 180° = ऋजुकोण

अत: B, X और C एक ही रेखा में स्थित हैं।

वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित है।

Proved.

प्रश्न 11.

उभयनिष्ठ कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC हैं। सिद्ध कीजिए कि ∠ CAD = ∠CBD है।

हल :

दिया है : ΔABC और ΔADC दो समकोण त्रिभुज हैं जिनका कर्ण AC उभयनिष्ठ है। रेखाखण्ड BD खींचा गया है।

सिद्ध करना है : ∠CAD = ∠ CBD

रचना : AC को व्यास मानकर वृत्त खींचा। उपपत्ति

ΔABC समकोण त्रिभुज है जिसका कर्ण AC है।

∠B = 90°

पुनः ΔADC समकोण त्रिभुज है जिसका कर्ण AC है।

∠ D = 90°

तब चतुर्भुज ABCD में, ∠B + ∠D = 180°

ABCD चक्रीय चतुर्भुज है। (सम्मुख कोणों का योग 180° है।)

बिन्दु A, B, C और D एक वृत्त पर हैं।

∠CAD और ∠CBD एक ही वृत्तखण्ड के कोण हैं;

अतः बराबर होंगे।

अतः ∠ CAD = ∠CBD

प्रश्न 12.

सिद्ध कीजिए कि चक्रीय समान्तर चतुर्भुज एक आयत होता है।

हल :

दिया है । समान्तर चतुर्भुज ABCD एक चक्रीय चतुर्भुज है।

सिद्ध करना है : चतुर्भुज ABCD एक आयत है।

उपपत्ति : ABCD एक चक्रीय चतुर्भुज है, इसके सम्मुख कोणों का योग 180° के बराबर होगा।

∠ A + ∠C = 180°

परन्तु समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं।

∠A = ∠C

अत: समीकरण (1) से,

∠A = ∠C = 90° इसी प्रकार,

∠B = ∠D = 90°

ABCD का प्रत्येक अन्त:कोण 90° के बराबर है।

अत: ABCD एक आयत है।

Proved.

प्रश्नावली 10.6 (ऐच्छिक)

प्रश्न 1.

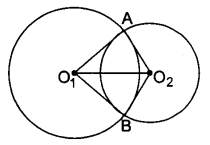
सिद्ध कीजिए कि दो प्रतिच्छेद करते हुए वृत्तों के केन्द्रों की रेखा दोनों प्रतिच्छेद बिन्दुओं पर समान कोण अन्तरित करती है।

हल :

दिया है : O₁ तथा O₂ केन्द्रों वाले दो वृत्त एक-दूसरे को दो बिन्दुओं A तथा B पर प्रतिच्छेद करते हैं।
केन्द्र रेखा O₁O₂ प्रतिच्छेद बिन्दु A पर ∠O₁AO₂ तथा B पर ∠O₁BO₂ अन्तरित करती है।
सिद्ध करना है : ∠O₁AO₂ = ∠O₁BO₂
उपपत्ति: ΔO₁AO₂ तथा ΔO₁BO₂ में,
O₁A = O₁B (एक ही वृत्त की त्रिज्याएँ बराबर होती हैं।)
O₂A = O₂B (एक ही वृत्त की त्रिज्याएँ बराबर होती हैं।)
O₁O₂ = O₁O₂ (दोनों त्रिभुजों की उभयनिष्ठ भुजा है)
ΔO₁AO₂ = ΔO₁BO₂ (S.S.S. से)
∠O₁AO₂ = ∠O₁BO₂ (C.P.C.T.)
Proved.

प्रश्न 2.

एक वृत्त की 5 सेमी तथा 11 सेमी लम्बी दो जीवाएँ AB और CD समान्तर हैं और केन्द्रकी विपरीत दिशा में स्थित हैं। यदि AB और CD के बीच की दूरी 6 सेमी हो, तो वृत्त की त्रिज्या ज्ञात कीजिए।

हल :

दिया है : O त्रिज्या का एक वृत्त है जिसमें AB तथा CD दो समान्तर जीवाएँ केन्द्र O के विपरीत ओर स्थित हैं जिनकी लम्बाइयाँ क्रमश: 5 सेमी व 11 सेमी हैं। जीवाओं के बीच की (लाम्बिक) दूरी 6 सेमी है अर्थात MON = 6 सेमी जबकि MON ⊥ AB व MON ⊥ CD

प्रश्न 3.

किसी वृत्त की दो समान्तर जीवाओं की लम्बाइयाँ 6 सेमी और 8 सेमी हैं। यदि छोटी जीवा केन्द्र से 4 सेमी की दूरी पर हो, तो दूसरी जीवा केन्द्र से कितनी दूर है?

प्रश्न 4.

मान लीजिए कि कोण ABC का शीर्ष एक वृत्त के बाहर स्थित है और कोण की भुजाएँ वृत्त से बराबर जीवाएँ AD और CE काटती हैं। सिद्ध कीजिए कि 2 ABC जीवाओं AC तथा DE द्वारा केन्द्र पर अन्तरित कोणों के अन्तर का आधा है।

प्रश्न 5.

सिद्ध कीजिए कि समचतुर्भुज की किसी भी भुजा को व्यास मानकर खींचा गया वृत्त, उसके विकर्णो के प्रतिच्छेद बिन्दु से होकर जाता है।

हल :

दिया है ABCD एक समचतुर्भुज है जिसमें AC और BD विकर्ण हैं जिनका । प्रतिच्छेद बिन्दु P है।

भुजी BC को व्यास मानकर एक वृत्त खींचा गया है।

सिद्ध करना है: BC को व्यास मानकर खींचा गया वृत्त विकर्मों के प्रतिच्छेद बिन्दु P से होकर जाएगा।

उपपत्ति : ABCD एक समचतुर्भुज है और उसके विकर्ण AC तथा BD परस्पर बिन्दु P पर प्रतिच्छेद करते हैं।

∠CPB = 90°

A CPB एक समकोण त्रिभुज है जिसका कर्ण BC है।

तब समकोण ∆CPB का ∆CPB अर्धवृत्त में स्थित होगा जिसका व्यास BC है।

अत: BC को व्यास मानकर खींचा गया वृत्त बिन्दु P (विकर्मों का प्रतिच्छेद बिन्दु) से होकर जाएगा।

Proved.

प्रश्न 6.

ABCD एक समान्तर चतुर्भुज है। A, B और C से जाने वाला वृत्त CD(यदि आवश्यक हो तो बढ़ाकर) को E पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AE = AD है।

हल :

दिया है : ABCD एक समान्तर चतुर्भुज है जिसके शीर्षों A, B और C से एक वृत्त खींचा गया है जो भुजा CD को E पर काटता है। सिद्ध करना है :

AE = AD

उपपत्ति : ABCD एक समान्तर चतुर्भुज है, ∠B = ∠D …(1) (समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं।)

A, B, C से जाने वाला वृत्त CD को E पर काटता है,

ABCE एक चक्रीय चतुर्भुज है। AED = ∠B …(2)

समीकरण (1) व (2) से,

∠ AED = ∠D (= ∠ADE)

∆ADE में,

∠AED = ∠ADE

∆ADE समद्विबाहु त्रिभुज है जिसमें

AD = AE (समान कोणों की सम्मुख भुजाएँ समान होती हैं।)

अतः AD = AE

Proved.

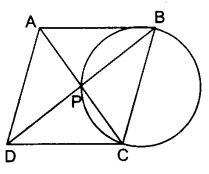
प्रश्न 7.

AC और BD एक वृत्त की जीवाएँ हैं जो परस्पर समद्विभाजित करती हैं। सिद्ध कीजिए :

(i) AC और BD व्यास हैं।

(ii) ABCD एक आयत है।

हल :

दिया है: AC तथा BD एक वृत्त की जीवाएँ हैं जो एक-दूसरे को बिन्दु 0 पर समद्विभाजित करती हैं। सिद्ध करना है :

(i) AC तथा BD वृत्त के व्यास हैं।

(ii) ABCD एक आयत है।

रचना : चतुर्भुज ABCD को पूरा किया।

उपपत्ति : (i) जीवा AC और BD एक-दूसरे को बिन्दु O पर समद्विभाजित करती हैं।

OA = OB = OC = OD

तब, OA, OB, OC और OD एक ऐसे वृत्त की त्रिज्याएँ हैं जिसका केन्द्र O है।

तब, AC = OA + OC = त्रिज्या + त्रिज्या = 2 x त्रिज्या

AC वृत्त का व्यास है।

BD भी O से होकर जाती है, तब BD भी वृत्त का व्यास है।

Proved.

(ii) AC व्यास है, तब ∠B = 90° तथा ∠D = 90° और BD व्यास है,

तब ∠A = 90° तथा ∠C = 90° (अर्द्धवृत्त में बना कोण समकोण होता है।)

तब, ABCD एक ऐसा चतुर्भुज है जिसका प्रत्येक अन्त: कोण 90° है तथा विकर्ण एक-दूसरे को अर्धित करते हैं।

अत: ABCD एक आयत है।

Proved.

प्रश्न 8.

त्रिभुज ABC के कोणों A, B और C के समद्विभाजक उसके परिवृत्त को क्रमशः बिन्दुओं D, E और F पर प्रतिच्छेदित करते हैं। | सिद्ध कीजिए कि ∆DEF के कोण  90° – , 90° – और 90° – हैं।

प्रश्न 9.

दो सर्वांगसम वृत्त परस्पर बिन्दुओं A और B पर प्रतिच्छेद करते हैं। A से होकर कोई रेखाखण्ड PAQइस प्रकार खींचा गया है कि P और २ दोनों वृत्तों पर स्थित हैं। सिद्ध कीजिए कि BP = BQ है।

हल :

दिया है : दो वृत्तों के केन्द्र O₁ व O₂ हैं और वे बिन्दुओं A और B पर प्रतिच्छेद करते हैं। A से एक रेखा PAQ खींची गई है जो वृत्तों से बिन्दुओं P और Q पर मिलती है।
सिद्ध करना है : रेखाखण्ड BP = रेखाखण्ड BQ
रचना : जीवा AB तथा त्रिज्याएँ O₁A, O₁B, O₁A तथा O₂B खींचीं
उपपत्ति : जीवा AB दोनों वृत्तों में उभयनिष्ठ है और दोनों वृत्त सर्वांगसम हैं।
O1 केन्द्र वाले वृत्त का चाप AB = O₂ केन्द्र वाले वृत्त का चाप AB
∠AO₁B = ∠AOB (सर्वांगसम वृत्तों के समान चाप केन्द्र पर समान कोण अन्तरित करते हैं।)
∠APB = ∠AQB (परिधि पर अन्तरित कोण)
अब : ΔQBP में,
∠APB = ∠AQB (ऊपर सिद्ध हुआ है।)
∠BPQ = ∠BQP
अत: BQ = BP (सम्मुख कोण बराबर होने पर सम्मुख भुजाएँ भी बराबर होती हैं।)
Proved.

प्रश्न 10.

किसी त्रिभुज ABC में, यदि ∠A का समद्विभाजक तथा BC का लम्बे समद्विभाजक प्रतिच्छेद करें, तो सिद्धकीजिए कि वे ΔABC के परिवृत्त पर प्रतिच्छेद करेंगे।

हल :

दिया है : ΔABC के आधार BC का लम्ब समद्विभाजक XY है।

ABDC, ΔABC का परिवृत्त है। लम्ब समद्विभाजक XY परिवृत्त को D पर काटता है। XY, BC को M पर काटता है।।

सिद्ध करना है : ∠A का समद्विभाजक भी बिन्दु D से होकर जाएगा।

रचना : DB तथा DC को मिलाया।

उपपत्ति : XY, BC का लम्ब समद्विभाजक है और यह परिवृत्त को बिन्दु D पर काटता है।

बिन्दु D, परिवृत्त पर भी है और XY पर भी।

ΔBDM और ΔCDM में,

BM = CM (XY, BC का लम्ब समद्विभाजक है।)

∠BMD = ∠CMD (XY ⊥ BC अर्थात प्रत्येक 90°)

MD = MD (उभयनिष्ठ भुजा है।)

ΔBDM = ΔCDM (S.A.S. से)

BD = CD (C.P.C.T.)

बिन्दु D, परिवृत्त पर भी स्थित है।

परिवृत्त में, जीवा BD = जीवा CD

चाप BD= चाप CD (समान चाप किसी वृत्त की समान जीवाएँ काटती हैं।)

चाप BD द्वारा बिन्दु A पर अन्तरित कोण = चाप CD द्वारा बिन्दु A पर अन्तरित कोण

∠BAD = ∠CAD

अत: A का समद्विभाजक AD भी बिन्दु D से होकर जाता है।

Proved.

एनसीईआरटी सोलूशन्स क्लास 9 गणित पीडीएफ

• 1. संख्या पद्धति
• 2. बहुपद
• 3. निर्देशांक ज्यामिति
• 4. दो चरों वाले रैखिक समीकरण
• 5. यूक्लिड की ज्यामिति का परिचय
• 6. रेखाएँ और कोण
• 7. त्रिभुज
• 8. चतुर्भुज
• 9. समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
• 11. रचनाएँ
• 12. हीरोन का सूत्र
• 13. पृष्ठीय क्षेत्रफल और आयतन
• 14. सांख्यिकी
• 15. प्रायिकता