NCERT Solutions Class 9 गणित Chapter-11 (रचनाएँ)
Class 9 गणित
पाठ-11 (रचनाएँ)
अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर
प्रश्नावली 11.1
प्रश्न 1.
एक दी हुई किरण के प्रारम्भिक बिन्दु पर 90° के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए।
हल:
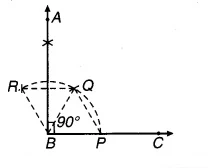
चित्र 11.9
रचना :
(i) किरण BC के प्रारम्भिक बिन्दु B को केन्द्र मानकर किसी त्रिज्या से एक चाप खींचिए जो BC को बिन्दु P पर प्रतिच्छेद करता है।
(ii) P को केन्द्र लेकर इसी त्रिज्या से चाप PQ काटिए।
(iii) Q को केन्द्र लेकर इसी त्रिज्या से पुनः चाप QR काटिए।
(iv) Q और R को क्रमशः केन्द्र लेकर QR के आधे से अधिक की त्रिज्या लेकर चाप खींचिए जो परस्पर A बिन्दु पर प्रतिच्छेद करते हैं।
(v) किरण BA खींचिए।
यही ∠ABC = 90° का अभीष्ट कोण है।
कारण : PQ, QR, BQ एवं BR को मिलाइए।
चूँकि BP = PQ = BQ ⇒ ∆QBP एक समबाहु त्रिभुज है। (रचना से)
⇒ OBP = 60° (समबाहु ∆ का कोण है) ….(1)
चूँकि QB = QR = BR = ∆ BQR एक समबाहु त्रिभुज है (रचना से)
⇒ ∠QBR = 60° (समबाहु ∆ का कोण है) …(2)
चूँकि किरण AB, ∠QBR का अर्द्धक है (रचना से)
⇒ ∠QBA = = x 60° = 30° ….(3)
⇒ ∠QBP + ∠QBA = 60° + 30° = 90°
समीकरण (1) + (3) से]
अतः ABC = 90°. (चित्रानुसार) इति सिद्धम्
प्रश्न 2.
एक दी हुई किरण के प्रारम्भिक बिन्दु पर 45° के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए।
हल:
रचना :
(i) किरण BC के प्रारम्भिक बिन्दु B को केन्द्र लेकर किसी त्रिज्या से एक चाप खींचिए जो BC को बिन्दु P पर प्रतिच्छेद करता है।
(ii) Pको केन्द्र लेकर उसी त्रिज्या से एक चाप खींचिए जो पूर्व चाप को बिन्दु Q पर प्रतिच्छेद करता है।
(iii) कोण ∠PBQ की समद्विभाजक किरण BR खींचिए जो पूर्व चाप को बिन्दु S पर प्रतिच्छेद करती है।
(iv) कोण ∠ SBQ की समद्विभाजक किरण BA खींचिए।
चित्र 11.10
यही ∠ABC = 45° का अभीष्ट कोण है।
कारण : PQ एवं BQ को मिलाइए।
चूँकि BP = PQ = BQ ⇒ ∆QBP एक समबाहु त्रिभुज है। (रचना से)
⇒ ∠QBP = 60° (समबाहु A का कोण है)
चूँकि किरण BR, ∠QBP की समद्विभाजक है। (रचना से)
⇒ ∠QBR = ∠ RBC =
चूँकि किरण BA, ∠QBR की समद्विभाजक है। (रचना से)
⇒ ∠ABR =
∠ABR + ∠RBC = 15° + 30° = 45° . [समी (1) + (2) से]
अतः ∠ABC = 45°. (चित्रानुसार)
इति सिद्धम
प्रश्न 3.
निम्न मापों के कोणों की रचना कीजिए :
(i) 30° (2018)
(ii) 22
(iii) 15°.
हल:
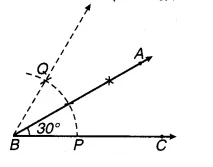
चित्र 11.11
(i) रचना : (a) किरण BC खींचिए।
(b) किरण BC के प्रारम्भिक बिन्दु B को केन्द्र लेकर किसी त्रिज्या से एक चाप खींचिए जो किरण BC को बिन्द P A पर प्रतिच्छेद करता है।
(c) P को केन्द्र लेकर उसी त्रिज्या से एक चाप खींचिए जो पहले चाप को बिन्दु O पर प्रतिच्छेद करता है।
(d) कोण QBP की समद्विभाजक किरण BA खींचिए। यही ∠ABC = 30° का अभीष्ट कोण है।
(ii) रचना :
चित्र 11.12
(a) किरण BC खींचिए।
(b) B को केन्द्र लेकर किसी त्रिज्या से एक चाप खींचिए A जो BC को P पर प्रतिच्छेद करता है।
(c) P को केन्द्र लेकर उसी त्रिज्या से एक चाप खींचिए का जो पहले चाप को Q पर प्रतिच्छेद करता है।
(d) ∠OBP की समद्विभाजक किरण BR खींचिए।
(e) ∠RBC की समद्विभाजक किरण BS खींचिए।
(f) ∠ RBS की समद्विभाजक किरण BA खींचिए।
यही ∠ ABC = 22
(iii) रचना :
चित्र 11.13
(a) किरण BC खींचिए।
(b) B को केन्द्र लेकर किसी त्रिज्या से एक चाप खींचिए जो किरण BC को P पर प्रतिच्छेद करती है।
(c) P को केन्द्र लेकर उसी त्रिज्या से एक चाप खींचिए जो पहले चाप को बिन्दु Q पर प्रतिच्छेद करता है।
(d) ∠QBP की समद्विभाजक किरण BR खींचिए।
(e) ∠RBC की समद्विभाजक किरण BA खींचिए। यही ∠ABC = 15° का अभीष्ट कोण है।
प्रश्न 4.
निम्न कोणों की रचना कीजिए और चाँदे द्वारा मापकर पुष्टि कीजिए :
(i) 75° (2019)
(ii) 1050
(iii) 135°.
हल:
(i) रचना :
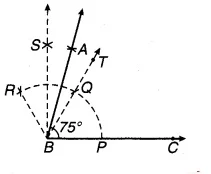
चित्र 11.14
(a) किरण BC खींचिए।
(b) बिन्दु B को केन्द्र लेकर किसी त्रिज्या से एक चाप खींचिए जो BC को बिन्दु P पर प्रतिच्छेद करता है।
(c) P को केन्द्र लेकर उसी त्रिज्या से चाप PQ तथा Q को केन्द्र लेकर उसी त्रिज्या से चाप QR काटिए।
(d) ∠ RBO की समद्विभाजक किरण BS खींचिए।
(e) ∠ SBQ की समद्विभाजक किरण BA खींचिए।
यही ∠ ABC = 75° का अभीष्ट कोण है जिसकी पुष्टि चाँदे से नापने पर होती है।
(ii) रचना :
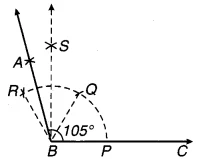
चित्र 11.15
(a) किरण BC खींचिए।
(b) B को केन्द्र लेकर किसी त्रिज्या से एक चाप खींचिए जो किरण BC को बिन्दु P पर प्रतिच्छेद करता है।
(c) P को केन्द्र लेकर उसी त्रिज्या से PQ चाप एवं ए को केन्द्र लेकर उसी त्रिज्या से QR चाप खींचिए।
(d) ∠QBR का समद्विभाजक BS खींचिए।
(e) ∠ SBR का समद्विभाजक BA खींचिए।
यही ∠ABC = 105° का अभीष्ट कोण है जिसकी पुष्टि चाँदे से नापने पर होती है।
(iii) रचना :
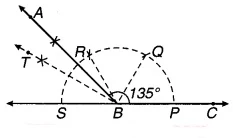
चित्र 11.16
(a) किरण BC खींचिए।
(b) B को केन्द्र लेकर किसी त्रिज्या से एक चाप खींचिए जो किरण BC को बिन्दु P पर प्रतिच्छेद करती है।
(c) P को केन्द्र लेकर उसी त्रिज्या से PQ, Q को केन्द्र लेकर QR एवं R को केन्द्र लेकर RS चाप खींचिए।
(d) ∠ RBS का समद्विभाजक BT खींचिए।
(e) ∠RBT का समद्विभाजक BA खींचिए।
यही ∠ABC = 135° का अभीष्ट कोण है जिसकी पुष्टि चाँदे से नापने पर होती है।
प्रश्न 5.
एक समबाहु ∆ की रचना कीजिए जब इसकी भुजा दी हो तथा कारण सहित रचना की पुष्टि कीजिए।
हल:
रचना :
चित्र 11.17
(i) दी हुई भुजा की लम्बाई के बराबर लम्बाई का एक रेखाखण्ड BC खींचिए।
(ii) B और C को केन्द्र लेकर BC के बराबर त्रिज्या से क्रमश: चाप खींचिए जो परस्पर A बिन्दु पर प्रतिच्छेद करते हैं।
(iii) AB और AC को मिलाइए। यही ∆ABC अभीष्ट समबाहु त्रिभुज है जिसकी भुजा दी हुई है।
कारण : AB = BC = AC (रचना से)
अत: ∆ABC समबाहु ∆ है।
प्रश्न 1.
एक त्रिभुज ABC की रचना कीजिए जिसमें BC = 7 cm, ∠B = 75° और AB + AC = 13 cm है। (2018, 19)
हल:
रचना :
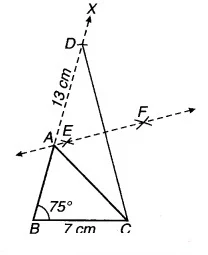
चित्र 11.18
(i) BC = 7 cm का रेखाखण्ड खींचिए।
(ii) रेखाखण्ड BC के बिन्दु B पर ∠DBC = 75° का कोण बनाते हुए एक किरण BX खींचिए।
(iii) किरण BX में से BD = 13 cm का रेखाखण्ड लीजिए।
(iv) DC को मिलाइए।
(v) DC का लम्ब समद्विभाजक EF खींचिए।
(vi) जो BD को बिन्दु A पर प्रतिच्छेद करता है।
(vii) AC को मिलाइए।
यही ∆ABC अभीष्ट त्रिभुज है।
प्रश्न 2.
एक त्रिभुज ABC की रचना कीजिए जिसमें BC = 8 cm, ∠B = 45° और AB – AC = 3.5 cm है।
हल:
रचना :
चित्र 11.19
(i) BC = 8 cm का एक रेखाखण्ड खींचिए।
(ii) BC के साथ बिन्दु B पर ∠DBC = 45° का कोण बनाते हुए किरण BX खींचिए।
(iii) किरण BX में से BD = 3.5 cm का रेखाखण्ड लीजिए।
(iv) DC को मिलाइए।
(v) DC का लम्ब समद्विभाजक EF खींचिए जो Bx को B बिन्दु A पर प्रतिच्छेद करता है।
(vi) AC को मिलाइए।
यही ∆ABC अभीष्ट त्रिभुज है।
प्रश्न 3.
एक त्रिभुज PQR की रचना कीजिए जिसमें OR = 6 cm, ∠Q= 60° और PR – PQ = 2 cm हो।
हल:
रचना :
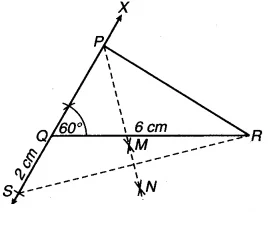
चित्र 11.20
(i) एक रेखाखण्ड QR = 6 cm खींचिए।
(ii) रेखाखण्ड QR के साथ 60° का कोण बनाते हुए किरण Qx खींचिए।
(iii) QS = 2 cm का एक रेखाखण्ड किरण Qx में से काटिए।
(iv) SR को मिलाइए।
(v) SR का लम्ब समद्विभाजक AB खींचिए जो Qx को बिन्दु P पर प्रतिच्छेद करता है।
(vi) PR को मिलाइए। यही ∠∆POR अभीष्ट त्रिभुज है।
प्रश्न 4.
एक त्रिभुज XYZ की रचना कीजिए जिसमें ∠Y = 30°, ∠Z = 90° और XY+ YZ + ZX = 11 cm हो।
हल:
रचना:
चित्र 11.21
(i) एक रेखाखण्ड PO = 11 cm खींचिए।
(ii) बिन्दु P पर 30° एवं बिन्दु O पर 90° का कोण बनाते हुए किरण PR एवं Qs खींचिए।
(iii) ∠RPO एवं ∠SOP के समद्विभाजक खींचिए जो परस्पर बिन्दु X पर प्रतिच्छेद करते हैं।
(iv) PX एवं QX के लम्ब समद्विभाजक खींचिए जो PQ को क्रमशः Y और Z बिन्दुओं पर प्रतिच्छेद करते हैं।
(v) XY एवं XZ को मिलाइए। यही ∆XYZ अभीष्ट त्रिभुज है।
प्रश्न 5.
एक समकोण त्रिभुज की रचना कीजिए जिसका आधार 12 cm और कर्ण तथा अन्य भुजा का योग 18 cm है।
हल:
एक समकोण ∆ABC की रचना करनी है जिसका ∠B समकोण है, आधार BC = 12 cm है तथा कर्ण AC + भुजा AB = 18 cm.
रचना:
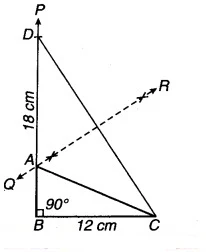
चित्र 11.22
(i) BC = 12 cm का एक रेखाखण्ड खींचिए।
(ii) BC के बिन्दु B पर BC के साथ समकोण (90° का कोण) बनाते हुए एक किरण BP खींचिए।
(iii) किरण BP में से BD = 18 cm का एक रेखाखण्ड काटिए।
(iv) DC को मिलाइए।
(v) DC का लम्ब समद्विभाजक OR खींचिए जो BD को बिन्दु A पर प्रतिच्छेद करता है।
(vi) AC को मिलाइए।
यह ∆ABC अभीष्ट समकोण त्रिभुज है।