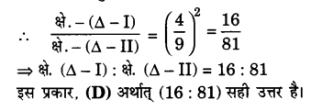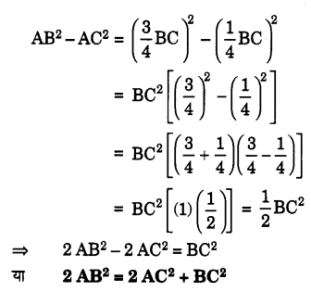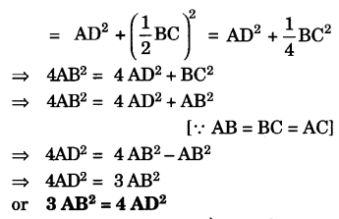NCERT Solutions Class 10 गणित Chapter-6 (त्रिभुज)

NCERT Solutions Class 10 गणित 10 वीं कक्षा से Chapter-6 (त्रिभुज) के उत्तर मिलेंगे। यह अध्याय आपको मूल बातें सीखने में मदद करेगा और आपको इस अध्याय से अपनी परीक्षा में कम से कम एक प्रश्न की उम्मीद करनी चाहिए।

हमने NCERT बोर्ड की टेक्सटबुक्स हिंदी गणित के सभी Questions के जवाब बड़ी ही आसान भाषा में दिए हैं जिनको समझना और याद करना Students के लिए बहुत आसान रहेगा जिस से आप अपनी परीक्षा में अच्छे नंबर से पास हो सके।

एनसीईआरटी प्रश्न-उत्तर

Class 10 गणित

पाठ-6 (त्रिभुज)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्नावली 6.1

प्र. 1. कोष्ठकों में दिए शब्दों में से सही शब्दों का प्रयोग करते हुए, रिक्त स्थानों को भरिए :

(i) सभी वृत्त …….. होते है| (सर्वांगसम, समरूप)

(ii) सभी वर्ग…… होते हैं| (समरूप, सर्वांगसम)

(iii) सभी …….. त्रिभुज समरूप होते है | (समद्विबाहु, समबाहु)

(iv) भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि

(i) उनके संगत कोण ……..हो तथा

(ii) उनकी संगत ……भुजाएँ हों| (बराबर, समानुपाती|

हलः

(i) सभी वृत्त समरूप होते हैं।

(ii) सभी वर्ग समरूप होते हैं।

(iii) सभी समबाहु त्रिभुज समरूप होते हैं।

(iv) भुजाओं की समान संख्या वाले दो बहुभुजे समरूप होते हैं, यदि

(i) उनके संगत कोण बराबर हों तथा

(ii) उनकी संगत समानुपाती भुजाएँ हों।

प्र० 2. निम्नलिखित युग्मों के दो भिन्न-भिन्न उदाहरण दीजिएः

(i) समरूप आकृतियाँ

(ii) ऐसी आकृतियाँ जो समरूप नहीं हैं।

हलः

(i) (a) दो वृत्त परस्पर समरूप होते हैं।

(b) दो वर्ग परस्पर समरूप होते हैं।

(ii) (a) एक वृत्त और एक त्रिभुज समरूप नहीं होते हैं।

(b) एक समद्विबाहु त्रिभुज और एक विषमबाहु। त्रिभुज समरूप आकृतियाँ नहीं होती हैं।

प्र० 3. बताइए कि निम्न चतुर्भुज समरूप हैं या नहीं:

हलः

संगत भुजाएँ समानुपाती हैं, परन्तु इनके संगत कोण समान नहीं हैं। ये आकृतियाँ समरूप नहीं हैं।

प्रश्नावली 6.2

प्र० 1. आकृति (i) और (ii) में, DE || BC और (i) में EC और (ii) में AD ज्ञात कीजिए :

प्र० 2. किसी त्रिभुज PQR की भुजाओं PQ और PR पर क्रमशः बिन्दु E और F स्थित हैं| निम्नलिखित में से प्रत्येक स्थिति के लिए, बताइए कि क्या EF || QR है|

(i) PE = 3.9 cm, EQ = 3cm, PF = 3.6 और FR = 2.4 cm

(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm और RF = 9 cm

(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm और PF = 0.36 cm

प्र० 3. आकृति में यदि LM || CB और LN || CD हो तो सिद्ध कीजिए कि $\frac { AM }{ AB }$ = $\frac { AN }{ AD }$ है।

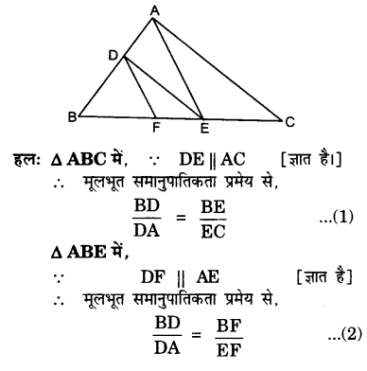
प्र० 4. आकृति में DE || AC और DF || AE है। सिद्ध कीजिए कि $\frac { BF }{ FE }$ = $\frac { BE }{ EC }$ है।

प्र० 5. आकृति में DE || OQ और DF || OR है। दर्शाइए कि EF || QR है।

प्र० 6. आकृति में क्रमशः OP, OQ और OR पर स्थित बिंदु A, B और C इस प्रकार हैं कि AB || PQ और AC || PR है। दर्शाइए कि BC || QR है।

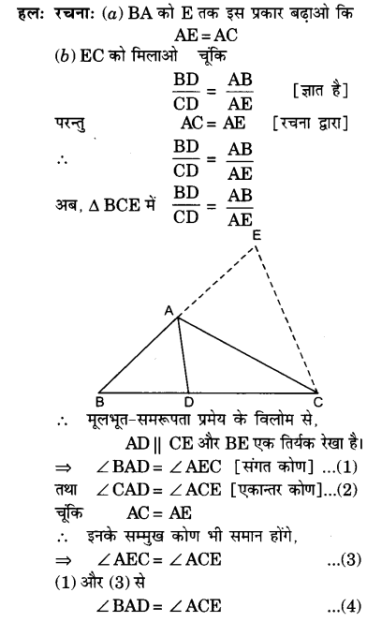
प्र० 7. थेल्स प्रमेय का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है। ( याद कीजिए कि आप इसे कक्षा IX में सिद्ध कर चुके हैं।)

हलः हमें ज्ञात है कि एक ΔABC में भुजा AB का मध्य बिन्दु D तथा AC पर E इस प्रकार है कि

प्र० 8. थेल्स प्रमेय का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाली रेखा तीसरी भुजा के समांतर होती है। (याद कीजिए कि आप कक्षा IX में ऐसा कर चुके हैं)।

प्र० 9. ABCD एक समलंब है जिसमें AB || DC है तथा इसके विकर्ण परस्पर बिंदु O पर प्रतिच्छेद करते हैं। दर्शाइए कि $\frac { AO }{ BO }$ = $\frac { CO }{ DO }$ हैं।

प्र० 10. एक चतुर्भुज ABCD के विकर्ण परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि $\frac { AO }{ BO }$ = $\frac { CO }{ DO }$ है। दर्शाइए कि ABCD एक समलंब है।

प्रश्नावली 6.3

प्र० 1. बताइए कि आकृति 6.34 में दिए त्रिभुजों के युग्मों में से कौन – कौन से युग्म समरूप हैं | उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देनें में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए|

प्र० 2. आकृति में, ΔODC ~ ΔOBA, ∠BOC = 125° और ∠CDO = 70° है| ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए|

प्र० 3. समलंब ABCD, जिसमे AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं| दो त्रिभुजों की समरूपता कसौटी का प्रयोग करते हुए, दर्शाइए दर्शाइए कि $\frac { OA }{ OC }$ = $\frac { OB }{ OD }$ है|

प्र० 4. आकृति में, $\frac { QR }{ QS }$ = $\frac { QT }{ PR }$ तथा ∠1 = ∠2 है। दर्शाइए कि ΔPQS ~ ΔTQR है।

प्र० 5. ΔPQR की भुजाओं PR और QR पर क्रमश: बिंदु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है| दर्शाइए कि ΔRPQ ~ ΔRTS है|

प्र० 6. आकृति में, यदि ΔABE ≅ ΔACD है, तो दर्शाइए कि ΔADE ~ ΔABC है|

प्र० 7. आकृति में, ΔABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं तो दर्शाइए कि :

(i) ΔAEP ~ ΔCDP

(ii) ΔABD ~ ΔCBE

(iii) ΔAEP ~ ΔADB

(iv) ΔPDC ~ ΔBEC

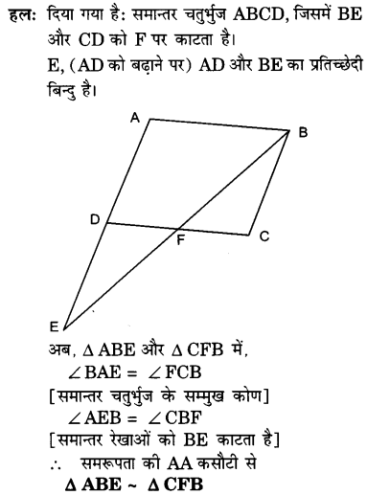
प्र० 8. समान्तर चतुर्भुज ABCD की बढाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है| दर्शाइए कि ΔABE ~ ΔCFB है |

प्र० 9. आकृति में, ABC और AMP दो समकोण त्रिभुज है, जिसके कोण B और M समकोण हैं| सिद्ध कीजिए कि :

(i) ΔABC ~ ΔAMP

(ii) $\frac { CA }{ PA }$ = $\frac { BC }{ MP }$

हलः हमें दिया गया है:

समकोण ΔABC जो कि B पर समकोण है।

तथा ΔAMP जिसमें M पर समकोण है।

∠B = ∠M = 90° ……(1)

(i) ΔABC और ΔAMP में,

∠ABC = ∠AMP [(1) से]

और ∠BAC = ∠MAP [उभयनिष्ठ]

समरूपता की AA कसौटी से,

ΔABC ~ ΔAMP

(ii) ΔABC ~ ΔAMP [ऊपर सिद्ध किया गया है]

इनकी संगत भुजाएँ समानुपाती हैं।

$\frac { CA }{ PA }$ = $\frac { BC }{ MP }$

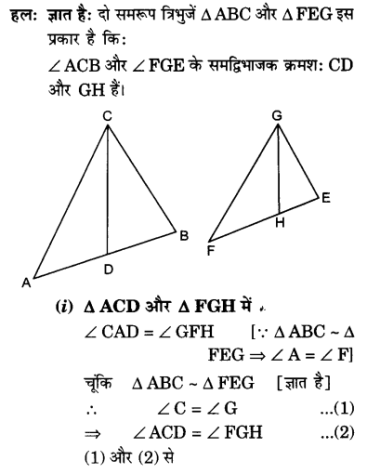
प्र० 10. CD और GH क्रमश: ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिंदु D और H क्रमश: ΔABC और ΔFEG की भुजाओं AB और FE पर स्थित हैं| यदि ΔABC ~ ΔFEG है, तो दर्शाइए कि :

(i) $\frac { CD }{ GH }$ = $\frac { AC }{ FG }$

(ii) ΔDCB ~ ΔHGE

(iii) ΔDCA ~ ΔHGF

प्र० 11. आकृति में, AB = AC वाले, एक समद्विबाहु त्रिभुज ABC की बढाई गई भुजा CB पर स्थित E एक बिन्दु है| यदि AD ⊥ BC और EF ⊥ AC है तो सिद्ध कीजिए कि ΔABD ~ ΔECF है|

हलः हमें प्राप्त है।

एक समद्विबाहु ΔABC जिसमें AB = AC

अब, ΔABD और ΔECF में,

चूंकि AB = AC [ज्ञात है]

और समान भुजाओं के सम्मुख कोण समान होते हैं।

∠ACB = ∠ABC

∠ECF = ∠ABD …(1)

पुनः AD ⊥ BC और EF ⊥ AC

∠ADB = ∠EFC = 90° …(2)

(1) और (2) से ΔABD ~ ΔECF [AA समरूपता से]

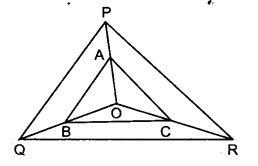
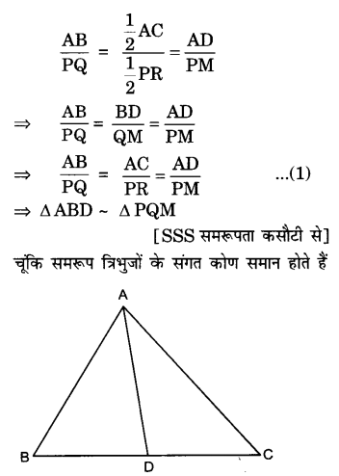
प्र० 12. एक त्रिभुज ABC कि भुजाएँ AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा माध्यिका PM के समानुपाती हैं (देखिए आकृति)| दर्शाइए कि ΔABC ~ ΔPQR है|

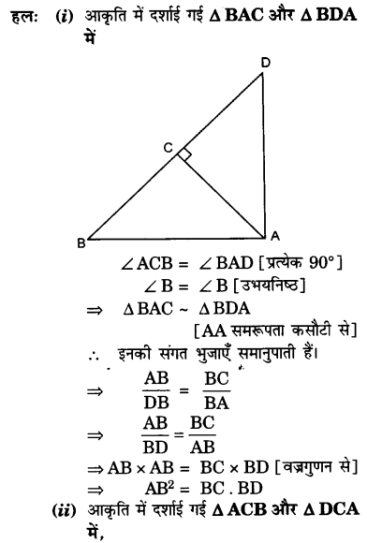
प्र० 13. एक त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि ∠ADC = ∠BAC है| दर्शाइए कि CA² = CB.CD है|

हलः ज्ञात है: ΔABC जिसकी भुजा BC पर एक बिन्दु D

इस प्रकार है कि ∠ADC = ∠BAC

अब, ΔABC और ΔADC में,

∠BAC = ∠ADC [ज्ञात है]

और ∠BCA = ∠DCA [उभयनिष्ठ]

AA समरूपता कसौटी द्वारा,

ΔBAC ~ ΔADC

इनकी संगत भुजाएँ समानुपाती हैं।
$\frac { CA }{ CD }$ = $\frac { CB }{ CA }$

CA x CA = CB x CD

CA² = CB x CD

प्र० 14. एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं| दर्शाइए कि ΔABC ~ ΔPQR है|

प्र० 15. लंबाई 6m वाले एक उध्वार्धर स्तम्भ की भूमि पर छाया की लंबाई 4m है, जबकि उसी समय एक मीनार की छाया की लंबाई 28 m है| मीनार की ऊँचाई ज्ञात कीजिए|

प्र० 16. AD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं, जबकि ΔABC ~ ΔPQR है। सिद्ध कीजिए कि $\frac { AB }{ PQ }$ = $\frac { AD }{ PM }$ है|

प्रश्नावली 6.4

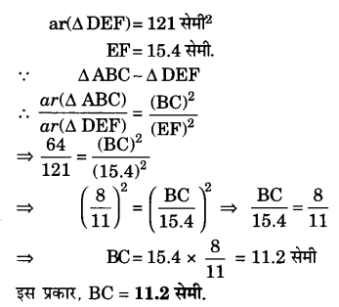
प्र० 1. मान लीजिए ΔABC ~ ΔDEF और इनके क्षेत्रफल क्रमशः 64 cm2 और 121 cm2 हैं| यदि EF = 15.4 cm² हो, तो BC ज्ञात कीजिए |

हलः हमें प्राप्त है।

ar(ΔABC) = 64 cm2

प्र० 2. एक समलंब ABCD जिसमें AB || DC हैं, के विकर्ण परस्पर बिन्दु O पर प्रतिच्छेद करते हैं| यदि AB = 2 CD हो तो ΔAOB और ΔCOD के क्षेत्रफलों का अनुपात ज्ञात कीजिए|

हलः हमें प्राप्त है: समलंब ABCD में, AB | DC

विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं।

ΔAOB और ΔCOD में,

∠AOB = ∠COD [शीर्षभिमुख कोण]

∠OAB = ∠OCD [एकान्तर कोण]

प्र० 3. आकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए हैं| यदि AD, BC कोप O पर प्रतिच्छेद करे, तो दर्शाइए की

प्र० 4.यदि दो समरूप तत्रिभुजों के क्षेत्रफल बराबर हों तो सिद्ध कीजिए कि वे त्रिभुज सर्वान्गसम होते हैं|

प्र० 5. एक त्रिभुज ABC की भुजाओं AB, BC और CA के मध्य-बिन्दु क्रमशः D, E और F हैं| त्रिभुज DEF और त्रिभुज ABC के क्षेत्रफलों का अनुपात ज्ञात कीजिए|

हलः हमें प्राप्त है: ΔABC में भुजाओं AB, AC और BC

के मध्य बिन्दु क्रमशः D, E और F हैं।

D, F और F को मिलाने पर ΔDEF बनता है

अब, D भुजा AB का मध्य बिंदु है।

प्र० 6. सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत माध्यिकाओं के अनुपात का वर्ग होता है|

हलः हमें प्राप्त है: ΔABC और ΔDEF इस प्रकार है कि ΔABC ~ ΔDEF

तथा AM और DN क्रमशः भुजाओं BC और EF’ के संगत माध्यिकाएँ हैं।

चूंकि ΔABC ~ ΔDEF

इनके क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के वर्गों के अनुपात के समान होगी।

प्र० 7. सिद्ध कीजिए कि दो एक वर्ग की किसी भुजा पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल उसी वर्ग के एक विकर्ण पर बनाए गए समबाहु त्रिभुज के क्षेत्रफल का आधा होता है |

हलः हमें प्राप्त है कि वर्ग ABCD में विकर्ण AC है।

भुजा BC पर समबाहु ΔBQC और विकर्ण AC पर समबाहु ΔAPC बनाई गई है।

सभी समबाहु त्रिभुजें समरूप होती हैं।

प्र० 8. ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कोई भुजद BC का मध्य-बिन्दु है| त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात है:

(A) 2 : 1

(B) 1 : 2

(C) 4 : 1

(D) 1 : 4

हलः हमें प्राप्त है।

समबाहु ΔABC में, भुजा BC का मध्यबिंदु D है। DE को इस प्रकार खींचा गया है कि ΔBDE भी एक समबाहु त्रिभुज है।

चूंकि सभी समबाहु त्रिभुजें समरूप होती हैं।

ΔABC ~ ΔBDE

इनके क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के वर्गों के अनुपात के समान होता है।

प्र० 9. दो समरूप त्रिभुजों की भुजाएँ 4 : 9 के अनुपात में हैं| इन त्रिभुजों के क्षेत्रफलों का अनुपात है :

(A) 2 : 3

(B) 4 : 9

(C) 81 : 16

(D) 16 : 81

हलः हमें दो समरूप त्रिभुजें इस प्रकार प्राप्त हैं कि उनकी संगत भुजाओं का अनुपात 4:9 है।

चूंकि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के समान होता है।

प्रश्नावली 6.5

प्र० 1. कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धरित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।

(i) 7 cm, 24 cm, 25 cm

(ii) 3 cm, 8 cm, 6 cm

(iii) 50 cm, 80 cm, 100 cm

(iv) 13 cm, 12 cm, 5 cm

प्र० 2. PQR एक समकोण त्रिभुज है जिसका कोण P समकोण है तथा QR पर बिंदु M इस प्रकार स्थित है कि PM ⊥ QR है | दर्शाइए कि PM² = QM . MR है|

प्र० 3. आकृति 6.53 में ABD एक समकोण त्रिभुज है| जिसका कोण A समकोण है तथा AC ⊥ BD है| दर्शाइए कि

(i) AB² = BC . BD

(ii) AC² = BC . DC

(iii) AD² = BD . CD

प्र० 4. ABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है| सिद्ध कीजिए कि AB² = 2AC² है|

प्र० 5. ABC एक समद्विबाहु त्रिभुज है जिसमें AC = BC है| यदि AB² = 2AC² है, तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है|

प्र० 6. एक समबाहु त्रिभुज ABC की भुजा 2a है। उसके प्रत्येक शीर्षलंब की लंबाई ज्ञात कीजिए।

प्र० 7. सिद्ध कीजिए कि एक समचतुर्भुज की भुजाओं के वर्गों का योग उसके विकर्णों के वर्गों के योग के बराबर होता है।

प्र० 9. 10 मी. लंबी एक सीढ़ी एक दीवार पर टिकाने पर भूमि से 8 मी. की ऊँचाई पर स्थित एक खिड़की तक पहुंचती है। दीवार के आधार से सीढ़ी के निचले सिरे की दूरी ज्ञात कीजिए।

प्र० 10. 18 मी. ऊंचे एक ऊर्ध्वाधर खंभे के ऊपरी सिरे से एक तार का एक सिरा जुड़ा हुआ है तथा तार का दूसरा सिरा एक बूंटे से जुड़ा हुआ है। खंभे के आधार से बँटे को कितनी दूरी पर गाड़ा जाए कि तार तना रहे जबकि तार की लंबाई 24 मी. है।

हलः माना AB एक तार तथा BC एक खंभा है।

माना बिन्दु A एक बँटे को प्रकट करता है।

AB = 24 मी. और BC = 18 मी.

अब, समकोण ΔABC में पाईथागोरस प्रमेय द्वारा।

प्र० 11. एक हवाई जहाज एक हवाई अड्डे से उत्तर की ओर 1000 कि.मी./घं. की चाल से उड़ता है। इसी समय एक अन्य हवाई जहाज उसी हवाई अड्डे से पश्चिम की ओर 1200 कि.मी./घं. की चाल से उड़ता है। 1 $\frac { 1 }{ 2 }$ घंटे के बाद दोनों हवाई जहाजों के बीच की दूरी कितनी होगी?

प्र० 12. दो खंभे जिनकी ऊँचाइयाँ 6 मी. और 11 मी. हैं तथा ये समतल भूमि पर खड़े हैं। यदि इनके तलों के बीच की दूरी 12 मी. है तो इनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।

हलः माना दो खंभे AB और CD है।

खंभों के तलों के बीच की दूरी AC = 12 मी.

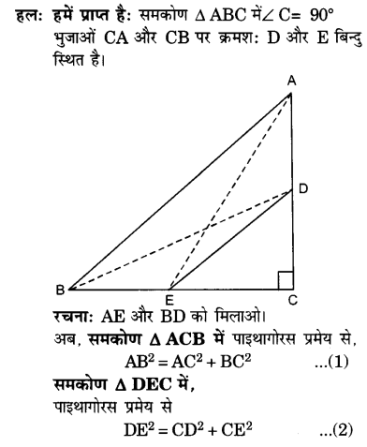
प्र० 13. किसी त्रिभुज ABC जिसका कोण C समकोण है, की भुजाओं CA और CB पर क्रमश: बिंदु D औए E स्थित है| सिद्ध कीजिए कि AE² + BD² = AB² + DE² है|

प्र० 14. किसी त्रिभुज ABC के शीर्ष A से BC पर डाला गया लंब BC को बिंदु D पर इस प्रकार प्रतिच्छेद करता है कि DB = 3CD है| सिद्ध कीजिए कि : 2AB² = 2AC² + BC² है|

प्र० 15. किसी समबाहु त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि BD = $\frac { 1 }{ 3 }$ BC है। सिद्ध कीजिए कि 9AD² = 7AB² हैं।

प्र० 16. किसी समबाहु त्रिभुज में, सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिगुना उसके एक शीर्षलंब के वर्ग के चार गुने के बराबर होता है|

हलः हमें प्राप्त है कि समबाहु ΔABC में, AD ⊥ BC

हम जानते हैं कि समबाहु A में शीर्षलम्ब संगत भुजा को समद्विभाजित करता है।

D, भुजा BC का मध्यबिन्दु है।

BD = DC [प्रत्येक = $\frac { 1 }{ 2 }$ BC]

प्र० 17. सही उत्तर चुनकर उनका औचित्य दीजिए:

ΔABC में, AB = 63 सेमी., AC = 12 सेमी. अ

BC = 6 सेमी. है। कोण B हैः

(A) 120°

(B) 60°

(C) 90°

(D) 45°

हलः हमें प्राप्त है:

AB = 6√3 सेमी.

AC = 12 सेमी.

BC = 6 सेमी.

AB² = (6√3)² = 36 x 3 = 108

AC² = 12² = 144

BC² = 6² = 36

चूंकि, 144 = 108 + 36

अर्थात् AC² = AB² + BC²

ΔABC एक समकोण त्रिभुज है जिसमें

∠B = 90° है।

अतः उत्तर (C) अर्थात् 90° सही है।

प्रश्नावली 6.6

प्र० 1. आकृति में PS कोण QPR का समद्विभाजक है| सिद्ध कीजिए कि $\frac { QS }{ SR }$ = $\frac { PQ }{ PR }$ है|

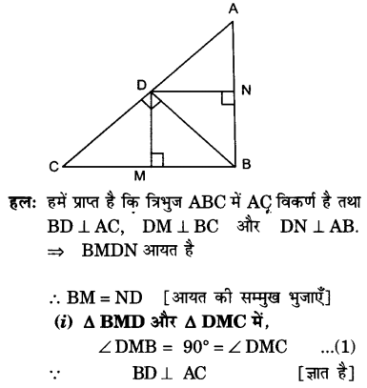
प्र० 2. आकृति में D त्रिभुज ABC के कर्ण AC पर स्थित एक बिन्दु है तथा DM ⊥ BC और DN ⊥ AB है| सिद्ध कीजिए कि

(i) DM² = DN.MC

(ii) DN² = DM.AN

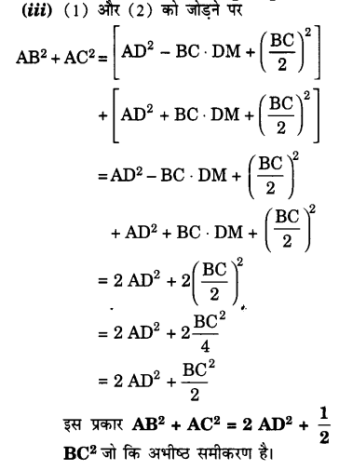
प्र० 3. आकृति में ABC एक त्रिभुज है जिसमें angle ∠ABC > 90° हा तथा AD ⊥ CB है| सिद्ध कीजिए की AC² = AB² + BC² + 2BC.BD है|

प्र० 4. आकृति में ABC एक त्रिभुज है जिसमें angle ∠ABC < 90° है तथा AD ⊥ BC है| सिद्ध कीजिए कि AC² = AB² + BC² – 2 BC.BD है|

प्र० 5. आकृति में AD त्रिभुज ABC की एक माध्यिका है तथा AM ⊥ BC है| सिद्ध कीजिए की

प्र० 6. सिद्ध कीजिए कि एक समांतर चतुर्भुज के विकार्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है|

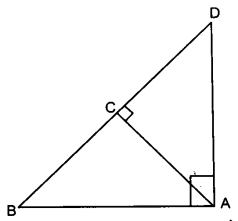
प्र० 7. आकृति में एक वृत्त की दो जिवाएँ AB और CD परस्पर बिन्दु प पर प्रतिच्छेद करती हैं| सिद्ध कीजिए कि

(i) ΔAPC ~ ΔDPB

(ii) AP.PB = CP.DP

प्र० 8. आकृति में एक वृत्त की दो जिवाएँ AB और CD बढ़ाने पर परस्पर बिन्दु P पर प्रतिच्छेद करती हैं| सिद्ध कीजिए कि

(i) ΔPAC ~ ΔPDB

(ii) PA.PB = PC.PD

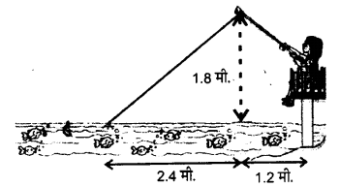
प्र० 9. आकृति में त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि $\frac { BD }{ CD }$ = $\frac { AB }{ AC }$ है| सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है |

प्र० 10. नाजिमा एक नदी की धारा में मछलियाँ पकड़ रही है| उसकी मछली पकड़ने वाली छड़ का सिरा पानी की सतह से 1.8 m ऊपर है तथा डोरी के निचले सिरे से लगा काँटा पानी के सतह पर इस प्रकार स्थित है कि उसकी नाजिमा से दुरी 3.6 m है और छड़ के सिरे के ठीक नीचे पानी के सतह पर स्थित बिन्दु से उसकी दुरी 2.4m है | यह मानते हुए कि उसकी डोरी (उसकी छड़ के सिरे से काँटे तक) तनी हुई है, उसने कितनी डोरी बाहर निकाली हुई है (देखिए आकृति 6.64)? यदि वह डोरी को 5 cm/s की दर से अन्दर खींचे, तो 12 सेकंड के बाद नाजिमा की काँटे से क्षैतिज दुरी कितनी होगी?