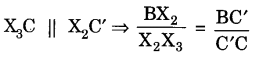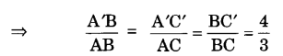NCERT Solutions Class 10 गणित Chapter-11(रचनाएँ)

Jolly November 07, 2021

NCERT Solutions Class 10 गणित Chapter-11(रचनाएँ)

NCERT Solutions Class 10  गणित  10 वीं कक्षा से Chapter-11 (रचनाएँ) के उत्तर मिलेंगे। यह अध्याय आपको मूल बातें सीखने में मदद करेगा और आपको इस अध्याय से अपनी परीक्षा में कम से कम एक प्रश्न की उम्मीद करनी चाहिए। 
हमने NCERT बोर्ड की टेक्सटबुक्स हिंदी गणित के सभी Questions के जवाब बड़ी ही आसान भाषा में दिए हैं जिनको समझना और याद करना Students के लिए बहुत आसान रहेगा जिस से आप अपनी परीक्षा में अच्छे नंबर से पास हो सके।
Solutions Class 10 गणित Chapter-11(रचनाएँ)
एनसीईआरटी प्रश्न-उत्तर

Class 10 गणित

पाठ-11 (रचनाएँ)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्नावली 11.1 

निम्न में से प्रत्येक के लिए रचना का औचित्य भी दीजिएः

प्र० 1. 7.6 सेमी. लम्बा एक रेखाखंड खींचिए और इसे 5 : 8 अनुपात में विभाजित कीजिए। दोनों भागों को मापिए।

हलः रचना के पद

I. एक रेखाखंड AB = 7.6 सेमी खींचो।

II. एक किरण AX खींचो जो AB के साथ एक न्यून कोण बनाए।

III. किरण AX पर (8 + 5) = 13 समान खंड काटो और उन्हें X1, X2, X3, X4, …, X13 से अंकित करो।

IV. X13 को B से मिलाओ।
V. X5 से X6C || X13B खींचो जो AB को C पर मिले।

Solutions Class 10 गणित Chapter-11(रचनाएँ)

इस प्रकार बिन्दु C रेखाखंड AB को 5 : 8 अनुपात में विभाजित करता है।

दोनों रेखाखंडों को मापने पर, हमें प्राप्त होता है AC = 4.7 सेमी., BC = 2.9 सेमी

Solutions Class 10 गणित Chapter-11(रचनाएँ)

प्र० 2. 4 सेमी., 5 सेमी. और 6 सेमी. भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \frac { 2 }{ 3 }गुनी हों।

Solutions Class 10 गणित Chapter-11(रचनाएँ)

रचना के पद
I. एक ΔABC की रचना इस प्रकार करो कि BC = 6 सेमी, AC = 5 सेमी और AB = 4 समी है।
II. एक किरण BX इस प्रकार खींचो की ∠CBX एक न्यून कोण हो।
III. BX पर तीन बिन्दु X1, X2, और X3 इस प्रकार अंकित करो कि
BX1 = X1 X2 = X2 X3
IV. X3 और C को मिलाओ।
V. X2 से एक रेखा X3C के समान्तर खींचो जो BC को C पर काटे।
VI. C से एक रेखा CA के समान्तर खींचो जो BA को A’ पर मिले।
इस प्रकार अभिष्ठ त्रिभुज ABC’ है।
सत्यापनः रचना से हमें प्राप्त होता है किः

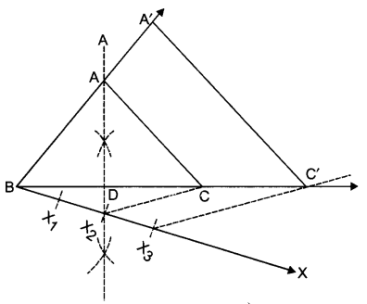
Solutions Class 10 गणित Chapter-11(रचनाएँ)

Solutions Class 10 गणित Chapter-11(रचनाएँ)

प्र० 3. 5 सेमी.,6 सेमी. और 7 सेमी. भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \frac { 7 }{ 5 }गुनी हों।

हलः

रचना के पद

I. एक त्रिभुज ABC की रचना इस प्रकार कीजिए जिसमें AB = 5 सेमी., BC = 7 सेमी. और AC = 6 सेमी. है।

Solutions Class 10 गणित Chapter-11(रचनाएँ)

II. एक किरण BX इस प्रकार खींचो की ∠CBX एक न्यून कोण हो।
III. BX पर 7 बिन्दु X1, X2, X3, X4, …, X7 अंकित करो।
IV. X5 और C को मिलाओ।
V. बिन्दु X7 से X5C || X7C’ खींचो जो BC (बढ़ाने पर) को C पर काटे।
VI. C’ से CA के समान्तर एक रेखा खींचो जो BA (बढ़ाने पर) को A’ पर काटे।
इस प्रकार ΔABC अभीष्ठ त्रिभुज है।
सत्यापनः रचना से, हमें प्राप्त होता है कि
C’A’ || CA
AA’ समरूपता से हमें प्राप्त होता है:
ΔABC ~ ΔA’B’C’

Solutions Class 10 गणित Chapter-11(रचनाएँ)

प्र० 4. आधार 8 सेमी. तथा ऊँचाई 4 सेमी. के एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ इस समद्विबाहु त्रिभुज की संगत भुजाओं की 1\frac { 1 }{ 2 }गुनी हों।

हलः

रचना के पद

I. BC = 8 सेमी खींचो।
II. BC का लम्ब समद्विभाजक खींचो जो BC को D पर काटे।
III. उक्त लम्ब पर एक बिन्दु A इस प्रकार अंकित करो कि DA = 4 सेमी.
IV. AB और AC को मिलाओ। इस प्रकार ΔABC वांछित समद्विबाहु A है।
V. अब, एक किरण BX इस प्रकार खींचो कि ∠X एक न्यून कोण हो।
VI. BX पर तीन बिन्दु X1, X2, X3 इस प्रकार
अंकित करो किः
BX1 = X1X2 = X2X3
VII. X2 और C को मिलाओ।
VIII. X3 से एक रेखा B2C के समान्तर खींचो जो BC (बढ़ाने पर) को C पर काटे।
IX. C’ से एक रेखा CA के समान्तर खींचो जो BA (बढ़ाने पर) को A’ पर काटे।
इस प्रकार ΔA’B’C’ अभीष्ठ त्रिभुज है।

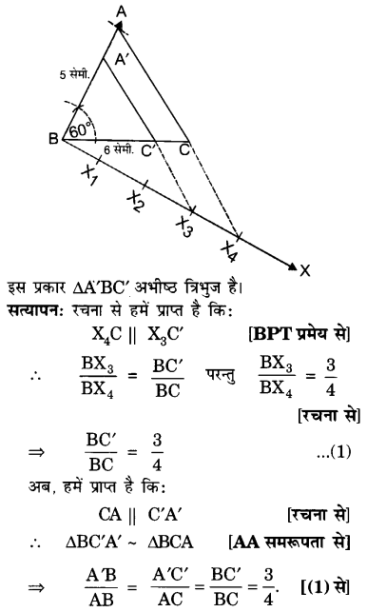
Solutions Class 10 गणित Chapter-11(रचनाएँ)

Solutions Class 10 गणित Chapter-11(रचनाएँ)

प्र० 5. एक त्रिभुज ABC बनाइए जिसमें BC = 6 सेमी, AB = 5 सेमी. और ∠ABC = 60° हो। फिर एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की \frac { 3 }{ 4 }गुनी हों। [CBSE Sample Paper2011]

हलः

रचना के पद

I. एक त्रिभुज ABC की रचना इस प्रकार करो किः BC = 6 सेमी, AB = 5 सेमी और ∠ABC = 60°.
II. एक किरण BX इस प्रकार खींचो कि ∠CBX एक न्यनू कोण हो।

III. BX पर चार बिन्दु X1, X2, X3 और X4 इस प्रकार अंकित करो कि BX1 = X1X2 = X2X3 = X3X4
IV. X4C को मिलाओ।
V. X3C’ || X4C खींचो जो कि BC को C’ पर काटे।
VI. एक अन्य रेखा C’ से CA के समान्तर खींचो जो BA को A’ पर काटे।

Solutions Class 10 गणित Chapter-11(रचनाएँ)

प्र० 6. एक त्रिभुज ABC बनाइए जिसमें BC = 7 सेमी, ∠B = 45°, ∠A = 105° हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की \frac { 4 }{ 3 }गुनी हों।

हलः

रचना के पद

Solutions Class 10 गणित Chapter-11(रचनाएँ)

I. एक ΔABC की रचना इस प्रकार करो कि BC = 7 सेमी, ∠B = 45° और ∠A = 105° हो।
II. एक किरण BX इस प्रकार खींचो कि ∠CBX एक न्यून कोण हो।
III. BX पर चार बिन्दु X1, X2, X3 और X4 इस प्रकार अंकित करो किः
BX1 = X1X2 = X2X3 = X3X4 हो।
IV. X3 और C को मिलाओ।
V. X4C’ || X3C इस प्रकार खींचो कि C’, BC (बढ़ाने पर) को मिले।
VI. C’ से CA के समान्तर एक रेखा खींचो जो BA (बढ़ाने पर) को A’ पर मिले।
इस प्रकार ΔABC अभीष्ठ त्रिभुज है।
सत्यापन: रचना से हमें प्राप्त है किः

Solutions Class 10 गणित Chapter-11(रचनाएँ)

Solutions Class 10 गणित Chapter-11(रचनाएँ)

प्र० 7. एक समकोण त्रिभुज की रचना कीजिए, जिसकी भुजाएँ (कर्ण के अतिरिक्त) 4 सेमी. तथा 3 सेमी. लम्बाई की हों। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \frac { 5 }{ 3 }गुनी हों।

हलः रचना के पद

I. एक ΔABC की रचना इस प्रकार करो कि ∠B = 90°, BC = 4 सेमी और BA = 3 सेमी हो।
II. एक किरण BX इस प्रकार खींचो कि ∠CBX एक न्यनू कोण हो।
III. BX पर पाँच बिन्दु X1, X2, X3, X4 और X5
इस प्रकार खींचो कि: BX1 = X1X2 = X2X3 = X3X4 = X4X5 हो।
IV. X3 और C को मिलाओ।
V. X5 से X3C के समान्तर एक रेखा खींचो जो BC को बढ़ाने पर C’ पर काटे।
VI. एक अन्य रेखा C’ से CA के समान्तर खींचो जो BA को बढ़ाने पर A’ पर मिले।।
इस प्रकार ΔA’B’C’ अभीष्ठ त्रिभुज है।

Solutions Class 10 गणित Chapter-11(रचनाएँ)

Solutions Class 10 गणित Chapter-11(रचनाएँ)

प्रश्नावली 11.2 

निम्न में से प्रत्येक के लिए रचना का औचित्य भी दीजिएः

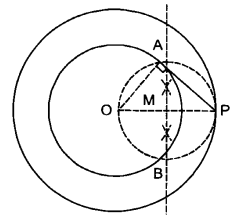
प्र० 1. 6 सेमी. त्रिज्या का एक वृत्त खींचिए। केन्द्र से 10 सेमी. दूर स्थित एक बिन्दु से वृत्त पर स्पर्श रेखा युग्म की रचना कीजिए और उनकी लम्बाइयाँ मापिए।

हलः

रचना के पद

I. एक बिन्दु 0 अंकित करो।

II. केन्द्र O और त्रिज्या 6 सेमी से एक वृत्त खींचो।

III. केन्द्र से 10 सेमी की दूरी पर एक बिन्दु P अंकित करो।

IV. O और P को मिलाओ।

V. OP को M पर समद्विभाजित करो।

VI. बिन्दु M को केन्द्र लेकर MO या MP के समान त्रिज्या से एक वृत्त खींचो जो दिए गये वृत्त को A और B पर काटे।

VII. PA और PB को मिलाओ। इस प्रकार, PA और PB दो अभिष्ठ स्पर्श रेखाएँ हैं। मापने पर, PA = PB = 9.6 सेमी.

Solutions Class 10 गणित Chapter-11(रचनाएँ)

सत्यापनः OA और OB को मिलाओ चूँकि OP एक व्यास है।

∠OAP = 90°; ∠OBP = 90° [अर्धवृत्त में बने कोण]

पुनः OA और OB एक ही वृत्त की त्रिज्याएँ हैं।

PA और PB वृत्त पर स्पर्श रेखाएँ है।

प्र० 2. 4 सेमी. त्रिज्या के एक वृत्त पर 6 सेमी. त्रिज्या के एक सकेन्द्रीय वृत्त के किसी बिन्दु से एक स्पर्श रेखा की रचना कीजिए और उसकी लम्बाई मापिए। परिकलन से इस माप की जाँच भी कीजिए।

हलः

रचना के पद

I. 4 सेमी और 6 सेमी त्रिज्या के दो वृत्त एक ही केन्द्र O से खींचो।

II. बड़े वृत्त पर एक बिन्दु P अंकित करो।

III. O और P को मिलाओ।

IV. OP का लम्ब समद्विभाजक M ज्ञात करो।

V. Mको केन्द्र और OM या PM के समान त्रिज्या से एक वृत्त खींचो जो छोटे वृत्त को A और B पर काटे।

VI. A और P को मिलाइए।

इस प्रकार PA अभीष्ठ स्पर्श रेखा है। मापने पर, PA = 4.5 सेमी

Solutions Class 10 गणित Chapter-11(रचनाएँ)

सत्यापनः O और A को मिलाओ।

∠PAO = 90° [अर्धवृत्त में बना कोण]

PA ⊥ OA

OA, छोटे वृत्त की त्रिज्या है।

छोटे वृत्त पर PA एक स्पर्श रेखा है।

प्र० 3. 3 सेमी, त्रिज्या का एक वृत्त खींचिए। इसके किसी बढ़ाए गए व्यास पर केन्द्र से 7 सेमी. की दूरी पर स्थित दो बिन्दु P और Q लीजिए। इन दोनों बिन्दुओं से वृत्त पर स्पर्श रेखाएँ खींचिए।

हलः

रचना के पद

I. केन्द्र O और त्रिज्या 3 सेमी का एक वृत्त खींचो।

II. उक्त वृत्त के व्यास को बढ़ाकर, इस पर दो बिन्दु P और 9 इस प्रकार अंकित कीजिए किः

OP = OQ = 7 सेमी

III. OP और OQ के मध्य बिन्दु क्रमश: M1 और M2 ज्ञात कीजिए।

Solutions Class 10 गणित Chapter-11(रचनाएँ)

IV. M1 को केन्द्र व M1P को त्रिज्या मानकर एक वृत्त खींचो जो वृत्त को A और B पर काटे।
V. PA और PB को मिलाओ। PA और PB अभीष्ठ स्पर्श रेखाएँ हैं।
VI. अब OQ के मध्य बिन्दु M2 और M2O के समान त्रिज्या लेकर वृत्त खींचो जो दिए गये वृत्त को C और D पर काटे।

VII. OC और OD को मिलाओ। इस प्रकार OQ और QD अभीष्ट स्पर्श रेखाएँ हैं।
सत्यापनः OA को मिलाओ।
∠OAP = 90°
PA ⊥ OA
PA एक स्पर्श रेखा है।
इस प्रकार, PB ⊥OA
PB एक स्पर्श रेखा है।
अब, OC को मिलाने पर
∠OCQ = 90°
QC ⊥ OC
QC एक स्पर्श रेखा है।
इसी प्रकार, QD ⊥ OC = QD एक स्पर्श रेखा है।

प्र० 4. 5 सेमी, त्रिज्या के एक वृत्त पर ऐसी दो स्पर्श रेखाएँ खींचिए, जो परस्पर 60° के कोण पर झुकी हों।

हलः

रचना के पद

I. केन्द्र O और त्रिज्या = 5 सेमी से दिये गये वृत्त की रचना करो।

II. ∠AOB = 120° बनाओ।

III. बिन्दु A से OA पर एक लम्ब खींचो।

IV. B से एक लम्ब OB पर खींचो।

V. उक्त लम्बों को C पर मिलने दो।

इस प्रकार CA तथा CB वृत्त की अभीष्ठ स्पर्श रेखाएँ है, जो परस्पर 60° पर झुकी हुई हैं।

Solutions Class 10 गणित Chapter-11(रचनाएँ)

सत्यापनः चतुभुर्ज OACB में, कोण-योग-गुण से

120° + 90° + 90° + ∠ACB = 360°

⇒ 300° + ∠ACB = 360°

⇒ ∠ACB = 360° – 300° = 60°

प्र० 5. 8 सेमी. लम्बा एक रेखाखंड AB खींचिए। A को केन्द्र मानकर 4 सेमी. त्रिज्या का एक वृत्त तथा B को केन्द्र लेकर 3 सेमी, त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केन्द्र से स्पर्श रेखाओं की रचना कीजिए।

हलः

रचना के पद

I. A और B को मिलाओ।

II. AB का लम्बसमद्विभाजक ज्ञात करो। माना AB का मध्य बिन्दु M है।

III. केन्द्र M और त्रिज्या = MA या MB लेकर एक वृत्त खींचो जो केन्द्र A वाले वृत्त को P और Q पर काटे, तथा केन्द्र B वाले वृत्त को R और S पर काटे।

IV. BP और BQ को मिलाओ। इस प्रकार, BP तथा BQ केन्द्र A वाले वृत्त पर B से अभीष्ठ स्पर्श रेखाएँ है।

V. अब, RA और SA को मिलाओ।

इस प्रकार, केन्द्र B वाले वृत्त पर A से स्पर्श रेखाएँ RA तथा SA हैं।

Solutions Class 10 गणित Chapter-11(रचनाएँ)

सत्यापनः A और P को मिलाने पर,

∠APB = 90°

BP ⊥ AP

परन्तु AP, केन्द्र A वाले वृत्त की त्रिज्या है।

केन्द्र A वाले वृत्त पर AP एक स्पर्श रेखा है।

इसी प्रकार, BQ भी केन्द्र A वाले वृत्त पर एक स्पर्श रेखा है। केन्द्र B वाले वृत्त पर भी उक्त प्रकार से AR और AS स्पर्श रेखाएँ हैं।

प्र० 6. माना ABC एक समकोण त्रिभुज है, जिसमें AB = 6 सेमी., BC = 8 सेमी. तथा ∠B = 90° है। B से AC पर BD लम्ब है। बिन्दुओं B, C, D से होकर जाने वाला एक वृत्त खींचा गया है। A से इस वृत्त पर स्पर्श रेखा की रचना कीजिए।

हलः रचना के पद

I. AB = 6 सेमी, BC = 8 सेमी तथा ∠B = 90° मापों से ΔABC की रचना करो।

II. BD ⊥ AC खींचो।

III. B, C और D से होकर एक वृत्त खींचो।

IV. AO को मिलाओ।

V. AO को M पर समद्विभाजित करो।

VI. केन्द्र M और त्रिज्या MA लेकर एक वृत्त खींचो जो दिये गये वृत्त को B और E पर काटता है।

VII. AB और AE को मिलाओ।

इस प्रकार बिन्दु A से दिए गये वृत्त पर AB और AE स्पर्श रेखाएँ हैं।

Solutions Class 10 गणित Chapter-11(रचनाएँ)

सत्यापनः OE को मिलाने पर,

∠AEO = 90° [अर्धवृत्त में बनी कोण]

AE ⊥ OE

परन्तु OE, दिए गये वृत्त की एक त्रिज्या है।

AE वृत्त की एक स्पर्श रेखा है।

इसी प्रकार, AB भी दिए गये वृत्त की एक स्पर्श रेखा है।

प्र० 7. किसी चूड़ी की सहायता से एक वृत्त खींचिए। वृत्त के बाहर एक बिन्दु लीजिए। इस बिन्दु से वृत्त पर स्पर्श रेखाओं की रचना कीजिए।

हलः रचना के पद

I. चूड़ी की सहायता से दिए गये वृत्त की रचना करो।

II. दिए गये वृत्त में दो असमान्तर जीवाएँ PQ और RS खींचो।

III. P और RS के लम्बसमद्विभाजक खींचो जो परस्पर बिन्दु O पर प्रतिच्छेद करे। इस प्रकार बिन्दु O दिए गये वृत्त का केन्द्र है।

IV. दिए गये वृत्त के बाहर एक बिन्दु P लो।

V. OP को मिलाओ।

VI. OP का मध्य बिन्दु M अंकित करो।

VII. केन्द्र M और त्रिज्या-OM से एक वृत्त खींचो, जो दिए गये वृत्त को A और B पर काटे।।

VIII. PA और PB को मिलाओ।

इस प्रकार PA और PB स्पर्श रेखाएँ हैं।

Solutions Class 10 गणित Chapter-11(रचनाएँ)

सत्यापनः OA और OB को मिलाने पर,

∠OAP = 90°, ∠OBP = 90° [अर्धवृत्त में बने कोण]

PA ⊥ OA तथा PB ⊥ OB

PA, दिए गये वृत्त पर एक स्पर्श रेखा है तथा PB, दिए गये वृत्त पर दूसरी स्पर्श रेखा है।

एनसीईआरटी सोलूशन्स क्लास 10 गणित पीडीएफ

Tags: