NCERT Solutions Class 10 गणित Chapter-10 (वृत्त)
Class 10 गणित
पाठ-10 (त्रिकोणमिति के कुछ अनुप्रयोग)
अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर
प्रश्नावली 10.1
प्र० 1. एक वृत्त की कितनी स्पर्श रेखाएँ हो सकती हैं?
हलः एक वृत्त की अनगिनत स्पर्श-रेखाएँ हो सकती हैं।
प्र० 2. रिक्त स्थानों की पूर्ति कीजिएः
(i) किसी वृत्त की स्पर्श रेखा उसे बिंदु ………….. पर प्रतिच्छेद करती है।
(ii) वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा को …………. कहते हैं।
(iii) एक वृत्त की ………….. समांतर स्पर्श रेखाएँ हो सकती हैं।
(iv) वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिंदु को ………….. कहते हैं।
हलः
(i) केवल एक
(ii) छेदक-रेखा
(iii) दो।
(iv) स्पर्श बिन्दु
प्र० 3. 5 सेमी त्रिज्या वाले एक वृत्त के बिंदु P पर स्पर्श रेखा PQ केंद्र 0 से जाने वाली एक रेखा से बिंदु Q पर इस प्रकार मिलती है कि OQ = 12 सेमी। PQ की लंबाई है।
(A) 12 सेमी.
(B) 13 सेमी.
(C) 8.5 सेमी.
(D) √119 सेमी.
हलः चूंकि वृत्त के किसी बिन्दु पर स्पर्श रेखा स्पर्श बिन्दु से जाने वाली त्रिज्या पर लम्ब होती है।
प्र० 4. एक वृत्त खींचिए और एक दी गई रेखा के समांतर दो ऐसी रेखाएँ खींचिए कि उनमें से एक स्पर्श रेखा हो तथा दूसरी छेदक रेखा हो।
हलः वांछित आकृति नीचे दर्शाई गई है। इसमें O वृत्त का केन्द्र है।
(i) रेखा l दी गई रेखा है।
(ii) PT और AB दोनों l के समान्तर हैं।
(iii) PT बिन्दु P पर एक स्पर्श रेखा है।
(iv) AB वृत्त की छेदक रेखा है।
प्रश्नावली 10.2
प्रश्न सं. 1,2,3 में सही विकल्प चुनिए एवं उचित कारण दीजिए।
प्र० 1. एक बिंदु Q से एक वृत्त पर स्पर्श रेखा की लंबाई 24 सेमी. तथा Q की केंद्र से दूरी 25 सेमी. है। वृत्त की त्रिज्या है:
(A) 7 सेमी.
(B) 12 सेमी.
(C) 15 सेमी.
(D) 24.5 सेमी.
हलः चूंकि O वृत्त का केन्द्र और QT एक स्पर्श रेखा है।
प्र० 2. आकृति में, यदि TP, TQ केंद्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠POQ = 110°, तो ∠PTQ बराबर हैं:
(A) 60°
(B) 70°
(C) 80°
(D) 90°
हलः आकृति में O वृत्त का केन्द्र है, बाह्य बिन्दु T से दो स्पर्श रेखाएँ TP और TQ इस प्रकार हैं कि
∠POQ = 110°
OP ⊥ PT और OQ ⊥ QT
⇒ ∠OPT = 90° और ∠OQT = 90°
अब, चतुर्भुज TPOQ में, हमें प्राप्त है:
∠PTQ + 90° + 110° + 90° = 360°
⇒ ∠PTQ + 290° = 360°
⇒ ∠PTQ = 360° – 290° = 70°
इस प्रकार विकल्प (B) सही है।
प्र० 3. यदि एक बिंदु P से O केंद्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर 80° के कोण पर झुकी हों, तो ∠POA बराबर हैः
(A) 50°
(B) 60°
(C) 70°
(D) 80°
हलः चूंकि, वृत्त का केन्द्र O और P से वृत्त की दो स्पर्श रेखाएँ PA और PB हैं:
OA ⊥ AP और OB ⊥ BP
∠OAP = ∠OBP = 90°
अब, चतुर्भुज PAOB में, हमें प्राप्त है:
∠APB + ∠PAO + ∠AOB + ∠PBO = 360°
⇒ 80° + 90° + ∠AOB + 90° = 360°
⇒ 260° + ∠AOB = 360°
⇒ ∠AOB = 360° – 260°
⇒ ∠AOB = 100°
अब, समकोण ∆OAP तथा समकोण ∆OBP में,
OP = OP [उभयनिष्ठ]
∠OAP = ∠OBP [प्रत्येक = 90°]
OA = OB [एक ही वृत की त्रिज्याएँ]
∆OAP = ∆OBP [SAS]
इनके संगत-अंग समान होंगे।
∠POA = ∠POB
⇒ ∠POA = ∠AOB =
x 100° = 50°
इस प्रकार, विकल्प (A) सही है।
प्र० 4. सिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समांतर होती हैं।
आकृति में, हमें प्राप्त है कि: वृत का केन्द्र O और PQ एक व्यास है। माना AB और CD वृत्त के व्यास PQ के सिरों पर खींची गई स्पर्श रेखाएँ हैं।
चूंकि स्पर्श-बिन्दु से होकर खींची गई त्रिज्या वृत्त की स्पर्श-रेखा पर लम्ब होती है।
PQ ⊥ AB
∠APQ = 90° …..(1)
और
PQ ⊥ CD
∠PQD = 90° ………(2)
(1) और (2) से,
∠APQ = ∠PQD
परन्तु ये संगत कोणों का एक युग्म बनाते हैं। |
AB || CD
प्र० 5. सिद्ध कीजिए कि स्पर्श बिंदु से स्पर्श रेखा पर खींचा गया लंब वृत्त के केंद्र से होकर जाता है।
आकृति में, O, वृत्त का केन्द्र और स्पर्श रेखा AB वृत्त को बिन्दु P पर स्पर्श करती है। OP को मिलाओ।
चूंकि स्पर्श-बिन्दु से होकर खींची गई त्रिज्या वृत्त की स्पर्श-रेखा पर लम्ब होती है।
AB ⊥ OP
∠OPB = 90° ……..(1)
यदि सम्भव हो, तो PQ ⊥ AB खींचिए जो कि O से नहीं गुजरता है।
AB ⊥ OP
∠QPB = 90° ………(2)
(1) और (2) से,
∠QPB = ∠OPB
यह तभी संभव है, जब O और Q संपाती हो। इस प्रकार, हम कह सकते हैं कि:
स्पर्श रेखा पर स्पर्श बिन्दु से खींचा गया लम्ब, वृत्त के केन्द्र से होकर जाता है।
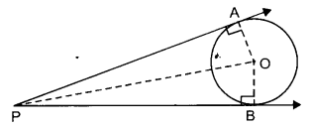
प्र० 6. एक बिंदु A से, जो वृत्त के केंद्र से 5 सेमी. दूरी पर है, वृत्त पर स्पर्श रेखा की लंबाई 4 सेमी. है। वृत्त की त्रिज्या ज्ञात कीजिए।
हलः
चूंकि वृत्त के किसी बिन्दु पर स्पर्श रेखा स्पर्श बिन्दु से जाने वाली त्रिज्या पर लम्ब होती है।
∠OTA = 90°
समकोण ΔOTA में हमें प्राप्त है:
⇒ OA² = OT² + AT²
⇒ 5² = OT² + 4²
⇒ OT² = 5² – 4²
⇒ OT² = (5 – 4) (5 + 4)
⇒ OT² = 1 x 9 = 9 = 3²
⇒ OT = 3
इस प्रकार, वृत्त की त्रिज्या 3 सेमी है।
प्र० 7. दो संकेंद्रीय वृत्तों की त्रिज्याएँ 5 सेमी. तथा 3 सेमी. हैं। बड़े वृत्त की उस जीवा की लंबाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो।
हलः
आकृति में, O दोनों वृत्तों का उभयनिष्ठ केन्द्र है।
बड़े वृत्त की जीवा AB इस प्रकार है कि यह छोटे वृत्त की P पर स्पर्श रेखा है।
⇒ OP ⊥ AB = ∠OPB = 90°
हम यह भी जानते हैं कि स्पर्श-बिन्दु से जाने वाली त्रिज्या स्पर्श रेखा पर लम्ब होती है।
AB को OP समद्विभाजित करता है।
⇒ AP = AB
समकोण ΔAPO में,
⇒ OA² = AP² – OP²
⇒ 5² = AP² – 3²
⇒ AP² = 5² – 3²
⇒ AP² = (5 – 3) (5 + 3) = 2 x 8
⇒ AP² = 16 = (4)²
⇒ AP = 4 सेमी.
AB = 4
⇒ AB = 2 x 4 = 8 सेमी.
अत: जीवा AB की अभीष्ठ लम्बाई 8 सेमी.
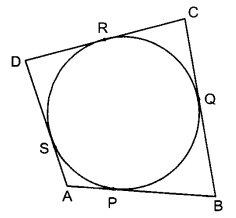
प्र० 8. एक वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है (देखिए आकृति)। सिद्ध कीजिएः
AB + CD = AD + BC [AI CBSE 2008 C]
हलः चूंकि चतुर्भुज ABCD की भुजाएँ AB, BC, CD
और DA वृत्त को बिन्दुओं P, Q, R और S पर स्पर्श करती हैं।
और एक बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाएँ समान होती हैं।
AP= AS
BP = BQ
DR = DS
CR = CQ
उक्त समीकरणों को जोड़ने पर हमें प्राप्त होता है।
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CG)
⇒ AB + CD = AD+ BC
यही सिद्ध करना था।
प्र० 9. आकृति में XY तथा X’Y’, O केंद्र वाले किसी वृत्त पर दो समांतर स्पर्श रेखाएँ हैं और स्पर्श बिंदु C पर स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर प्रतिच्छेद करती है। सिद्ध कीजिए कि ∠AOB = 90° है।
हलः चूंकि एक बाह्य बिन्दु से वृत्त पर खींची गयी स्पर्श-रेखाएँ समान होती है।
AP = AC
ΔPAO और ΔAOC में, हमें प्राप्त है।
AO = AO [उभयनिष्ठ]
OP = OC [एक ही वृत्त की त्रिज्याएँ]
AP = AC [बिन्दु A से वृत पर स्पर्श रेखाएँ]
ΔPAO = ΔAOC [SSS सर्वांगसमता]
∠PAO = ∠CAO
∠PAC = 2 ∠CAO ….(1)
इसी प्रकार, ∠CBQ = 2∠CBO …….(2)
हम यह भी जानते हैं कि यहाँ तिर्यक रेखा AB के एक ही ओर के अन्तः कोणों का योग 180° होगा।
∠PAC + ∠CBQ = 180°
या 2 ∠CA0 + 2 ∠CBO = 180° [ (1) और (2) से ]
∠CAO + ∠CBO = 90° …..(3)
अब ΔAOB में,
∠BAO + ∠ABO + ∠AOB = 180°
या ∠CAO + ∠CBO + ∠AOB = 180°
∠BAO और ∠CAO एक ही कोण है।
तथा ∠ABO और ∠CAO एक कोण है।
90° + ∠AOB = 180° [(3) से]
∠AOB = 180° – 90° = 90°
अतः
∠AOB = 90°
प्र० 10. सिद्ध कीजिए कि किसी बाह्य बिंदु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिंदुओं को मिलाने वाले रेखाखंड द्वारा केंद्र पर अंतरित कोण का संपूरक होता है।
हलः
माना PA और PB दो स्पर्श रेखाएँ हैं जो कि वृत्त पर बाह्य बिन्दु P पर खींची गई है। वृत्त का केन्द्र O बिन्दु पर है।
अब, समकोण ΔOAP और A OBP में, हमें प्राप्त है कि:
PA = PB [बाह्य बिन्दु से वृत्त पर स्पर्श-रेखाएँ]
OA = OB [एक ही वृत्त की त्रिज्याएँ]
OP = OP [उभयनिष्ठ]
SSS सर्वांगसमता से,
ΔΟΑΡ = ΔOPB इनके संगत भाग भी समान होंगे।
⇒ ∠OAA = ∠OPB
और ∠AOP = ∠BOP
∠APB = 2 ∠OPA
और ∠AOB = 2∠AOP
परन्तु ∠AOP = 90° – ∠OPA
2∠AOP = 180° – 2∠OPA
⇒ ∠AOB = 180° – ∠APB
⇒ ∠AOB + ∠APB = 180°
प्र० 11. सिद्ध कीजिए कि किसी वृत्त के परिगत समांतर चतुर्भुज समचतुर्भुज होता है।
हलः
हमें प्राप्त है कि समान्तर चतुर्भुज ABCD उस वृत्त को परिगत करता है (अर्थात् इसकी भुजाएँ उस वृत्त को स्पर्श करती हैं), जिसका केन्द्र O है।
चूंकि, इस बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाई समान होती है।
AP = AS
BP = BQ
CR = CQ
DR = DS
जोड़ने पर।
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
⇒AB + CD = AD + BC
परन्तु AB = CD [च.भु. ABCD की भुजाएँ]
और BC = AD
⇒ AB + CD = AD + BC
⇒ 2 AB = 2 BC
⇒ AB = BC
इसी प्रकार AB = DA और DA = CD
अतः AB = BC = CD = AD
ABCD एक समचर्तुभुज है।
प्र० 12. 4 सेमी, त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखंड BD और DC (जिनमें स्पर्श बिंदु D द्वारा BC विभाजित है) की लंबाइयाँ क्रमशः 8 सेमी. और 6 सेमी. हैं (देखिए आकृति)। भुजाएँ AB और AC ज्ञात कीजिए।
हलः यहाँ, वृत्त को केन्द्र O तथा त्रिज्या 4 सेमी. है।
इसके परिगत एक ΔABC है।
चूंकि Δ की भुजाएँ BC, CA और AB वृत्त को क्रमश: D, E और F पर स्पर्श करती हैं।
BF = BD = 8 सेमी.
CF = CD = 6 सेमी.
AF = AE = x सेमी. (माना)
Δ की भुजाएँ इस प्रकार हैं:
14 सेमी., (x + 6) सेमी. और (x + 8) सेमी.
ΔABC का परिमाप = [14 + (x + 6) + (x + 8)] सेमी. = [14 + 6 + 8 + 2x] सेमी. = 28 + 2x सेमी.
परन्तु = = (-14) अवांछनीय है।
x = 7 सेमी.
इस प्रकार, AB = 8 + 7 = 15 सेमी.,
BC = 8 + 6 = 14 सेमी.,
CA = 6 + 7 = 13 सेमी.
प्र० 13. सिद्ध कीजिए कि वृत्त के परिगत बनी चतुर्भुज की आमने-सामने की भुजाएँ केंद्र पर संपूरक कोण अंतरित करती हैं।
हलः हमें प्राप्त है कि वृत्त जिसका केन्द्र O है, के परिगत चतुर्भुज ABCD है।
चतुर्भुज की भुजाएँ AB, BC, CD और DA वृत्त को क्रमशः P, Q, R और S पर स्पर्श करती हैं। हम जानते हैं कि बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाएँ, केन्द्र पर समान कोण बनाती हैं।
∠1 = ∠2,
∠3 = ∠4
∠5 = ∠6
और ∠7 = ∠8
एक बिन्दु पर बने सभी कोणों का योग 360° होता है।
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
⇒ 2(∠1 + ∠8 + ∠5 + ∠4) = 360°
(∠1 + ∠ 8 + ∠5 + ∠4) = 180° …(1)
और 2(∠2 + ∠3 + ∠6 + ∠7) = 360°
⇒ (∠2 + ∠3) + (∠6 + ∠7) = 180° …(2)
चूंकि
∠2 + ∠3 = ∠AOB
∠6 + ∠7 = ∠COD
∠1 + ∠8 = ∠AOD
∠4 + ∠5 = ∠BOC
(1) और (2) से हमें प्राप्त होता है।
∠AOD + ∠BOC = 180°
और ∠AOB + ∠COD = 180°