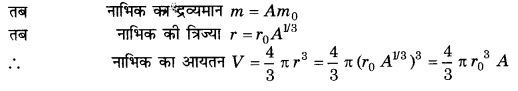NCERT Solutions Class 11 भौतिकी विज्ञान Chapter-2 (मात्रक एवं मापन)

NCERT Solutions Class 11 भौतिकी विज्ञान 11 वीं कक्षा से Chapter-2 (मात्रक एवं मापन) के उत्तर मिलेंगे। यह अध्याय आपको मूल बातें सीखने में मदद करेगा और आपको इस अध्याय से अपनी परीक्षा में कम से कम एक प्रश्न की उम्मीद करनी चाहिए। 

हमने NCERT बोर्ड की टेक्सटबुक्स हिंदी  भौतिकी विज्ञान के सभी Questions के जवाब बड़ी ही आसान भाषा में दिए हैं जिनको समझना और याद करना Students के लिए बहुत आसान रहेगा जिस से आप अपनी परीक्षा में अच्छे नंबर से पास हो सके।

एनसीईआरटी प्रश्न-उत्तर

Class 11 (भौतिकी विज्ञान )

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

पाठ-2 (मात्रक एवं मापन)

प्रश्न 1:

रिक्त स्थान भरिए

(a) किसी 1 cm भुजा वाले घन का आयतन…..m³ के बराबर है।

(b) किसी 2 cm त्रिज्या व 10 cm ऊँचाई वाले सिलिण्डर का पृष्ठ क्षेत्रफल…..(mm)² बराबर है।

(c) कोई गाड़ी 18 kmem/h की चाल से चल रही है तो यह 1s में….m चलती है।

(d) सीसे का आपेक्षिक घनत्व 11.3 है। इसका घनत्व….g cm^-3 या …. kg m^-3 है।

उत्तर :

(a) ∵ घन का आयतन = ( भुजा)³ =(1 cm)³
= (m)³ = (10-2 m)³ [ 1cm== 10^-2 m)
=10^-6 m³

(b) सिलिण्डर का पृष्ठ क्षेत्रफल = वक्र पृष्ठ का क्षेत्रफल + दोनों वृत्तीय सिरों का क्षेत्रफल

=2πrh + 2πr²
= 2π (h +r)= 2x 3.14 x 2 cm (10 cm + 2 cm)
= 4 x 3:4 x 12cm² = 150.72 cm²
= 150.72 x (10mm)² (∵1 cm = 10 mm)
= 150.72 x 100(mm)² =1.5x 104 (mm)²

(c) गाड़ी की चाल = 18km/h

= 18x m/s = 5 m s^-1
∴ 1s में तय दूरी = चाल x समय = 5ms^-1 x1 s=5 m

(d) सीसे का घनत्व = सीसे का आपेक्षिक-घनत्व x जल का घनत्व

= 11.3 x 1 g cm^-3 = 11.3 g cm^-3
[∵जल का घनत्व = 1 g cm^-3 या 10 kg m^-3]
या   सीसे का घनत्व = 11.3 x 10³ kg m^-3
= 1.13 x 104 kg m^-3

प्रश्न 2:

रिक्त स्थानों को मात्रकों के उचित परिवर्तन द्वारा भरिए

(a) 1 kg m² s^-2= ……g cm² s^-2
(b) 1 m = …. 1y
(c) 3.0 m s^-2 = …. km h^-2
(d) G= 6.67x 10^-11 Nm (kg)^-2 =……… (cm)3 s^-2 g^-1

उत्तर :

(a) 1 kg m²s^-2 = 1 kg x 1m²s^-2
= (1000 g)x (100 cm)2x 1s^-2
= 1000 x 10000 g (cm)2 s^-2
= 10⁷g (cm)2 s^-2

प्रश्न 3:

ऊष्मा या ऊर्जा का मात्रक कैलोरी है और यह लगभग 4.2J के बराबर है, जहाँ 11J =1 kg m² s^-2 मान लीजिए कि हम मात्रकों की कोई ऐसी प्रणाली प्रयोग करते हैं जिसमें द्रव्यमान का मात्रक α kg के बराबर है, लम्बाई का मात्रक β m के बराबर है, समय का मात्रक γs के बराबर है तो यह प्रदर्शित कीजिए कि नए मात्रकों के पदों में कैलोरी का परिमाण 4.2 α^-1 β^-2 γ² है।

उत्तर :

1 कैलोरी = 4.2.J = 4.2 kg-m²S^-2
ऊर्जा का विमीय सूत्र = [ML²F^-2]

माना दी गई दो मापन पद्धतियों में द्रव्यमान, लम्बाई तथा समय के मात्रक क्रमशः M₁,L₁, T₁, तथा M₂,L₂, T₂, हैं। 

प्रश्न 4:

इस कथन की स्पष्ट व्याख्या कीजिए : तुलना के मानक का विशेष उल्लेख किए बिना “किसी विमीय राशि को ‘बड़ा या छोटा कहना अर्थहीन है।” इसे ध्यान में रखते हुए नीचे दिए गए कथनों को जहाँ कहीं भी आवश्यक हो, दूसरे शब्दों में व्यक्त कीजिए

(a) परमाणु बहुत छोटे पिण्ड होते हैं।

(b) जेट वायुयान अत्यधिक गति से चलता है।

(c) बृहस्पति का द्रव्यमान बहुत ही अधिक है।

(d) इस कमरे के अन्दर वायु में अणुओं की संख्या बहुत अधिक है।

(e) इलेक्ट्रॉन, प्रोटॉन से बहुत भारी होता है।

(f) ध्वनि की गति प्रकाश की गति से बहुत ही कम होती है।

उत्तर :

सामान्यतया कहा जाता है कि परमाणु बहुत छोटा गोलीय पिण्ड है, परन्तु हम जानते हैं कि इलेक्ट्रॉन परमाणु से भी छोटा कण है, तब यह कहा जा सकता है कि इलेक्ट्रॉन की तुलना में परमाणु एक बड़ा पिण्ड है। इसके विपरीत क्रिकेट की गेंद की तुलना में परमाणु एक बहुत छोटा पिण्ड है। इस प्रकार हम देखते हैं कि परमाणु को किसी एक वस्तु की तुलना में बहुत छोटा कहा जा सकता है जबकि किसी अन्य वस्तु की तुलना में उसे बड़ा कहा जा सकता है। यही बात किसी विमीय राशि के विषय में भी लागू होती है। कोई विमीय राशि, किसी दूसरी समान विमीय राशि की तुलना में बड़ी हो सकती है जबकि किसी अन्य, समान विमीय राशि से छोटी हो सकती है। अत: किसी विमीय राशि को छोटा या बंड़ा कहना तब तक अर्थहीन है जब तक कि तुलना के मानक को स्पष्ट उल्लेख ने किया गया हो।

(a) चीनी के एक दाने की तुलना में परमाणु बहुत छोटे पिण्ड होते हैं।

(b) जेट वायुयान, रेलगाड़ी की तुलना में अत्यधिक गति से चलता है।

(c) बृहस्पति का द्रव्यमान, पृथ्वी के द्रव्यमान की तुलना में बहुत ही अधिक है।

(d) इस कमरे के अन्दर वायु में अणुओं की संख्या, एक ग्राम-अणु गैस में उपस्थित अणुओं की संख्या ‘ से बहुत अधिक है। कथनों

(e) तथा

(f) को बदलने की आवश्यकता नहीं है।

प्रश्न 5:

लम्बाई का कोई ऐसा नया मात्रक चुना गया है जिसके अनुसार निर्वात में प्रकाश की चाल 1 है। लम्बाई के नए मात्रक के पदों में सूर्य तथा पृथ्वी के बीच की दूरी कितनी है, प्रकाश इस दूरी को तय करने में 8 min और 20 s लगाता है।

उत्तर :

प्रकाश की चाल = 1 मात्रक S^-1
जबकि प्रकाश द्वारा लिया गया समय है t = 8 min 20 s
= (8x 60 + 20) s = 500s
∴ सूर्य तथा पृथ्वी के बीच की दूरी = प्रकाश की चाल x लगा समय
=1 मात्रक s^-1 x 500 s

= 500 मात्रक

प्रश्न 6:

लम्बाई मापने के लिए निम्नलिखित में से कौन-सा सबसे परिशुद्ध यन्त्र है

(a) एक वर्नियर कैलीपर्स जिसके वर्नियर पैमाने पर 20 विभाजन हैं।

(b) एक स्क्रूगेज जिसका चूड़ी अन्तराल 1 mm और वृत्तीय पैमाने पर 100 विभाजन हैं।

(c) कोई प्रकाशिक यन्त्र जो प्रकाश की तरंगदैर्घ्य की सीमा के अन्दर लम्बाई माप सकता है।

उत्तर :

प्रश्न 7:

कोई छात्र 100 आवर्धन के एक सूक्ष्मदर्शी के द्वारा देखकर मनुष्य के बाल की मोटाई मापता है। वह 20 बार प्रेक्षण करता है और उसे ज्ञात होता है कि सूक्ष्मदर्शी के दृश्य क्षेत्र में बाल की औसत मोटाई 3.5 mm है। बाल की मोटाई का अनुमान क्या है?

उत्तर :

प्रश्न 8.

निम्नलिखित के उत्तर दीजिए

(a) आपको एक धागा और मीटर पैमाना दिया जाता है। आप धागे के व्यास का अनुमान किस प्रकार लगाएँगे?

(b) एक स्क्रूगेज का चूड़ी अन्तराल 1.0 mm है और उसके वृत्तीय पैमाने पर 200 विभाजन हैं। क्या आप यह सोचते हैं कि वृत्तीय पैमाने पर विभाजनों की संख्या स्वेच्छा से बढ़ा देने पर स्क्रूगेज की यथार्थता में वृद्धि करना संभव है?

(c) वर्नियर कैलीपर्स द्वारा पीतल की किसी पतली छड़ का माध्य व्यास मापा जाना है। केवल 5 मापनों के समुच्चय की तुलना में व्यास के 100 मापनों के समुच्चय के द्वारा अधिक विश्वसनीय अनुमान प्राप्त होने की सम्भावना क्यों है?

उत्तर :

(a) इसके लिए हम एक बेलनाकार छड के ऊपर धागे को इस प्रकार लपेटेंगे कि धागे के फेरे एक-दूसरे से सटे रहें। धागे के फेरों द्वारा घेरी गई छड़ की लम्बाई l को मीटर पैमाने की सहायता से नाप लेंगे। अब लपेटे गए फेरों की संख्या n को गिन लिया जाएगा।

प्रश्न 9:

किसी मकान का फोटोग्राफ 35 mm स्लाइड पर 1.75 cm ² क्षेत्र घेरता है। स्लाइड को | किसी स्क्रीन पर प्रक्षेपित किया जाता है और स्क्रीन पर मकान का क्षेत्रफल 1.55 m2 है। प्रक्षेपित्र-परदा व्यवस्था का रेखीय आवर्धन क्या है?

उत्तर :

स्लाइड पर मकान का क्षेत्रफल = 1.75 cm²

स्क्रीन पर मकान का क्षेत्रफल = 1.55 m2 = 1.55 (100 cm)

= 1.55x 10000 cm²

प्रश्न 10:

निम्नलिखित में सार्थक अंकों की संख्या लिखिए

(a) 0.007 m²
(b) 2.64 x 10²⁴ kg
(c) 0.2370 cm^-3
(d) 6.320 J
(e) 6.032 Nm^-2
(f) 0.000603² m²

उत्तर :

(a) 1, (b) 3, (e) 4, (d) 4, (e) 4, (f) 4.

प्रश्न 11:

धातु की किसी आयताकार शीट की लम्बाई, चौड़ाई व मोटाई क्रमशः 4,234 m, 1.005 m व 2.01 cm है। उचित सार्थक अंकों तक इस शीट का पृष्ठीय क्षेत्रफल व आयतन ज्ञात कीजिए।

उत्तर :

यहाँ लम्बाई 4 = 4.234 m, चौड़ाई b =1.005 m

तथा मोटाई c = 2.01 cm = 0.0201 m

स्पष्ट है कि लम्बाई व चौड़ाई में 4-4 सार्थक अंक हैं जबकि मोटाई में 3 सार्थक अंक हैं।

∴ पृष्ठीय क्षेत्रफल तथा आयतन दोनों का अधिकतम 3 सार्थक अंकों में पूर्णांकन करना होगा।

अब शीट का पृष्ठीय क्षेत्रफल

= 2x (ab + bc + ca)
= 2x [4.234 x 1.005 + 1.005 x 0.0201 + 0.0201 x 4234] m²
= 2x [4.25517 + 0.0202005 + 0.0851034] m²
= 2 x 4.3604739 m = 8.7209478 m = 8.72 m²
जबकि शीट का आयतन = ल० x चौ० x ऊँ०
= 4.234 m x 1.005 m x 0.0201 m
= 0.085528917 m³
= 0.0855 m³

प्रश्न 12:

पंसारी की तुला द्वारा मापे गए डिब्बे का द्रव्यमान 2.300 kg है। सोने के दो टुकड़े जिनका द्रव्यमान क्रमशः 20.15 g व 20.17 g है, डिब्बे में रखे जाते हैं

(a) डिब्बे का कुल द्रव्यमान कितना है,

(b) उचित सार्थक अंकों तक टुकड़ों के द्रव्यमानों में कितना अन्तर है?

उत्तर :

(a) दिया है : डिब्बे का द्रव्यमान = 2300 kg

पहले टुकड़े का द्रव्यमान = 20.15 g = 0.02015 kg

दूसरे टुकड़े का द्रव्यमान = 2017 g= 0.02017 kg

∴ टुकड़े रखने के बाद डिब्बे का कुल द्रव्यमान

= 2.300 kg + 0.02015 kg + 0.02017kg

= 2.34032 kg

∵ तीनों मांपों में डिब्बे के द्रव्यमान में सबसे कम सार्थक अंक (4 अंक) हैं; अतः डिब्बे के कुल द्रव्यमान का अधिकतम चार सार्थक अंकों में पूर्णांकन करना होगा।

∴ डिब्बे का कुल द्रव्यमान = 2.340 kg

(b)∵ सोने के टुकड़ों के द्रव्यमानों में प्रत्येक में 4 सार्थक अंक हैं; अतः इनके अन्तर का अधिकतम

दशमलव के दूसरे स्थान तक पूर्णांकन करना होगा।

टुकड़ों के द्रव्यमानों का अन्तर = 20.17 g – 20.16 g= 0.02 g

प्रश्न 13:

कोई भौतिक राशि P, चार प्रेक्षण-योग्य राशियों a, b,c तथा d से इस प्रकार

a, b, c तथा d के मापने में प्रतिशत त्रुटियाँ क्रमशः 1%, 3%, 4% तथा 2% हैं। राशि P में प्रतिशत त्रुटि कितनी है? यदि उपर्युक्त सम्बन्ध का उपयोग करके P का परिकलित मान 3. 763 आता है तो आप परिणाम का किस मान तक निकटन करेंगे?

उत्तर :

P के मान में त्रुटि 0.489 से स्पष्ट है कि P के मान में दशमलव के पहले स्थान पर स्थित अंक ही संदिग्ध है; अत: P के मान को दशमलव के दूसरे स्थान तक लिखना व्यर्थ है। अतः P के मान का. दशमलव के पहले स्थान तक पूर्णांकन करना होगा।

अतः P का निकटतम मान = 3.763 = 3.8

प्रश्न 14:

किसी पुस्तक में, जिसमें छपाई की अनेक त्रुटियाँ हैं, आवर्त गति कर रहे किसी कण के विस्थापन के चार भिन्न सूत्र दिए गए हैं

(a = कण का अधिकतम विस्थापन, ν = कण की चाल, T = गति का आवर्तकाल)।

विमीय आधारों पर गलत सूत्रों को निकाल दीजिए।

उत्तर :

किसी त्रिकोणमितीय फलन का कोण एक विमाहीन राशि होती है।

सूत्र (b) तथा (c) में कोण vt तथा ! विमाहीन नहीं हैं; अत: उपर्युक्त दोनों सूत्र सही नहीं हैं। शेष दोनों सूत्र (a) तथा (d) सही हैं।

प्रश्न 15:

भौतिकी का एक प्रसिद्ध सम्बन्ध किसी कण के चल द्रव्यमान (moving mass) m,  विराम द्रव्यमान (rest mass) m0, इसकी चाल ν और प्रकाश c की चाल  के बीच है। (यह सम्बन्ध सबसे पहले अल्बर्ट आइन्स्टाइन के विशेष आपेक्षिकता के सिद्धान्त के परिणामस्वरूप उत्पन्न हुआ था।) कोई छात्र इस सम्बन्ध को लगभग सही याद करता है। लेकिन स्थिरांक c को लगाना भूल जाता है। वह लिखता है

अनुमान लगाइए कि c कहाँ लगेगा?

उत्तर :

दिया गया सम्बन्ध है।

प्रश्न 16:

परमाण्विक पैमाने पर लम्बाई का सुविधाजनक मात्रक ऍग्स्ट्रॉम है और इसे (1 = 10^-10m) द्वारा निर्दिष्ट किया जाता है। हाइड्रोजन के परमाणु का आमाप लगभग 0.5 A है। हाइड्रोजन परमाणुओं के एक मोल का m’ में कुल आण्विक आयतन कितना होगा?

उत्तर :

प्रश्न 17:

किसी आदर्श गैस का एक मोल (ग्राम अणुक) मानक ताप व दाब पर 22.4L आयतन (ग्राम अणुक आयतन) घेरता है। हाइड्रोजन के ग्राम अणुक आयतन तथा उसके एक मोल के परमाण्विक आयतन का अनुपात क्या है? (हाइड्रोजन के (की आमाप लगभग 1मानिए)। यह अनुपात इतनी अधिक क्यों है?

उत्तर :

एक मोल हाइड्रोजन गैस का आयतन = 22.4

L =22.4 x 10^-3 m³

जबकि 1 मोल हाइड्रोजन गैस का परमाण्विक आयतन=3.15 x 10^-7 m³ (प्रश्न 16 के परिणाम से)

इसे अनुपात का मान इतना अधिक होने का अर्थ है कि गैस का आयतन उसमें उपस्थित अणुओं के वास्तविक आयतन की तुलना में बहुत अधिक होता है। इसका अन्य अर्थ यह है कि गैस के अणुओं के बीच बहुत अधिक खाली स्थान होता है।

प्रश्न 18:

इस सामान्य प्रेक्षण की स्पष्ट व्याख्या कीजिए : यदि आप तीव्र गति से गतिमान किसी रेलगाड़ी की खिड़की से बाहर देखें तो समीप के पेड़, मकान आदि रेलगाड़ी की गति की विपरीत दिशा में तेजी से गति करते प्रतीत होते हैं, परन्तु दूरस्थ पिण्ड (पहाड़ियाँ, चन्द्रमा, तारे आदि) स्थिर प्रतीत होते हैं। (वास्तव में क्योंकि आपको ज्ञात है कि आप चल रहे हैं, इसलिए ये दूरस्थ वस्तुएँ आपको अपने साथ चलती हुई प्रतीत होती हैं।)

उत्तर :

किसी वस्तु का हमारे सापेक्ष गति करते हुए प्रतीत होना, हमारे सापेक्ष वस्तु के कोणीय वेग पर निर्भर करता है न कि उसके रेखीय वेग पर। यद्यपि गाड़ी से यात्रा करते समय सभी वस्तुएँ समान वेग से हमारे पीछे की ओर गति करती हैं, परन्तु समीप स्थित वस्तुओं का हमारे सापेक्ष कोणीय वेग अधिक होता है; अतः वे तेजी से पीछे जाती प्रतीत होती हैं जबकि दूर स्थित वस्तुओं का हमारे सापेक्ष कोणीय वेग बहुत ही कम होता है; अतः वे हमें लगभग स्थिर प्रतीत होती हैं।

प्रश्न 19:

समीपी तारों की दूरियाँ ज्ञात करने के लिए लम्बन के सिद्धान्त का प्रयोग किया जाता है। सूर्य के परितः अपनी कक्षा में छः महीनों के अन्तराल पर पृथ्वी की अपनी, दो स्थानों को मिलाने वाली, आधार रेखा AB है। अर्थात आधार रेखा पृथ्वी की कक्षा के व्यास≈ 3x 1011 m के लगभग बराबर है। लेकिन चूंकि निकटतम तारे भी इतने अधिक दूर हैं। कि इतनी लम्बी आधार रेखा होने पर भी वे चाप के केवल 1″ (सेकण्ड, चाप का) की कोटि का लम्बन प्रदर्शित करते हैं। खगोलीय पैमाने पर लम्बाई का सुविधाजनक मात्रक पारसेक है। यह किसी पिण्ड की वह दूरी है जो पृथ्वी से सूर्य तक की दूरी के बराबर आधार रेखा के दो विपरीत किनारों से चाप के 1′ का लम्बन प्रदर्शित करती है। मीटरों में एक पारसेक कितना होता है?

उत्तर :

प्रश्न 20:

हमारे सौर परिवार से निकटतम तारा 4.29 प्रकाश वर्ष दूर है। पारसेक में यह दूरी कितनी है? यह तारा (ऐल्फा सेटौरी नामक) तब कितना लम्बन प्रदर्शित करेगा जब इसे सूर्य के परितः अपनी कक्षा में पृथ्वी के दो स्थानों से जो छः महीने के अन्तराल पर हैं, देखा, जाएगा?

उत्तर :

प्रश्न 21:

भौतिक राशियों का परिशुद्ध मापन विज्ञान की आवश्यकताएँ हैं। उदाहरण के लिए, किसी शत्रु के लड़ाकू जहाज की चाल सुनिश्चित करने के लिए बहुत ही छोटे समयान्तरालों पर इसकी स्थिति का पता लगाने की कोई यथार्थ विधि होनी चाहिए। द्वितीय विश्वयुद्ध में रेडार की खोज के पीछे वास्तविक प्रयोजन यही था। आधुनिक विज्ञानं के उन भिन्न उदाहरणों को सोचिए जिनमें लम्बाई, समय, द्रव्यमान आदि के परिशुद्ध मापन की आवश्यकता होती है। अन्य जिस किसी विषय में भी आप बता सकते हैं, परिशुद्धता की मात्रात्मक धारणा दीजिए।

उत्तर :

लम्बाई का मापन: विभिन्न यौगिकों के क्रिस्टलों में परमाणुओं के बीच की दूरी का मापन करते समय लम्बाई के परिशुद्ध मापन की आवश्यकता होती है।।

समय का मापन: फोको की विधि द्वारा किसी माध्यम में प्रकाश की चाल ज्ञात करने के प्रयोग में समय के परिशुद्ध मापन की आवश्यकता होती है।

द्रव्यमान का मापन: द्रव्यमान स्पेक्ट्रमलेखी में परमाणुओं के द्रव्यमान का परिशुद्ध मापन किया जाता है।

प्रश्न 22:

जिस प्रकार विज्ञान में परिशुद्ध मापन आवश्यक है, उसी प्रकार अल्पविकसित विचारों तथा सामान्य प्रेक्षणों को उपयोग करने वाली राशियों के स्थूल आकलन कर सकना भी उतना ही महत्त्वपूर्ण है। उन उपायों को सोचिए जिनके द्वारा आप निम्नलिखित का अनुमान लगा सकते हैं-(जहाँ अनुमान लगाना कठिन है वहाँ राशि की उपरिसीमा पता लगाने का प्रयास कीजिए)

(a) मानसून की अवधि में भारत के ऊपर वर्षाधारी मेघों का कुल द्रव्यमान।

(b) किसी हाथी का द्रव्यमान।।

(c) किसी तूफान की अवधि में वायु की चाल।

(d) आपके सिर के बालों की संख्या।

(e) आपकी कक्षा के कमरे में वायु के अणुओं की संख्या।

उत्तर :

(a) सर्वप्रथम मौसम विभाग से पूरे भारत में हुई कुल वर्षा की माप की जानकारी लेंगे और वर्षा जल के आयतन को जल के घनत्व से गुणा करके वर्षा जल के द्रव्यमान की गणना कर लेंगे। इससे मेघों का द्रव्यमान ज्ञात हो जाएगा।

(b) ट्रक आदि का द्रव्यमान मापने वाले काँटे पर खड़ा करके हाथी को द्रव्यमान ज्ञात किया जा सकता है।

(c) किसी तूफान की अवधि में वायु द्वारा उत्पन्न दाब को मापकर, वायु की चाल का आकलन किया जा सकता है।

(d) सिर के 1cm² क्षेत्रफल में स्थित बालों को गिन लिया जाएगा। तत्पश्चात् सिर के क्षेत्रफल का आकलन करके इस क्षेत्रफल से 1cm² क्षेत्रफल में स्थित बालों की संख्या को गुणा करके सिर के बालों की संख्या का आकलन किया जा सकता है।

(e) कक्षा के कमरे में उपस्थित वायु का घनत्व नापकर 1cm3 आयतन में उपस्थित अणुओं की संख्या की गणना की जा सकती है। तत्पश्चात् कमरे के आयतन से गुणा करके कक्षा के कमरे में उपस्थित वायु के अणुओं की गणना की जा सकती है।

प्रश्न 23:

सूर्य एक ऊष्म प्लैज्मा (आयनीकृत पदार्थ) है जिसके आन्तरिक क्रोड का ताप 10⁷K से अधिक और बाह्य पृष्ठ का ताप लगभग 6000 K है। इतने अधिक ताप पर कोई भी पदार्थ ठोस या तरल प्रावस्था में नहीं रह सकता। आपको सूर्य का द्रव्यमान घनत्व किस परिसर में होने की आशा है? क्या यह ठोसों, तरलों या गैसों के घनत्वों के परिसर में है? क्या आपका अनुमान सही है, इसकी जाँच आप निम्नलिखित आँकड़ों के आधार पर कर सकते हैं- सूर्य का द्रव्यमान = 2.0×10³⁰ kg सूर्य की त्रिज्या = 7.0 x 10⁸ m.

उत्तर :

प्रश्न 24:

जब बृहस्पति ग्रह पृथ्वी से 8247 लाख किलोमीटर दूर होता है तो इसके व्यास की कोणीय माप 35.72′ का चाप है। बृहस्पति का व्यास परिकलित कीजिए।

उत्तर :

दिया है, बृहस्पति ग्रह की पृथ्वी से दूरी

s= 8247 लाख किलोमीटर = 8247 x 10⁵ किमी

अतिरिक्त अभ्यास

प्रश्न 25:

वर्षा के समय में कोई व्यक्ति चाल) के साथ तेजी से चला जा रहा है। उसे अपने छाते को टेढ़ा करके ऊर्ध्व के साथ 8 कोण बनाना पड़ता है। कोई विद्यार्थी कोण 8 व 9 के बीच निम्नलिखित सम्बन्ध व्युत्पन्न करता है-tan θ = ν

और वह इस सम्बन्ध के औचित्य की सीमा पता लगाता है: जैसी कि आशा की जाती है। यदि v→0 तो θ →0(हम यह मान रहे हैं कि तेज हवा नहीं चल रही है और किसी खड़े व्यक्ति के लिए वर्षा ऊध्वधरतः पड़ रही है)। क्या आप सोचते हैं कि यह सम्बन्ध सही हो सकता है? यदि ऐसा नहीं है तो सही सम्बन्ध का अनुमान लगाइए।

उत्तर :

दिए गए सम्बन्ध में,

∵ दोनों पक्षों की विमाएँ परस्पर समान नहीं हैं; अत: यह सम्बन्ध सही नहीं हो सकता। स्पष्ट है कि सही सम्बन्ध में दाएँ पक्ष की विमाएँ भी [L⁰] होनी चाहिए। माना वर्षा की बूंदें u वेग से ऊर्ध्वाधरत: नीचे गिर रही हैं, तब दाएँ पक्ष को विमाहीन करने के लिए ν को u से भाग देना चाहिए।

प्रश्न 26:

यह दावा किया जाता है कि यदि बिना किसी बाधा के 100 वर्षों तक दो सीजियम घड़ियों को चलने दिया जाए तो उनके समयों में केवल 0.02 s का अन्तर हो सकता है। मानक सीजियम घड़ी द्वारा 1s के समय अन्तराल को मापने में यथार्थता के लिए इसका क्या अभिप्राय है?

उत्तर :

कुल समय = 100 वर्ष, T = 100 x 365 x 24 x 60 x 60 s

100 वर्ष के अन्तराल में त्रुटि ∆T = 0.02s

प्रश्न 27:

एक सोडियम परमाणु का आमाप लगभग 2.5  मानते हुए उसके माध्य द्रव्यमान घनत्व का अनुमान लगाइए। (सोडियम के परमाणवीय द्रव्यमान तथा आवोगाद्रो संख्या के ज्ञात मान का प्रयोग कीजिए)। इस घनत्व की क्रिस्टलीय प्रावस्था में सोडियम के घनत्व 970 kg m-3 के साथ तुलना कीजिए। क्या इन दोनों घनत्वों के परिमाण की कोटि समान है? यदि हाँ, तो क्यों?

उत्तर :

सोडियम परमाणु का आमाप (त्रिज्या) = 2.5 = 2.5 x 10^-10 m

सोडियम का ग्राम परमाणु भार = 23 g= 23 x 10^-3 kg

एक ग्राम परमाणु में परमाणुओं की संख्या 6.023 x  10²³ होती है।

स्पष्ट है कि परमाणु का द्रव्यमान घनत्व तथा ठोस प्रावस्था में सोडियम का घनत्व दोनों 103 की कोटि के हैं। इसका अर्थ यह है कि ठोस प्रावस्था में परमाणुओं के बीच खाली स्थान नगण्य होता है, अर्थात् ठोस प्रावस्था में परमाणु दृढ़तापूर्वक संकुलित होते हैं।

प्रश्न 28:

नाभिकीय पैमाने पर लम्बाई का सुविधाजनक मात्रक फर्मी है-(1f=10^-15 m)। नाभिकीय आमाप लगभग निम्नलिखित आनुभविक सम्बन्ध का पालन करते हैं  r =r₀ A^1/3 जहाँ नाभिक की त्रिज्या,A इसकी द्रव्यमान संख्या और r₀ कोई स्थिरांक है जो लगभग 1.2 f के बराबर है। यह प्रदर्शित कीजिए कि इस नियम का अर्थ है कि विभिन्न नाभिकों के लिए नाभिकीय द्रव्यमान घनत्व लगभग स्थिर है। सोडियम नाभिक के द्रव्यमान घनत्व का आकलन कीजिए। प्रश्न 27 में ज्ञात किए गए सोडियम परमाणु के माध्य द्रव्यमान घनत्व के साथ इसकी तुलना कीजिए।

उत्तर :

माना किसी नाभिक की द्रव्यमान संख्या A है तथा प्रत्येक न्यूक्लिऑन (न्यूट्रॉन तथा प्रोटॉन) का द्रव्यमान m0 (नियतांक) है।

अर्थात् सोडियम नाभिक का घनत्व उसके परमाणु के घनत्व से लगभग 1015 गुना अधिक है। इसका अर्थ यह है कि परमाणु का अधिकांश भाग खोखला है तथा उसका अधिकांश द्रव्यमान उसके नाभिक में निहित है।

प्रश्न 29:

लेसर (LASER), प्रकाश के अत्यधिक तीव्र, एकवर्णी तथा एकदिश किरण-पुंज का स्रोत है। लेसर के इन गुणों का लम्बी दूरियाँ मापने में उपयोग किया जाता है। लेसर को प्रकाश के स्रोत के रूप में उपयोग करते हुए पहले ही चन्द्रमा की पृथ्वी से दूरी परिशुद्धता के साथ ज्ञात की जा चुकी है। कोई लेसर प्रकाश किरण-पुंज चन्द्रमा के पृष्ठ से परावर्तित होकर 2.56 s में वापस आ जाता है। पृथ्वी के परितः चन्द्रमा की कक्षा की त्रिज्या कितनी है?

उत्तर :

प्रश्न 30:

जल के नीचे वस्तुओं को ढूंढने व उनके स्थान का पता लगाने के लिए सोनार (SONAR) में पराश्रव्य तरंगों का प्रयोग होता है। कोई पनडुब्बी सोनार से सुसज्जित है। इसके द्वारा जनित अन्वेषी तरंग और शत्रु की पनडुब्बी से परावर्तित इसकी प्रतिध्वनि की प्राप्ति के बीच काल विलम्ब 77.0 s है। शत्रु की पनडुब्बी कितनी दूर है? (जल में ध्वनि की चाल = 1450 m s^-1)

उत्तर :

प्रश्न 31:

हमारे विश्व में आधुनिक खगोलविदों द्वारा खोजे गए सर्वाधिक दूरस्थ पिण्ड इतनी दूर हैं। कि उनके द्वारा उत्सर्जित प्रकाश को पृथ्वी तक पहुँचने में अरबों वर्ष लगते हैं। इन पिण्डों (जिन्हें क्वासर Quasar’ कहा जाता है) के कई रहस्यमय लक्षण हैं जिनकी अभी तक सन्तोषजनक व्याख्या नहीं की जा सकी है। किसी ऐसे क्वासर की km में दूरी ज्ञात कीजिए जिससे उत्सर्जित प्रकाश को हम तक पहुँचने में 300 करोड़ वर्ष लगते हों।

उत्तर :

प्रश्न 32:

यह एक विख्यात तथ्य है कि पूर्ण सूर्यग्रहण की अवधि में चन्द्रमा की चक्रिका सूर्य की चक्रिका को पूरी तरह ढक लेती है। चन्द्रमा का लगभग व्यास ज्ञात कीजिए।

(पृथ्वी से चन्द्रमा की दूरी = 3.84 x 10⁸ m सूर्य का कोणीय व्यास = 1920′ )

उत्तर :

माना कि चन्द्रमा का कोणीय व्यास = d

जबकि चन्द्रमा की पृथ्वी से दूरी = 3.84 x 10⁸ m

प्रश्न 33:

इस शताब्दी के एक महान भौतिकविद् (पी०ए०एम० डिरैक) प्रकृति के मूल स्थिरांकों (नियतांकों) के आंकिक मानों के साथ क्रीड़ा में आनन्द लेते थे। इससे उन्होंने एक बहुत ही रोचक प्रेक्षण किया। परमाणवीय भौतिकी के मूल नियतांकों (जैसे इलेक्ट्रॉन का द्रव्यमान, प्रोटॉन का द्रव्यमान तथा गुरुत्वीय नियतांक G) से उन्हें पता लगा कि वे एक ऐसी संख्या पर पहुँच गए हैं जिसकी विमा समय की विमा है। साथ ही, यह एक बहुत ही बड़ी संख्या थी और इसका परिमाण विश्व की वर्तमान आकलित आयु (~1500 करोड़ वर्ष) के करीब है। इस पुस्तक में दी गई मूल नियतांकों की सारणी के आधार पर यह देखने का प्रयास कीजिए कि क्या आप भी यह संख्या (या और कोई अन्य रोचक संख्या जिसे आप सोच सकते हैं) बना, सकते हैं? यदि विश्व की आयु तथा इस संख्या में समानता महत्त्वपूर्ण है तो मूल नियतांकों की स्थिरता किस प्रकार प्रभावित होगी?

उत्तर :

परीक्षोपयोगी प्रश्नोत्तर

बहुविकल्पीय प्रश्न

प्रश्न 1:

निम्नलिखित में से कौन-सा S.I. मात्रक नहीं है?

(i) ऐम्पियर

(ii) केण्डिला

(iii) न्यूटन

(iv) केल्विन

उत्तर :

(iii) न्यूटन

प्रश्न 2:

निम्नलिखित में से कौन दूरी का मात्रक नहीं है?

(i) ऐंग्स्ट्रॉम

(ii) फर्मी

(iii) बार्न

(iv) पारसेक

उत्तर :

(iii) बार्न

प्रश्न 3.

पारसेक मात्रक है।

(i) समय का

(ii) दूरी को

(iii) आवृत्ति का

(iv) कोणीय संवेग का

उत्तर :

(ii) दूरी का

प्रश्न 4.

प्रकाश वर्ष मात्रक है।

(i) समय का

(ii) दूरी का

(iii) वेग का

(iv) प्रकाश की तीव्रता का

उत्तर :

(ii) दूरी का

प्रश्न 5:

नाभिकीय त्रिज्या 10^-15 मीटर कोटि की है। इसे व्यक्त करने के लिए उपयुक्त मात्रक है

(i) माइक्रोन

(ii) मिमी

(iii) ऐंग्स्ट्राम

(iv) फर्मी

उत्तर :

(iv) फर्मी

प्रश्न 6:

निम्नलिखित में से व्युत्पन्न मात्रक है।

(i) केण्डिला

(ii) किग्रा

(iii) न्यूटन

(iv) मीटर

उत्तर :

(iii) न्यूटन

प्रश्न 7:

1 मीटर तुल्य है।

(i) 10¹⁰ 
(ii) 10⁸ 
(iii) 10⁶ 
(iv) 10⁵ 

उत्तर :

(i) 10¹⁰ 

प्रश्न 8.

एक माइक्रोन (μ) होता है।

(i) 10^-9 मी
(ii) 10^-12 मी
(iii) 10^-6 मी
(iv) 10^-15 मी

उत्तर :

(iv) 10^-15 मी

प्रश्न 9:

एक नैनोमीटर तुल्य है ।

(i) 10^-9 मिमी
(ii) 10^-6 सेमी
(iii) 10^-7 सेमी
(iv) 10^-9 सेमी

उत्तर :

(iii) 10^-7 सेमी

प्रश्न 10:

1 सेकण्ड तुल्य है।

(i) क्रिप्टॉन घड़ी के 1650763.73 आवर्गों के

(ii) क्रिप्टॉन घड़ी के 652189.63 आवर्ती के

(iii) सीजियम घड़ी के 1650763.73 आवर्ती के

(iv) सीजियम घड़ी के 91926317770 आवर्ती के

उत्तर :

(iv) सीजियम घड़ी के 91926317770 आवर्ती के

प्रश्न 11:

1 मीटर में Kr86 की कितनी तरंगदैर्ध्य होती है?

(i) 1553164.13

(ii) 1650763.73

(iii) 2348123.73

(iv) 652189.63

उत्तर :

(ii) 1650763.73

प्रश्न 12:

एक प्रकाश वर्ष दूरी बराबर है।

(i) 9.46 x 10¹⁰ किमी
(ii) 9.46 x 10¹² किमी
(iii) 9.46 x 10¹² मीटर
(iv) 9.46 x 10¹⁵ सेमी

उत्तर :

(ii) 9.46 x 10¹² किमी

प्रश्न 13:

106 डाइन/सेमी2 का दाब किसके बराबर है?

10⁶ डाइन/सेमी² का दाब किसके बराबर है?
(i) 10⁷ न्यूटन/मीटर²
(ii) 10⁶ न्यूटन/मीटर²
(iii) 10⁵ न्यूटन/मीटर²
(iv) 10⁴ न्यूटन/मीटर²

उत्तर :

(iii) 10°न्यूटन/मीटर2,

अतिलघु उत्तरीय प्रश्न

प्रश्न 1:

किसी भौतिक राशि के मापन से क्या तात्पर्य है?

उत्तर :

किसी भौतिक राशि की इसके मात्रक से तुलना करना ही मापन कहलाता है।

प्रश्न 2:

किसी राशि की माप को पूर्णतया व्यक्त करने के लिए किन-किन बातों का ज्ञान होना आवश्यक है?

उत्तर :

किसी राशि की माप को पूर्णतया व्यक्त करने के लिए निम्नलिखित बातों का ज्ञान होना आवश्यक है

1.  मात्रक: जिसमें वह भौतिक राशि मापी जाती है।
2.  आंकिक मान: यह उस राशि के परिमाण को प्रदर्शित करता है अर्थात् यह बताता है कि उस राशि की माप में उसका मात्रक कितनी बार सम्मिलित है।

प्रश्न 3:

मात्रक कितने प्रकार के होते हैं?

उत्तर :

मात्रक दो प्रकार के होते हैं-

(i) मूल मात्रक,

(ii) व्युत्पन्न मात्रक।

प्रश्न 4:

S.I. प्रणाली क्या है?

उत्तर :

सात मूल मात्रकों तथा दो पूरक मूल मात्रकों पर आधारित माप की प्रणाली S.I. प्रणाली कहलाती है।।

प्रश्न 5:

MKS प्रणाली के मूल मात्रकों के नाम लिखिए।

उत्तर :

MKS प्रणाली के मूल मात्रक मीटर, किग्रा, सेकण्डे, ऐम्पियर, केण्डिला तथा केल्विन होते हैं।

प्रश्न 6:

शेक किस भौतिक राशि का मात्रक है?

उत्तर :

यह समय का मात्रक है तथा 1 शेक = 10^-8 सेकण्ड।

प्रश्न 7:

नाभिक के आकार को व्यक्त करने के लिए कौन-सा मात्रक प्रयुक्त किया जाता है? इसका मीटर से क्या सम्बन्ध है?

उत्तर :

फर्मी, जहाँ 1 फर्मी (F) = 10^-15 मीटर।

प्रश्न 8:

चन्द्रशेखर सीमा किस यौगिक राशि का मात्रक है?

उत्तर :

यह द्रव्यमान का मात्रक है तथा 1 CS.L.= 1.4 x सूर्य का द्रव्यमान।।

प्रश्न 9:

AU  तथा  क्या हैं? इनमें पारस्परिक सम्बन्ध क्या हैं?

उत्तर :

AU  तथा  लम्बाई के ही भिन्न-भिन्न मात्रक हैं। AU लम्बाई का खगोलीय मात्रक है तथा A लम्बाई की छोटा मात्रक है।।

1 AU =1.496 x 10²¹ 

प्रश्न 10:

स्लग (Slug) क्या है? 1 स्लग में मीट्रिक टनों की संख्या कितनी होगी?

उत्तर :

स्लग (Slug) बड़े द्रव्यमान मापने का एक मात्रक है।

तथा 1 स्लग = 14.59 किग्रा

∵ 1 मीट्रिक टन = 1000 किग्रा

∴ 1 स्लग =14.32

= 1459 x 10^-3  मीट्रिक टन

प्रश्न 11:

क्या प्रकाश वर्ष समय का मात्रक है?

उत्तर :

नहीं, प्रकाश वर्ष दूरी का मात्रक है।

प्रश्न 12:

माइक्रोसेकण्ड तथा शेक में क्या सम्बन्ध है?

उत्तर :

प्रश्न 13:

प्रकाश वर्ष को परिभाषित कीजिए।

उत्तर :

1 प्रकाश वर्ष वह दूरी है जो प्रकाश निर्वात् में 1 वर्ष में तय करता है।

∴ 1 प्रकाश वर्ष = 9.46 x 10¹⁵ मीटर
या निर्वात् में 1 प्रकाश वर्ष = 9.46 x 10¹³ मीटर

प्रश्न 14:

1 सेकण्ड माध्य-सौर-दिवस का कौन-सा भाग होता है?

उत्तर :

1 सेकण्ड माध्य-सौर-दिवस का 86,400वाँ भाग होता है।

प्रश्न 15:

एक मीटर में कितने प्रकाश-वर्ष होते हैं?

उत्तर :

हम जानते हैं कि,

प्रश्न 16:

पृथ्वी से प्रेषित एक लेसर पुंज चन्द्रमा से परावर्तन के पश्चात पृथ्वी पर 2.6 सेकण्ड बाद वापस लौटता है। पृथ्वी से चन्द्रमा की दूरी ज्ञात कीजिए।

उत्तर :

यहाँ, समय t = 2.6 सेकण्ड,

लेसर पुंज का वेग c = 3x 10⁸ मी/से

लघु उत्तरीय प्रश्न

प्रश्न 1:

मूल मात्रक क्या हैं? इनके चार गुण लिखिए।

उत्तर :

मूल राशियों के वे मात्रक जो एक-दूसरे से पूर्णतया स्वतन्त्र होते हैं तथा इनमें से किसी एक मात्रक को किसी अन्य मात्रक से बदला अथवा उससे सम्बन्धित नहीं किया जा सकता है, मूल मात्रक कहलाते हैं। लम्बाई, द्रव्यमान, समय, वैद्युतधारा, ऊष्मागतिक ताप, ज्योति तीव्रता तथा पदार्थ की मात्रा मूल मात्रक हैं। मूल. मात्रकों के गुण निम्नलिखित हैं

1.  यह बाह्य कारकों से अप्रभावित रहना चाहिए।
2.  यह सुपरिभाषित होना चाहिए।
3.  इसे सरलतापूर्वक निर्मित किया जाना चाहिए।
4.  इसका उपयोग सरल होना चाहिए।

प्रश्न 2:

व्युत्पन्न मात्रक किसे कहते हैं? किसी एक भौतिक राशि का व्युत्पन्नमात्रक प्राप्त कीजिए।

उत्तर :

मूल राशियों के अतिरिक्त अन्य सभी भौतिक राशियों के मात्रक एक अथवा अधिक मूल मात्रकों पर उपयुक्त घातें लगाकर प्राप्त किये जा सकते हैं। ऐसे मात्रकों को व्युत्पन्न मात्रक (derived units) कहते हैं। बल का व्युत्पन्न मात्रक निम्न प्रकार से प्राप्त कर सकते हैं

बलु = द्रव्यमान x त्वरण

बल का मात्रक = किग्रा x मीटर/सेकण्ड^-2

= किग्रा-मीटर सेकण्ड^-2

परन्तु S.I. प्रणाली में बल का व्यावहारिक मात्रक न्यूटन होता है।

∴ 1 न्यूटन = 1 किग्रा-मीटर सेकण्ड^-2

प्रश्न 3:

गुरुत्वीय द्रव्यमान और जड़त्वीय द्रव्यमान में अन्तर स्पष्ट कीजिए।

उत्तर :

किसी वस्तु पर कार्यरतु पृथ्वी के गुरुत्वाकर्षण बल तथा पृथ्वी की ओर मुक्त रूप से गिरती वस्तु के गुरुत्वीय जनित त्वरण का अनुपात, वस्तु का गुरुत्वीय द्रव्यमान कहलाता हैं, जबकि किसी वस्तु पर लगाए गए कुल बाह्य बल तथा उसके कारण वस्तु में उत्फन त्वरण का अनुपात वस्तु का जड़त्वीय द्रव्यमान कहलाता है।

प्रश्न 4:

मापन की यथार्थता तथा परिशुद्धता में अन्तर स्पष्ट कीजिए।

उत्तर :

1.  किसी मापन की यथार्थता वह मान है जो हमें यह बताती है कि किसी राशि का मापित मान उसके वास्तविक मान के कितना निकट है, जबकि किसी मापन की परिशुद्धता यह बताती है कि वह राशि किस सीमा या विभेदन तक मापी गई है।
2. किसी भी मापक यन्त्र की यथार्थती उस यन्त्र में विद्यमान उसकी क्रमबद्ध त्रुटि पर निर्भर करती है, जबकि किसी भी मापक यन्त्र की परिशुद्धता यादृच्छिक त्रुटियों पर निर्भर करती है।

प्रश्न 5:

किसी राशि के परिमाण की कोटि से क्या तात्पर्य है? उदाहरण सहित समझाइये।

उत्तर :

यदि किसी राशि के परिमाण को उसके निकटतम 10 की पूर्णाक घात के रूप में लिखा जाए, तो प्राप्त परिमाण को इस राशि को कोटिमान (कोटि) कहते हैं।

उदाहरण:

किसी राशि 0.0025 = 2.5 x 10^-3 में 2.5, 3.16 से छोटा है, तो इस राशि का कोटिमान 10^-3 होगा, जबकि एक अन्य राशि 0.0035 = 3.5 x 10^-3 में 3.5, 3.16 से बड़ा है, तो इस राशि का कोटिमान 10^-3+1 = 10^-2 होगा।

प्रश्न 6:

पृथ्वी के व्यास के दो विपरीत छोरों से किसी आकाशीय पिण्ड का विस्थापनाभास (parallax) 60 सेकण्ड है। यदि पृथ्वी की त्रिज्या 64 x 10⁶ मीटर हो, तो पृथ्वी के केन्द्र से आकाशीय पिण्ड की दूरी ज्ञात कीजिए। इस दूरी को खगोलीय मात्रक में परिवर्तित कीजिए। (1 A.U.= 1.5 x 10¹¹ मीटर)

उत्तर :

विस्तृत उत्तरीय प्रश्न

प्रश्न 1:

लम्बन तथा लम्बनकोण से क्या तात्पर्य है? पृथ्वी के निकट स्थित तारे की दूरी ज्ञात करने के लिए लम्बन विधि का वर्णन कीजिए।

उत्तर :

लम्बन तथा लम्बनकोण-जब हम किसी दीवार पर अंकित किसी चिह्न P को पहले अपनी बायीं आँख A(दायीं आँख B बन्द रखते हुए) देखते हैं और फिर उसी बिन्दु को अपनी दायीं आँख B से (बायीं आँख A बन्द रखते हुए) देखते हैं तो दीवार के सापेक्ष चिह्न की स्थिति में आभासी विस्थापन दिखायी देता है। इस आभासी विस्थापन को ही लम्बन कहते हैं दूरी AB को आधार दूरी कहते हैं।

AP तथा BP के बीच का कोण θ लम्बनकोण कहलाता है।

पृथ्वी के निकट स्थित तारे की दूरी ज्ञात करना—दिए गए चित्र 2.3 में सूर्य S के परितः पृथ्वी की परिक्रमण कक्षा का व्यास AB है। N एक तारा है जो पृथ्वी के निकट स्थित है तथा इस तारे N की ही पृथ्वी से दूरी ज्ञात करनी है। चित्र 2.3 में F एक अन्य तारा है जो पृथ्वी से काफी दूरी पर स्थित है। माना किसी क्षण पृथ्वी की अपनी कक्षा में स्थिति A है। खगोलीय दूरदर्शी द्वारा ∠FAN = θ, ज्ञात कर । लिया जाता है। में ∠ANS =∠ FAN = θ.6 माह के समयान्तराल पर पृथ्वी अपनी कक्षा में स्थिति A के ठीक सामने स्थिति B में होगी। अब खगोलीय दूरदर्शी द्वारा ∠NBF = 8ज्ञात कर लिया जाता है।

∠BNS =∠ NBF = θ,

तथा ∠ANB=∠ANS + ∠BNS

= θ1 + θ2.

यह कोण तारे N द्वारा पृथ्वी के व्यास AB पर शीर्षाभिमुख बनने वाला कोण है।

प्रश्न 2:

आवोगाने विधि द्वारा परमाणु के आकार का आकलन किस प्रकार किया जा सकता है? समझाइए।

उत्तर :

आवोगाद्रो के अनुसार, पदार्थ के एक ग्राम-परमाणु में 6023 x 10²³ परमाणु होते हैं, जो पदार्थ का लगभग दो-तिहाई आयतेन घेरते हैं। माना पदार्थ का द्रव्यमान m, पदार्थ का परमाणु भार M, पदार्थ द्वारा घेरा गया आयतन V, परमाणु की त्रिज्या तथा आवोगाद्रो संख्या N है। तब,

चूंकि आयतन V, परमाणु भार M, आवोगाद्रो संख्या N तथा पदार्थ का द्रव्यमान m ज्ञात हैं, अतः परमाणु की त्रिज्या । नापी जा सकती है, जिसका मान लगभग 10-10 मीटर की कोटि का होता है।

एनसीईआरटी सोलूशन्स क्लास 11 भौतिक विज्ञान पीडीएफ

• 1. भौतिक जगत
• 3. सरल रेखा में गति
• 4. समतल में गति
• 5. गति के नियम
• 6. कार्य, ऊर्जा तथा शक्ति
• 7. कणों के नियम तथा घूर्णी गति
• 8. गुरुत्वाकर्षण
• 9. ठोसों के यांत्रिक गुण
• 10. तरलों के यांत्रिक गुण
• 11. द्रव्य के तापीय गुण
• 12. ऊष्मागतिकी
• 13. अणुगति सिद्धांत
• 14. दोलन
• 15. तरंगें