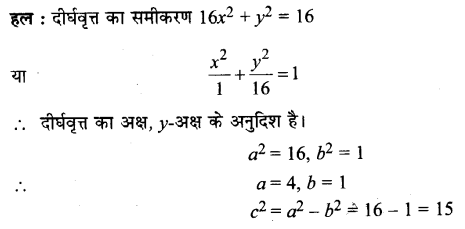NCERT Solutions Class 11 गणित-II Chapter-11 (शंकु परिच्छेद)
Class 11 गणित-II
पाठ-11 (शंकु परिच्छेद)
अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर
निम्नलिखित प्रश्न 1 से 5 तक प्रत्येक में वृत्त का समीकरण ज्ञात कीजिए:
प्रश्न 1.
केंद्र (0, 2) और त्रिज्या 2 इकाई।
हल:
यहाँ h = 0, k = 2 तथा r = 2 रखने पर,
वृत्त का समीकरण, (x – 0)² + (y – 2)² = 2²
x² + y² – 4y + 4 = 4
अतः वृत्त का अभीष्ट समीकरण, x² + y² – 4y = 0.
प्रश्न 2.
केंद्र (-2, 3) और त्रिज्या 4 इकाई।
हल:
वृत्त का समीकरण (x + 2)² + (y – 3)² = 4²
या (x²+ 4x + 4) + (y² – 6y + 9) = 16
या x² + y² + 4x – 6y – 3 = 0.
प्रश्न 3.
केंद्र (,
) और त्रिज्या
इकाई।
प्रश्न 4.
केंद्र (1, 1) और त्रिज्या √2 इकाई।
हल:
यहाँ h = 1, k = 1 तथा r = √2 हों, तब
वृत्ते का समीकरण,
(x – 1)² + (y – 1)² = (√2)²
(x² – 2x + 1) + (y² – 2y + 1) = 2
x² + y² – 2x – 2y = 0.
प्रश्न 5.
केंद्र (-a, -b) और त्रिज्या √(a² – b²) इकाई।
हल:
वृत्त का समीकरण,
(x + a)² + (y + b)² = {√(a² – b²)}²
x² + 2ax + a² + y² + 2by + b² = a² – b²
x² + y² + 2ax + 2by + 2b² = 0.
निम्नलिखित प्रश्न 6 से 9 तक में प्रत्येक वृत्त का केन्द्र और त्रिज्या ज्ञात कीजिए:
प्रश्न 6.
(x + 5)² + (y – 3)² = 36.
हल:
वृत्त (x + 5)² + (y – 3)² = 36 की (x – h)² + (y – k)² = r² से तुलना करने पर,
– h = 5, -k = – 3, r² = 36
h = -5, k = 3, r = 6
केन्द्र (-5, 3), त्रिज्या = 6.
प्रश्न 7.
x² + y² – 4x – 8y – 45 = 0
प्रश्न 8.
x² + y² – 8x + 10y – 12 = 0.
हल:
(x² – 8x) + (y² + 10y) = 12
या (x² – 8x + 16) + (y² + 10y + 25) = 12 + 16 + 25
(x – 4)² + (y + 5)² = 53
केन्द्र (4, -5), त्रिज्या = √53.
प्रश्न 9.
2x² + 2y² – x = 0.
प्रश्न 10.
बिन्दुओं (4, 1) और (6, 5) से जाने वाले वृत्त का समीकरण ज्ञात कीजिए जिसका केन्द्र रेखा 4x + y = 16 पर स्थित है।
हल:
वृत्त का व्यापक समीकरण
x² + y² + 2gx + 2fy + c = 0
बिन्दु (4, 1) इस पर स्थित है।
16 + 1 + 8g + 2f + c = 0
8g + 2f + c = – 17 ……(1)
बिन्दु (6, 5) वृत्त पर स्थित है।
36 + 25 + 12g + 10f + c = 0
12g + 10f + c = -61 ……..(2)
केंद्र (-g, -f) रेखा 4x + y = 16 पर स्थित है।
-4g – f = 16.
4g + f = -16 ………(3)
समीकरण (1) को (2) में से घटाने पर
4g + 8f = -44
समीकरण (3) को (4) में से घटाने पर
7f = -44 + 16 = – 28
f = -4
समीकरण (3) में का मान रखने पर
4g – 4 = -16 या 4g = -12
g = -3
f और g का मान समी (1) में रखने पर
– 24 – 8 + c = – 17
c = 32 – 17 = 15
अत: वृत्त का समीकरण
x² + y² – 6x – 8y + 15 = 0.
प्रश्न 11.
बिन्दुओं (2, 3) और (-1, 1) से जाने वाले वृत्त का समीकरण ज्ञात कीजिए जिसका केंद्र रेखा x – 3y – 11 = 0 पर स्थित है।
हल:
मान लीजिए वृत्त का समीकरण x² + y² + 2gx + 2fy + c = 0 …..(1)
इस पर बिन्दु (2, 3) स्थित है।
4 + 9 + 4g + 6f + c = 0
4g + 6f + c = -13 …..(2)
इसी प्रकार (-1, 1) भी वृत्त (1) पर स्थित है।
1 + 1 – 2g + 2 + c = 0
-2g + 2f + c = -2 …….(3)
केंद्र (-g, -f) रेखा x – 3y – 11 = 0 पर स्थित है।
-g + 3f – 11 = 0
या -g + 3f = 11 ……(4)
समीकरण (2) में से (3) को घटाने पर
6g + 4f = -11 ……..(5)
समी. (4) को 6 से गुणा करने पर,
– 6g + 18f = 66 ……(6)
समी. (5) और समी (6) को जोड़ने पर,
22f = 55
⇒ f = \frac { 5 }{ 2 }
f का मान समी (5) में रखने पर,
6g + 10 = -11
6g = -21
g = \frac { -7 }{ 2 }
g और f का मान समी (3) में रखने पर,
7 + 5 + c = -2 या c = – 14
g, और c के मान समीकरण (1) में रखने पर,
x² + y² – 7x + 5y – 14 = 0
यह वृत्त का वांछित समीकरण है।
प्रश्न 12.
त्रिज्या 5 के उस वृत्त का समीकरण ज्ञात कीजिए जिसका केंद x-अक्ष पर हो और जो बिन्दु (2, 3) से जाता है।
हल:
केंद्र x-अक्ष पर है। मान लीजिए ऐसा बिन्दु (p, 0) है। त्रिज्या 5 वाले वृत्त का समीकरण
(x – p)² + (y – 0)² = 25
बिन्दु (2, 3) इस वृत्त से होकर जाता है।
(2 – p)² + 9 = 25
(2 – p)² = 25 – 9 = 16
2 – p = ±4
+ve चिन्ह लेने पर, 2 – p = 4 या p = 2 – 4 = -2
-ve चिन्ह लेने पर, 2 – p = -4 या 2 = 4 + 2 = 6
जब p = -2, वृत्त का समीकरण
(x + 2)² + y = 25
x² + y² + 4x – 21 = 0
जब p = 6, वृत्त का समीकरण
(x – 6)² + y² = 25
x² + y² – 12x + 36 – 25 = 0
x² + y² – 12x + 11 = 0
वृत्त के अभीष्ट समीकरण
x² + y² + 4x – 21 = 0 और x² + y² – 12x + 11 = 0
प्रश्न 13.
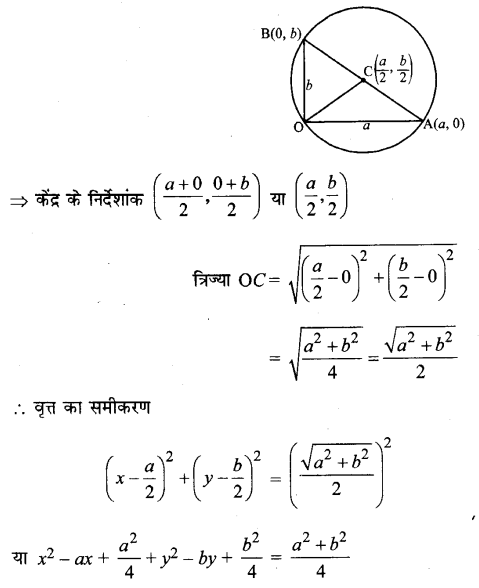
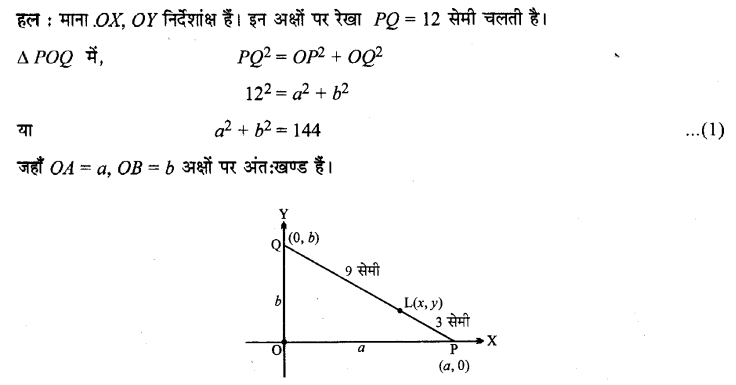
(0, 0) से होकर जाने वाले वृत्त का समीकरण ज्ञात कीजिए जो निर्देशांक्षों पर a और B अंतः खण्ड बनाता है।
हल:
वृत्त मूल बिन्दु से होकर जाता है और अक्षों पर अंत:खण्ड a, b बनाता है।
OA = a, A के निर्देशांक (a, 0)
OB = b, B के निर्देशांक (0, b)
प्रश्न 14.
उस वृत्त का समीकरण ज्ञात कीजिए जिसका केंद्र (2, 2) हो तथा (4, 5) से जाता है।
प्रश्न 15.
क्या बिन्दु (-2.5, 3.5) वृत्त x² + y² = 25 के अंदर, बाहर या वृत्त पर स्थित है।
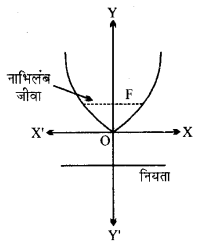
निम्नलिखित प्रश्न 1 से 6 तक प्रत्येक में नाभि के निर्देशांक, परवलय का अक्ष, नियता का समीकरण और नाभिलंब जीवा की लंबाई ज्ञात कीजिए।
प्रश्न 1.
y² = 12x
हल:
परवलय का समीकरण, y² = 12x
y² = 4ax से तुलना करने पर।
4a = 12 या a = 3
(i) नाभि के निर्देशांक (a, 0) या (3, 0)
(ii) परवलय का अक्ष OX
इसका समीकरण y = 0
(iii) नियता का समीकरण : x = -a अर्थात् x = -3
(iv) नाभिलंब जीवा की लंबाई = 4a = 12.
प्रश्न 2.
x² = 6y
हल:
परवलय का समीकरण x² = 6y
4a = 6 या a =
इसका अक्ष y-अक्ष है जिसका
(i) समीकरण x = 0 है।
(ii) नाभि F (0, a) के निर्देशांक (0, ) है।
(iii) नियता y = -a का समीकरण y =
(iv) नाभिलंब जीवा की लम्बाई 4a = 6.
प्रश्न 3.
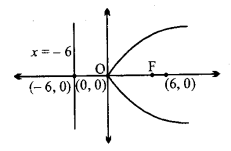
y² = -8x
हल:
परवलय का समीकरण y² = -8x
4a = 8 ⇒ a = 2
(i) नाभि F(-a, 0) के निर्देशांक (-2, 0)
(ii) परवलय का अक्ष x-अक्ष
इसका समीकरण y = 0
(iii) नियता x = a का समीकरण x = 2.
(iv) नाभिलंब जीवा की लंबाई = 4a = 8.
प्रश्न 4.
x² = -16y.
हल:
परवलय का समीकरण x² = -16y
4a = 16 या a = 4
(i) नाभि F (0, – a) के निर्देशांक (0, -4)
(ii) परवलय अक्ष का समीकरण x = 0.
(iii) नियता y = 0 का समीकरण y = 4.
(iv) नाभिलंब जीवा की लंबाई 4a = 16.
प्रश्न 5.
y² = 10x.
हल:
परवलय का समीकरण y² = 10x (आकृति प्रश्न 1 में देखें)
4a = 10 या a = \frac { 5 }{ 2 }
(i) नाभि F (a, 0) के निर्देशांक (\frac { 5 }{ 2 }, 0)
(ii) परवलय को अक्ष : x-अक्ष, समीकरण y = 0
(iii) नियता x = -a का समीकरण x = \frac { -5 }{ 2 }
(iv) नाभिलंब जीवा की लंबाई 4a = 10.
प्रश्न 6.
x² = -9y.
हल:
परवलय का समीकरण x² = -9y (आकृति प्रश्न 4 में देखें)।
4a = 9 या a = \frac { 9 }{ 4 }
(i) नाभि (0, -a) के निर्देशांक (0, \frac { -9 }{ 4 })
(ii) परवलय का अक्ष : y-अक्ष, समीकरण x = 0
(ii) नियता y = a का समीकरण y = \frac { 9 }{ 4 }
(iv) नाभिलंब जीवा की लंबाई 4a = 9.
निम्नलिखित प्रश्न 7 से 12 तक प्रत्येक में परवलय का समीकरण ज्ञात कीजिए जो दिए प्रतिबंध को संतुष्ट करता है।
प्रश्न 7.
नाभि (6, 0), नियता x = – 6.
हल:
परवलंय का अक्ष : x-अक्ष, y = 0
शीर्ष (0, 0) है, नाभि के निर्देशांक (6, 0)
परवलय का अक्ष, धन x-अक्ष के अनुदिश है।
परवलय का समीकरण y² = 24x.
प्रश्न 8.
नाभि (0, -3), नियता y = 3.
हल:
परवलय का अक्ष y-अक्ष है।
शीर्ष (0, -3), (0, 3) का मध्य बिन्दु (0, 0) है। नाभि (0, -3) से स्पष्ट होता है कि परवलय की अक्ष OY के अँनुदिश है।
परवलय के समीकरण का रूप x² = -4ay
यहाँ पर a = 3, 4a = 12
परवलय का समीकरण x = -12y.
प्रश्न 9.
शीर्ष (0, 0), नाभि (3, 0) (आकृति प्रश्न 7 की देखिए)
हल:
परवलय का अक्ष OX के अनुदिश हैं।
परवलय के समीकरण का रूप y = 4ax
नाभि (3, 0) है।
a = 3
4a = 4 x 3 = 12
परवलय का समीकरण y² = 12x.
प्रश्न 10.
शीर्ष (0, 0), नाभि (-2, 0).
हल:
परवलय का अक्ष OX’ के अनुदिश
नाभि (-2, 0) है तो a = 2
4a = 8
परवलय का रूप y² = -4ax
परवलय का समीकरण y² = – 8x.
प्रश्न 11.
शीर्ष (0, 0), (2, 3) से जाता है और अक्ष, x-अक्ष के अनुदिश है।
हल:
परवलय का शीर्ष (0, 0) है और अक्ष : x-अक्ष है।
परवलय के समीकरण का रूप y² = 4ax
यह बिन्दु (2, 3) से होकर जाता है।
9 = 4a x 2
या 4a =
अतः परवलय का समीकरण y² = x या 2y² = 9x.
प्रश्न 12.
शीर्ष (0, 0), (5, 2) से जाता है और y-अक्ष के सापेक्ष सममित है।
हल:
शीर्ष (0, 0), परवलय y-अक्ष के सापेक्ष सममित है।
समीकरण का रूप x² = 4ay है।
यह बिन्दु (5, 2) से गुजरता है।
25 = 4a x 2
4a =
परवलय का समीकरण, x² = y या 2x² = 25y.
निम्नलिखित प्रश्नों 1 से 9 तक प्रत्येक दीर्घवृत्त में नाभियों और शीर्षों के निर्देशांक, दीर्घ और लघु अक्ष की लंबाइयाँ, उत्केंदता तथा नाभिलंबे जीवा की लम्बाई ज्ञात कीजिए।
प्रश्न 7.
36x² + 4y² = 144.
प्रश्न 8.
16x² + y² = 16.
प्रश्न 9.
4x² + 9y² = 36.
निम्नलिखित प्रश्नों 10 से 20 तक प्रत्येक में, दिए प्रतिबंधों को संतुष्ट करते हुए दीर्घवृत्त का समीकरण ज्ञात कीजिए।
प्रश्न 10.
शीर्षों (±5, 0), नाभियाँ (±4, 0).
हल:
a = 5, c = 4, c² = a² – b².
प्रश्न 11.
शीर्षों (0, ±13), नाभियाँ (0, ±5).
प्रश्न 12.
शीर्ष (±6, 0), नाभियाँ (±4, 0)
प्रश्न 13.
दीर्घ अक्ष के अंत्य बिन्दु (±3, 0), लघु अक्ष के अंत्य बिन्दु (0, ±2).
प्रश्न 14.
दीर्घ अक्ष के अंत्य बिन्दु (0, ±√5), लघु अक्ष के अंत्य बिन्दु (±1, 0).
हल:
दीर्घ अक्ष, y-अक्ष के अनुदिश है।
a = √5, b = 1,
a² = 5, b² = 1.
प्रश्न 15.
दीर्घ अक्ष की लंबाई = 26, नाभियाँ (±5, 0).
प्रश्न 16.
दीर्घ अक्ष की लंबाई = 16, नाभियाँ (0, ±6).
प्रश्न 17.
नाभियाँ (±3, 0), a = 4.
प्रश्न 18.
b = 3, c = 4, केन्द्र मूल बिन्दु पर, नाभियाँ x-अक्ष पर है।
प्रश्न 19.
केंद्र (0, 0) पर, दीर्घ अक्ष y-अक्ष पर और बिन्दुओं (3, 2) और (1, 6) से जाता है।
प्रश्न 20.
दीर्घ अक्ष, x-अक्ष पर और बिन्दुओं (4, 3), (6, 2) से जाता है।
निम्नलिखित प्रश्न 1 से 6 तक प्रत्येक में, अतिपरवलयों के शीर्षों, नाभियों के निर्देशांक, उत्केंद्रता और नाभिलंब जीवा की लंबाई ज्ञात कीजिए।
प्रश्न 3.
9y² – 4x² = 36.
प्रश्न 4.
16x² – 9y² = 576.
प्रश्न 5.
5y² – 9x² = 36.
प्रश्न 6.
49y² – 16x² = 784.
निम्नलिखित प्रश्न 7 से 15 तक प्रत्येक में, दिए गए प्रतिबंधों को संतुष्ट करते हुए अतिपरवलयका समीकरण ज्ञात कीजिए।
प्रश्न 7.
शीर्ष (±2, 0), नाभियाँ (±3, 0).
प्रश्न 8.
शीर्ष (0, ±5), नाभियाँ (0, ±8).
प्रश्न 9.
शीर्ष (0, ±3), नाभियाँ (0, ±5).
प्रश्न 10.
नाभियाँ (±5, 0), अनुप्रस्थ अक्ष की लम्बाई = 8.
हल:
अनुप्रस्थ अक्ष की लम्बाई = 2a = 8
a = 4
a² = 16
प्रश्न 11.
नाभियाँ (0, ±13), संयुग्मी अक्ष की लम्बाई = 24.
प्रश्न 12.
नाभियाँ (±3√5, 0), नाभिलंब जीवा की लम्बाई = 8.
प्रश्न 13.
नाभियाँ (±4, 0), नाभिलंब जीवा की लम्बाई 12 है।
प्रश्न 14.
शीर्ष (±7, 0), e =
प्रश्न 15.
नाभियाँ (0, ±√10) हैं तथा (2, 3) से होकर जाता है।
अध्याय 11 पर विविध प्रश्नावली
प्रश्न 1.
यदि एक परवलयाकार परावर्तक का व्यास 20 सेमी और गहराई 5 सेमी है, तो नाभि ज्ञात कीजिए।
हल:
परवलयाकार परावर्तक AOB का व्यास,
AB = 20 सेमी
AM = 10 सेमी
परावर्तक की गहराई, OM = 5 सेमी
यदि OX, OY निर्देशांक अक्ष हो तो बिन्दु परवलय पर स्थित है।
माना परवलय का समीकरण, y² = 4ax
10² = 4a x 5 या 100 = 20a या a = 5
परवलय की नाभि (a, 0) या (5, 0) है।
प्रश्न 2.
एक मेहराब परवलय के आकार का है और इसका अक्ष ऊर्ध्वाधर है। मेहराब 10 मीटर ऊँचा है और आधार में 5 मीटर चौड़ा है। यह परवलय के दो मीटर की दूरी पर शीर्ष से कितना चौड़ा होगा?
हल:
इसका आकार परवलय की आकृति का है।
माना OX, OY इसके निर्देशांक अक्ष है, और समीकरण y² = 4ax है।
मेहराब की ऊँचाई, OL = 10 मीटर
चौड़ाई EF = 5 मीटर
LF =
EF = x 5 =
प्रश्न 3.
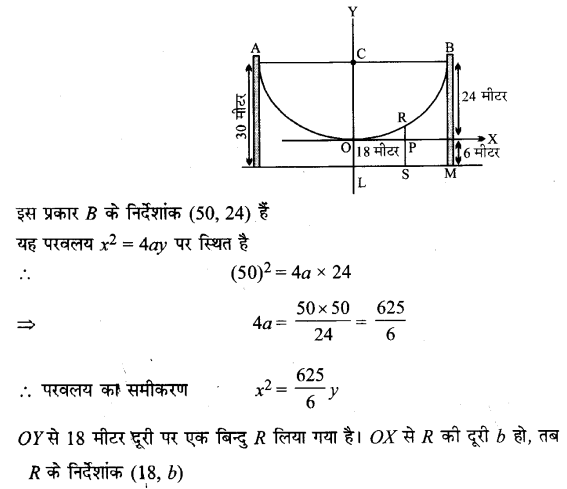
एक सर्वसम भारी झूलते पुल की केबिल (cable) परवलय के रूप में लटकी हुई है। सड़क पथ जो क्षैतिज है 100 मीटर लम्बा है तथा केबिल से जुड़े अर्ध्वाधर तारों पर टिका हुआ है, जिसमें सबसे लम्बा तार 30 मीटर और सबसे छोटा तार 6 मीटर है। मध्य से 18 मीटर दूर सड़क पथ से जुड़े समर्थक (supporting) तार की लंबाई ज्ञात कीजिए।
हल:
माना OX, OY निर्देशांक अक्ष हैं। AOB परवलय के रूप में केबिल है। इसका समीकरण x² = 4ay के रूप में होगा।
सबसे छोटे तार की लम्बाई OL = 6 मीटर
सबसे बड़े तार की लम्बाई BM = 30 मीटर
शीर्ष O से रेखा LM की दूरी OL = 6 मीटर है।
सड़क की लंबाई AB = 100 मीटर, यदि C मध्य बिन्दु हो तो
CB = AB =
x 100 = 50 मीटर
OC = CL – OL = 30 – 6 = 24 मीटर
प्रश्न 4.
एक मेहराब अर्ध-दीर्घवृत्ताकार रूप का है। यह 8 मीटर चौड़ा है और केंद्र से 2 मीटर ऊँचा है। एक. सिरे से 1.5 मीटर दूर बिन्दु पर मेहराब की ऊँचाई ज्ञात कीजिए।
हल:
आकृति में ELF एक मेहराब है जिसकी चौड़ाई EF = 8 मीटर और ऊंचाई = 2 मीटर है।
माना OX, OY निर्देशांक अक्ष है। ELF एक दीर्घवृत्त है जिसमें a = 4, b = 2
प्रश्न 5.
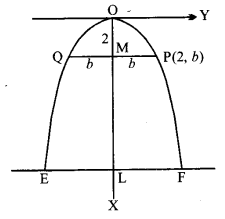
एक 12 सेमी छड़ इस प्रकार चलती है कि इसके सिरे निर्देशांक्षों को स्पर्श करते हैं। छड़ के बिन्दु P का बिन्दुपथ ज्ञात कीजिए जो x-अक्ष के संपर्क वाले सिरे से 3 सेमी दूर है।
प्रश्न 6.
त्रिभुज का क्षेत्रफल ज्ञात कीजिए जो परवलय x² = 12y के शीर्ष को इसकी नाभिलंब जीवा के सिरों को मिलाने वाली रेखाओं से बना है।
हल:
परवलय का समीकरण, x² = 12y
नाभि के निर्देशांक (a, 0) या (3, 0) हैं।
OF = 3 इकाई
नाभिलंब जीवा की लंबाई = 4a = 12
ΔPOQ का क्षेत्रफल = x OF x PQ
= x 3 x 12
= 18 वर्ग इकाई।
प्रश्न 7.
एक व्यक्ति दौड़पथ पर दौड़ते हुए अंकित करता है कि उससे दो झंडा चौकियों की दूरियों का योग सदैव 10 मीटर रहता है। और झंडा चौकियों के बीच की दूरी 8 मीटर है। व्यक्ति द्वारा बनाए पथ का समीकरण ज्ञात कीजिए।
प्रश्न 8.
परवलय y² = 4ax के अंतर्गत एक समबाहु त्रिभुज है जिसका एक शीर्ष परवलय का शीर्ष है। त्रिभुज की भुजा की लंबाई ज्ञात कीजिए।
हल:
परवलय y² = 4ax, एक समबाहु त्रिभुज बनाई गई है।
मान लीजिए इसकी भुजा की लंबाई p है।
एनसीईआरटी सोलूशन्स क्लास 11 गणित-I
- 1. सम्मुच्य
- 2. संबंध एवं फलन
- 3. त्रिकोणमितीय फलन
- 4. गणितीय आगमन का सिद्धांत
- 5. सम्मिश्र संख्याएँ और द्विघातीय समीकरण
- 6. रैखिक असमिकाएँ
- 7. क्रमचय एवं संचय
- 8. द्विपद प्रमेय
- 9. अनुक्रम तथा श्रेणी