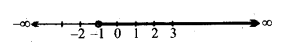NCERT Solutions Class 11 गणित-I Chapter-6 (रैखिक असमिकाएँ)
Class 11 गणित-I
पाठ-6 (रैखिक असमिकाएँ)
अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर
Exercise 6.1
प्रश्न 1.
हल कीजिए : 24x < 100, जब
(i) x एक प्राकृत संख्या है।
(ii) x एक पूर्णांक है। 24x < 100
हल:
24x < 100
24 से दोनों पक्षों में भाग करने पर
x < अर्थात x <
(i) यदि x एक प्राकृत संख्या है तो हल {1, 2, 3, 4} है।
(ii) यदि x एक पूर्णांक संख्या है तो हल {…. -3, -2, -1, 0, 1, 2, 3, 4}.
प्रश्न 2.
हल कीजिए: 12x > 30, जब
(i) x एक प्राकृत संख्या है।
(ii) x एक पूर्णाक है।
हल:
– 12x > 30
-12 से दोनों पक्षों में भाग करने पर,
x < अर्थात x <
(i) यदि x प्राकृत संख्या है तो कोई हल नहीं है।
(ii) यदि x पूर्णाक संख्या है तो हल {….. -5, -4, -3} है।
प्रश्न 3.
हल कीजिए : 5x – 3 < 7, जब
(i) x एक पूर्णाक है।
(ii) x एक वास्तविक संख्या है।
हल:
5x – 3 < 7
दोनों पक्षों में 3 जोड़ने पर,
5x < 10
5 से भाग देने पर
x <
अर्थात x < 2
(i) यदि x एक पूर्णांक संख्या है तो हल {…. -2, -1, 0, 1}.
(ii) यदि x एक वास्तविक संख्या है तो हल x ∈ (-∞, 2).
प्रश्न 4.
हल कीजिए : 3x + 8 > 2, जब
(i) x एक पूर्णाक है।
(ii) एक वास्तविक संख्या है।
हल:
3x + 8 > 2
3x > 2 – 8 या 3x > -6 .
3 से भाग करने पर
x > या x > -2
(i) यदि x एक पूर्णांक संख्या है तो हल {-1, 0, 1, 2,….}.
(ii) यदि x एक वास्तविक संख्या है तो हल x ∈ (-2, ∞).
प्रश्न 5.
हल कीजिए : 4x + 3 < 6x + 7.
हल:
4x + 3 < 6x + 7
6x को बाएँ पक्ष में तथा 3 को दाएँ पक्ष में रखने पर,
4x – 6x < 7 – 3,
-2x < 4 -2 से भाग देने पर, x > या x > -2
दी हुई असमिका का हल है: x = (-2, ∞).
प्रश्न 6.
हल कीजिए : 3x – 7 > 5x – 1
हल:
3x -7 > 5x – 1
5x को बाएँ पक्ष में और 7 को दाएँ पक्ष में रखने पर,
3x – 5x > -1 + 7
या
-2x > 6
-2x से भाग देने पर।
x < -3
दी हुई असमिका का हल है x ∈ (-∞, – 3).
प्रश्न 7.
हल कीजिए : 3(x – 1) ≤ 2 (x – 3).
हल:
असमिका
3(x – 1) ≤ 2 (x – 3)
3x – 3 ≤ 2x – 6
2x को बाएँ पक्ष में और 3 को दाएँ पक्ष में रखने पर,
3x – 2 ≤ 3 – 6
x < – 3
हल है : x ∈ (-∞, – 3].
प्रश्न 8.
हल कीजिए : 3 (2 – x) ≥ 2 (1 – x).
हल:
दी हुई असमिका 3(2 – x) ≥ 2 (1 – x)
6 – 3x ≥ 2 – 2x
2x को बायीं ओर तथा 6 को दायीं ओर रखने पर,
2x – 3x ≥ 2 – 6
या
-x ≥ -4 या x ≤ 4
हल है : x ∈ (-∞, 4]
प्रश्न 13.
हल कीजिए : 2 (2x + 3) – 10 < 6 (x – 2)
हल:
दी हुई असमिका 2 (2x + 3) – 10 < 6 (x – 2)
4x + 6 – 10 < 6x – 12
6x को बायीं ओर तथा -4 को दार्थी ओर रखने पर,
4 – 6x < -12 + 4
-2x < -8 (-1) से गुणा करने पर, x > 4
हल है :
x ∈ (4, ∞)
प्रश्न 14.
हल कीजिए : 37 – (3x + 5) ≥ 9x – 8(x – 3).
हल:
दी हुई असमिका 37 – (3x + 5) ≥ 9x – 8(x – 3)
37 – 3x – 5 ≥ 9x – 8x + 24
– 3x + 32 ≥ x + 24
x को बायीं ओर तथा 32 को दायीं ओर रखने पर
-3x – x ≥ 24 – 32
– 4x ≥ – 8
(-1) से गुणा करने पर तथा 4 से भाग देने पर।
x ≤ या x ≤ 2
हल है: x ∈ (-∞, 2].
प्रश्न 17 से 20 तक की असमिकाओं को हल ज्ञात कीजिए तथा उन्हें संख्या रेखा पर आलेञ्चित कीजिए।
प्रश्न 17.
3x – 2 < 2x + 1
हल:
दी हुई असमिका . 3x – 2 < 2x + 1
2x को बायीं ओर तथा 2 को दायीं ओर रखने पर,
3x – 2x < 1 + 2
x < 3
हल है : x ∈ (-∞, 3).
प्रश्न 18.
5x – 3 ≥ 3x – 5.
हल:
दी हुई असमिका
5x -3 ≥ 3x – 5
3x को बायीं ओर तथा 3 को दायीं ओर रखने पर,
5x – 3x ≥ -5 + 3
2x ≥ -2
2 से भाग देने पर
x ≥ -1
हल है x ∈ [-1, ∞).
प्रश्न 19.
3 (1 – x) < 2 (x + 4).
हल:
दी हुई असमिका
3(1 – x) < 2(x + 4)
3 – 3x < 2x + 8
2x को बायीं ओर तथा 3 को दार्थी ओर रखने पर,
-3x – 2x < 8 – 3
– 5x < 5 -5 से भाग देने पर x > -1
हल है: x ∈ (-1, ∞)
प्रश्न 21.
रवि ने पहली दो एकक परीक्षा में 70 और 75 अंक प्राप्त किए हैं। वह न्यूनतम अंक ज्ञात कीजिए, जिसे वह तीसरी एकक परीक्षा में पाकर 60 अंक का न्यूनतम औसत प्राप्त कर सके।
हल:
मान लीजिए तीसरे एकक परीक्षा में x अंक प्राप्त किए।
प्रश्न 22.
किसी पाठ्यक्रम में ग्रेड A पाने के लिए एक व्यक्ति को सभी पाँच परीक्षाओं (प्रत्येक 100 अंकों में से) में 90 अंक या अधिक अंक का औसत प्राप्त करना चाहिए यदि सुनीता के प्रथम चार परीक्षाओं के प्राप्तांक 87, 92, 94 और 95 हों तो वह न्यूनतम अंक ज्ञात कीजिए जिसे पांचवीं परीक्षा में प्राप्त करके सुनीता उस पाठ्यक्रम में ग्रेड A पाएगी।
प्रश्न 23.
10 से कम क्रमागत विषम संख्याओं के ऐसे युग्म ज्ञात कीजिए जिनके योगफल 11 से अधिक हों।
हल:
मान लीजिए x और x + 2 दो विषम परिमेय संख्याएँ हैं।
x तथा x + 2 दोनों ही 10 से कम हैं।
⇒ x < 10 और x + 2 < 10 या x < 8 दोनों का योगं 11 से अधिक है। x + (x + 2) > 11
2x + 2 > 11 या 2x > 11 – 2
2x > 9 या x > या x > 4
अर्थात् यदि x = 5 हो, तब दूसरी संख्या = x + 2 = 7
इसी प्रकार यदि x = 7, तो x + 2 = 9
दूसरा युग्म (7, 9)
x = 9 नहीं हो सकता क्योंकि x + 2 = 11 > 10
अत: वांछित युग्म है (5, 7), 7, 9).
प्रश्न 24.
क्रमागत सर्म संख्याओं के ऐसे युग्म ज्ञात कीजिए जिनमें से प्रत्येक 5 से बड़े हों, तथा उनका योगफल 23 से कम हो।
हल:
मान लीजिए x और x + 2 दो सम संख्याएँ हैं।
x और x + 2 दोनों ही 5 से बड़ी है।
⇒ x > 5
x + (x + 2) < 23
2x + 2 < 23
2x < 23 – 2 = 21
2x < 21 या x <
यदि x = 10, x + 2 = 12 ⇒ x + (x + 2) < 23
इसी प्रकार (6, 8), (8, 10) युग्म भी दी हुई शर्त पूरी करते हैं। वांछित युग्म (6, 8), (8, 10), (10, 12).
प्रश्न 25.
एक त्रिभुज की सबसे बड़ी भुजा सबसे छोटी भुजा की तीन गुनी है तथा त्रिभुज की तीसरी भुजा सबसे बड़ी भुजा से 2 सेमी कम है। तीसरी भुजा की न्यूनतम लंबाई ज्ञात कीजिए जबकि त्रिभुज का परिमाप न्यूनतम 61 सेमी है।
हल:
मान लीजिए त्रिभुज की सबसे छोटी भुजा = x सेमी
सबसे बड़ी भुजा = 3x सेमी
तीसरी भुजा = 3x – 2 सेमी
प्रश्नानुसार
x + 3x + (3x – 2) ≥ 61
7x – 2 ≥ 61
7x ≥ 61 + 2 = 63
x ≥ 9
सबसे छोटी भुजा 9 सेमी है।
प्रश्न 26.
एक व्यक्ति 91 सेमी लंबे बोर्ड में से तीन लंबाईयाँ काटना चाहता है। दूसरी लंबाई सबसे छोटी लंबाई से 3 सेमी अधिक और तीसरी लंबाई सबसे छोटी लंबाई की दूनी है। सबसे छोटे बोर्ड की संभावित लंबाई क्या है, यदि तीसरा टुकड़ा दूसरे टुकड़े से कम से कम 5 सेमी अधिक लंबा हो ?
हल:
मान लीजिए कटे हुए सबसे छोटे बोर्ड की लंबाई = x सेमी
दूसरे कटे हुए बोर्ड की लम्बाई = x + 3
तीसरे कटे हुए बोर्ड की लम्बाई = 2x सेमी
दिया है कि
x + (x + 3) + 2x ≤ 91
4x + 3 ≤ 91
4x ≤ 91 – 3 = 88
4x ≤ 88
x ≤ 22 ……(1)
यह भी दिया गया है कि 2x ≥ (x + 3) + 5
2x ≥ x + 8
x ≥ 8 ……(2)
सबसे छोटे बोर्ड की लम्बाई कम से कम 8 सेमी हो और अधिक से अधिक 22 सेमी हो।
Exercise 6.2
निम्नलिखित असमिकाओं को आलेखन विधि से द्विविमीय तल में निरूपित कीजिए। (प्रश्न 1 से 10 तक)
प्रश्न 1.
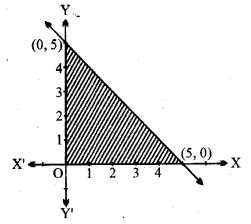
x + y < 5.
हल:
समीकरण x + y = 5 को लीजिए। यह एक सरल रेखा है जो बिन्दु (5, 0), (0, 5) से होकर गुजरती है।
x = 0, y = 0 असमिका x + y < 5 में रखने पर,
अर्थात
0 + 0 < 5 या 0 < 5
⇒ मूल बिन्दु x + y < 5 के क्षेत्र में है।
छायाकिंत क्षेत्र x + y < 5 को निरूपित करता है जो इसका हल है।
प्रश्न 2.
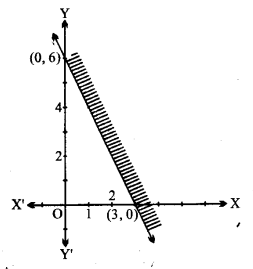
2x + y ≥ 6
हल:
2x + y ≥ 6
समीकरण 2x + y = 6 को लीजिए, यह रेखा (3, 0) और (0, 6) से गुजरती है।
x = 0, y = 0 को 2x + y ≥ 6 में रखें तो 0 ≥ 6, जो सत्य नहीं है।
मूल बिन्दु 2x + y ≥ 6 के क्षेत्र में नहीं हैं।
2x + y ≥ 6 का क्षेत्र छायांकित किया गया है।
प्रश्न 3.
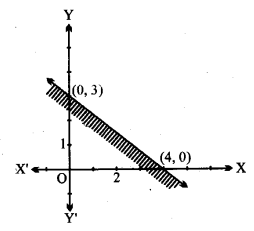
3x + 4y ≤ 12.
हल:
दी गई असमिका 3x + 4y ≤ 12 सरल रेखा 3x + 4y = 12 बिन्दु (4, 0), (0, 3) से होकर जाती है।
असमिका 3x + 4y ≤ 12 में (0, 0) रखने पर,
0 + 0 ≤ 12 अर्थात 0 ≤ 12 जो सत्य है।
मूल बिन्दु 3x + 4y ≤ 12 के क्षेत्र में आता है।
इसका आलेख साथ वाली आकृति में दिखा गया है।
प्रश्न 4.
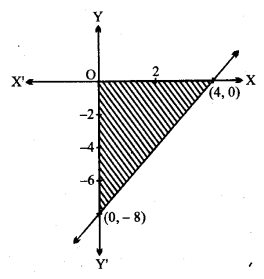
y + 8 ≥ 2x
हल:
दी हुई रैखिक असमिका y + 8 ≥ 2x सरल रेखा 2x – y = 8 बिन्दु (4, 0) और (0, -8) से होकर जाती है।
असमिका y + 8 ≥ 2x,
x = 0, y = 0 रखने पर
0 + 8 ≥ 0 अर्थात 8 ≥ 0 जो सत्य है।
मूल बिन्दु y + 8 ≥ 2x के क्षेत्र में आता है।
इसका आलेख साथ दी हुई आकृति में बनाया गया है।
प्रश्न 5.
x – y ≤ 2.
हल:
दी हुई असमिका x – y ≤ 2.
सरल रेखा x – y = 2 बिन्दु (2, 0), (0, -2) से होकर जाती है।
x = 0, y = 0 असमिका x – y ≤ 2 में रखने पर 0 ≤ 2 जो सत्य है।
मूल बिन्दु x – y ≤ 2 के क्षेत्र में है।
असमिका x – y ≤ 2 का आलेख साथ वाली आकृति में बनाया गया है।
प्रश्न 6.
2x – 3y > 6.
हल:
दी हुई रैखिक असमिका 2x – 3y > 6
सरल रेखा 2x – 3y = 6, (3, 0) और (0, -2) से होकर जाती है।
असमिका 2x – 3y > 6 में x = 0, y = 0 रखने पर 0 > 6 जो सत्य नहीं है।
मूल बिन्दु (0, 0) दी हुई असमिका में नहीं आता है।
इसका आलेख दी हुई आकृति में दर्शाया गया है।
प्रश्न 7.
-3x + 2y ≥ -6.
हल:
दी हुई रैखिक असमिका -3x + 2y ≥ -6 या 3x – 2y ≤ 6
सरल रेखा -3x + 2y = – 6 बिन्दु (2, 0) और (0, -3) से होकर जाती है।
-3x + 2y ≥ -6 में x = 0, y = 0 रखने पर 0 ≥ -6, जो सत्य है।
मूल बिन्दु (0, 0), 3x + 2y ≥ -6 असमिका के क्षेत्र में है।
इसका आलेख दी हुई आकृति में दर्शाया गया है।
प्रश्न 8.
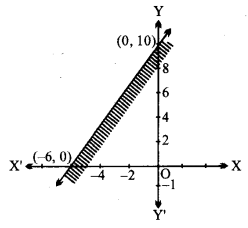
3y – 5x < 30.
हल:
दी हुई असमिका 3y – 5x < 30
सरल रेखा 3y – 5x = 30, बिन्दु (-6, 0) और (0, 10) से होकर जाती है।
असमिका 3y – 5x < 30 में x = 0, y = 0 रखने पर
0 < 30 सत्य है।
मूल बिन्दु (0, 0), 3y – 5x < 30 के क्षेत्र में है। इसका आलेख दी गई आकृति में दर्शाया गया है।
प्रश्न 9.
y < -2
हल:
दी हुई रैखिक असमिका y < -2 सरल रेखा y = -2 बिन्दु (2, -2) और (-2, -2) से होकर जाती है।
y < -2 में y = 0 रखने पर 0 < -2, यह सत्य नहीं है।
मूल बिन्दु (0, 0), < -2 में नहीं।
दी हुई आकृति में छायांकित क्षेत्र से दर्शाया गया है।
प्रश्न 10.
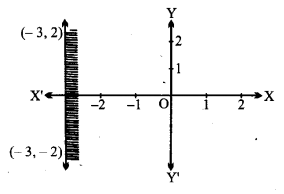
x > -3
हल:
दी हुई रैखिक असमिका x > -3
सरल रेखा x = -3 बिन्दु (-3, 2), (-3, -2) से होकर जाती है।
x > -3 में x = 0 रखने पर,
0 > -3, यह सत्य है।
मूल बिन्दु (0, 0), x > 3 में है। दी हुई आकृति में x > -3 छायांकित क्षेत्र से दर्शाया गया है।
Exercise 6.3
प्रश्न 1 से 15 तक निम्नलिखित असमिकाओं को आलेखीय विधि से हल कीजिए:
प्रश्न 1.
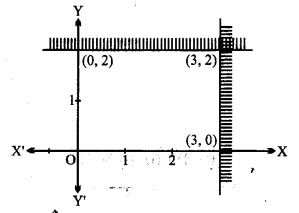
x ≥ 3, y ≥ 2
हल:
x ≥ 3, y ≥ 2
(i) सरल रेखा x = 3 बिन्दु (3, 0) और (3, 2) से होकर जाती है।
x ≥ 3 में x = 0 रखने पर 0 ≥ 3, यह सत्य नहीं है।
मूल बिन्दु (0, 0) x ≥ 3 के क्षेत्र में नहीं है।
(ii) सरल रेखा y = 2 बिन्दु (0, 2) और (3, 2) से होकर जाती है।
y ≥ 2 में y = 0 रखने पर
0 ≥ 2, यह सत्य नहीं है।
मूल बिन्दु (0, 0) इसके क्षेत्र में नहीं है।
x ≥ 3 और y ≥ 2 का हल उभयनिष्ठ छायांकित क्षेत्र से दर्शाया गया है।
प्रश्न 2.
3x + 2y ≤ 12, x ≥ 1, y ≥ 2.
हल:
दी हुई रैखिक असमिकाएँ 3x + 2y ≤ 12, x ≥ 1, y ≥ 2.
(i) रेखा 3x + 2y = 12 बिन्दु (2, 0) और (0, 6) से होकर जाती है।
3x + 2y ≤ 12 में x = 0, y = 0 रखने पर।
0 + 0 ≤ 12, अर्थात् 0 ≤ 12 जो सत्य है।
मूल बिन्दु (0, 0) इसके क्षेत्र में है।
3x + 2y ≤ 12 के हल में वे सभी बिन्दु हैं जो AB के नीचे है।
(ii) रेखा x = 1 बिन्दु B(1, 0), Q(1, 2) से होकर जाती है।
x ≥ 1 में x = 0 रखने पर
0 ≥ 1, यह सत्य नहीं है।
मूल बिन्दु इसके क्षेत्र में नहीं है।
x ≥ 1 को हल के सभी बिन्दु है जो है जो x = 1 के दाईं ओर है।
(iii) रेखा y = 2, बिन्दु C(0, 2) और D(3, 2) से होकर जाती है।
y ≥ 2 में y = 0 रखने पर 0 ≥ 2, यह सत्य नहीं है।
मूल बिन्दु (0, 0) इसके क्षेत्र में नहीं है।
y ≥ 2 का हल वे सब बिन्दु हैं जो y = 2 के ऊपर हैं।
तीनों असमिकाओं का हल इसके उभयनिष्ठ क्षेत्र ΔPOR के सभी बिन्दु हैं।
प्रश्न 3.
2x + y ≥ 6, 3x + 4y ≤ 12.
हल:
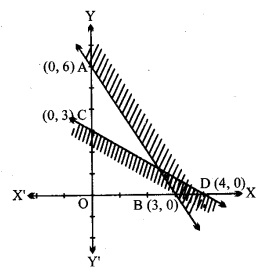
दी हुई असमिकाएँ 2x + y ≥ 6, 3x + 4y ≤ 12
(i) सरल रेखा 2x + y = 6 बिन्दु (3, 0) तथा (0, 6) से होकर जाती है।
2x + y ≥ 6 में x = 0, y = 0 रखने पर 0 ≤ 6 जो सत्य नहीं है।
मूल बिन्दु (0, 0) इसके क्षेत्र में नहीं है।
2x + y ≥ 6 का हुल वे सभी बिन्दु हैं जो 2x + y = 6 के ऊपर हैं।
(ii) सरल रेखा 3x + 4y = 12 बिन्दु D(4, 0) और C(0, 3) से होकर जाती है।
3x + 4y ≤ 12 में x = 0, y = 0 रखने पर 0 + 0 ≤ 12, जो सत्य है।
मूल बिन्दु (0, 0) इसके क्षेत्र में है।
अत: 3x +4y ≤ 12 का हल वे सब बिन्दु हैं जो रेखा CD के नीचे हैं।
इस प्रकार 2x + y ≥ 6, 3x + 4y ≤ 12 का हल वह उभयनिष्ठ क्षेत्र है जो 2x + y = 6 के ऊपर और 3x + 49 = 12 के नीचे है। यह चित्र में उभयनिष्ठ क्षेत्र द्वारा दर्शाया गया है।
प्रश्न 4.
x + y > 4, 2x – y > 0.
हल:
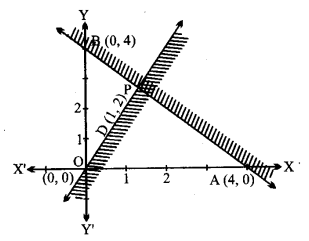
दी हुई रैखिक असमिकाएँ x + y > 4, 2x – y > 0,
(i) रेखा x + y = 4, बिन्दु (4, 0) और (0, 4) से होकर जाती है।
अब x + y > 4 में x = 0, y = 0 रखने पर, हमें प्राप्त हुआ 0 > 4 जो सत्य नहीं है।
मूल बिन्दु (0, 0) इसके क्षेत्र में नहीं है।
x + y > 4 का हल वे सब बिन्दु हैं जो रेखा AB के ऊपर है।
(ii) रेखा 2x – y = 0, बिन्दु O (0, 0) और D (1, 2) से होकर जाती है।
2x – y > 0 में x = 1, y = 0 रखते हुए 2 > 0, जो सत्य है।
बिन्दु P(1, 0), 2x – y > 0 के क्षेत्र में है।
2x – y > 0 का हल वे सब बिन्दु हैं जो OD के नीचे हैं।
प्रश्न 5.
2x – y > 1, x – 2y < -1.
हल:
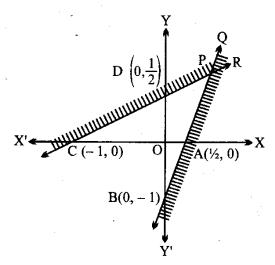
दी हुई रैखिक असमिकाएँ 2x – y > 1 और x – 2y < -1
(i) सरल रेखा 2x – y = 1 बिन्दु (\frac { 1 }{ 2 }, 0) और (0, -1) से होकर जाती है। 2x – y > 1 में x = 0, y = 0 रखने पर 0 > 1, यह सत्य नहीं है।
मूल बिन्दु (0, 0), 2x – y >1 के क्षेत्र में नहीं है।
2x – y > 1 का हल वे सब बिन्दु हैं जो रेखा AB के नीचे है।
(ii) रेखा x – 2y = -1 बिन्दु C(-1, 0) और D(0, \frac { 1 }{ 2 }) से होकर जाती है।
x – 2y < -1 में x = 0, y = 0 रखने पर 0 < -1, यह सत्य नहीं है।
मूल बिन्दु (0, 0) इसके क्षेत्र में नहीं है।
2x – y > 1 और x – 2y < -1 का हल वह उभयनिष्ठ भाग QPR है जो AB के नीचे और CD के ऊपर है।
प्रश्न 6.
x + y ≤ 6, x + y ≥ 4.
हल:
दी हुई रैखिक असमिकाएँ x + y ≤ 6 और x + y ≥ 4 है।
(i) रेखा x + y = 6, बिन्दु A(6, 0), B(0, 6) से होकर जाती है।
x + y ≤ 6 में x = 0, y= 0 रखने पर 0 + 0 ≤ 6 अर्थात् 0 ≤ 6 जो सत्य है।
मूल बिन्दु (0, 0), x + y ≤ 6 के क्षेत्र में है।
(ii) रेखा x + y = 4, बिन्दु C(4, 0) और D(0, 4) से होकर जाती है।
x + y ≥ 4 में x = 0, y = 0 रखने पर, 0 ≥ 4, यह सत्य नहीं है।
मूल बिन्दु (0, 0) x + y ≥ 4 में नहीं है। इसका हल वे सब बिन्दु हैं जो CD के ऊपर है।
दी हुई आकृति में छायांकित क्षेत्र x + y ≤ 6 और x + y ≥ 4 कै हल को दर्शाता है।
प्रश्न 7.
2x + y ≥ 8, x + 2y ≥ 10.
हल:
दी हुई रैखिक असमिकाएँ 2x + y ≥ 8, x + 2y ≥ 10.
(i) रेखा 2x + y = 8 बिन्दु A(4, 0), B(0, 8) से होकर जाती है।
2x + y ≥ 8 में x = 0, y = 0 रखने पर 0 > 8 जो असत्य है।
मूल बिन्दु (0, 0) इसके क्षेत्र में नहीं है।
2x + y ≥ 8 को हल वे सब बिन्दु हैं जो रेखा AB के ऊपर है।
(ii) रेखा x + 2y = 10, बिन्दु C(10, 0) और D(0, 5) से होकर जाती है।
x + 2y ≥ 10 में x = 0, y = 0 रखने पर,
0 ≥ 10, यह सत्य नहीं है।
मूल बिन्दु (0, 0) x + 2y ≥ 10 में नहीं है।
x + 2y ≥ 2 के सभी बिन्दु CD के ऊपर हैं।
अर्थात् 2x + y ≥ 8, x + 2y ≥ 10 का हल छायांकित उभयनिष्ठ भाग BPC है।
प्रश्न 8.
x + y ≤ 9, y > x, x ≥ 0.
हल:
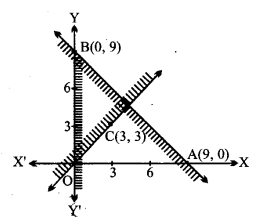
दी हुई रैखिक असमिकाएँ x + y ≤ 9, y > x, x ≥ 0
(i) सरल रेखा x + y = 9 बिन्दु A(9, 0) और B(0, 9) से होकर जाती है।
x + y ≤ 9 में x = 0, y = 0 रखते हुए 0 + 0 ≤ 9 अर्थात् 0 ≤ 9 जो सत्य है।
मूल बिन्दु (0, 0) इसके क्षेत्र में है।
x +y ≤ 9 के बिन्दु AB रेखा के नीचे हैं।
(ii) सरल रेखा y = x बिन्दु O(0, 0) और C(3, 3) से होकर जाती है।
y > x में x = 0, y = 3 रखने पर, 3 > 0 जो सत्य है।
बिन्दु (3, 0) इसके क्षेत्र में है।
y > x के सभी बिन्दु y = x के ऊपर हैं।
(iii) सरल रेखा x = 0, y-अक्ष को निरूपित करती है।
x ≥ 0 में x = 0, y = 0 रखने पर 3 ≥ 0 जो सत्य है।
x ≥ 0 के सभी बिन्दु x = 0 के दाईं ओर है।
आकृति में उभयनिष्ठ छायांकित क्षेत्र असमिकाओं x + y ≤ 9, y > x, x ≥ 0 का हल है।
प्रश्न 9.
5x + 4y ≤ 20, x ≥ 1, y ≥ 2.
हल:
दी हुई रैखिक असमिकाएँ 5x + 4y ≤ 20, x ≥ 1, y ≥ 2
सरल रेखा 5x + 4y = 20 बिन्दु A (4, 0) और B (0, 5) से होकर जाती हैं।
5x + 4y ≤ 20 में x = 0, y = 0 रखने पर, 0 + 0 ≤ 20 अर्थात् 0 ≤ 20 जो सत्य है।
मूल बिन्दु (0, 0) इसके क्षेत्र में है।
5x + 4y ≤ 20 के सभी बिन्दु रेखा AB के नीचे है।
(i) x = 1 बिन्दु C(1, 0), D(1, 2) से होकर जाती है।
x ≥ 1 में x = 0 रखने पर 0 ≥ 1 जो सत्य नहीं है।
x ≥ 1 के सभी बिन्दु x = 1 के दायीं ओर होते हैं।
(ii) y = 2, बिन्दु E(0, 2) और F(4, 2) से होकर जाती है।
y ≥ 2 में y = 0 रखने पर 0 ≥ 2 सत्य नहीं है।
मूल बिन्दु इसके क्षेत्र में नहीं है।
y ≥ 2 का हल वे सब बिन्दु हैं जो EF के ऊपर हैं।
दी हुई असमिकाओं का हल आकृति में उभयनिष्ठ PDR छायांकित क्षेत्र द्वारा दर्शाया गया है।
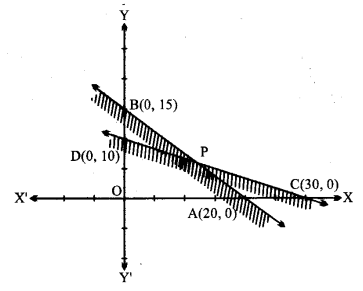
प्रश्न 10.
3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0.
हल:
दी हुई असमिकाएँ : 3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0.
(i) रेखा 3x + 4y = 60 बिन्दु A(20, 0) तथा B(0, 15) से होकर जाती है।
असमिका 3x + 4y ≤ 60 में x = 0, y = 0 रखने पर 0 ≤ 60 जो सत्य है।
मूल बिन्दु इस क्षेत्र में पड़ता है।
इस असंमिका का हल वे सब बिन्दु हैं जो AB के नीचे हैं।
(ii) रेखा x + 3y = 30 बिन्दु C(30, 0) और D(0, 10) से होकर जाती है।
असमिका x + 3y ≤ 30 में x = 0, y = 0 रखने पर 0 ≤ 30 जो सत्य है।
मूल बिन्दु इसके क्षेत्र में है।
इसका हल वे सब बिन्दु हैं जो CD के नीचे हैं।
(iii) x = 0, y-अक्ष को निरुपित करती है।
x ≥ 0 में वे सब बिन्दु हैं जो y-अक्ष की दाईं ओर हैं।
(iv) y = 0, x-अक्ष को निरुपित करती है। और y ≥ 0 में वे सब बिन्दु हैं जो x-अक्ष के ऊपर हैं।
दी हुई असमिका का हल वे सब बिन्दु हैं जो उभयनिष्ठ क्षेत्र PDOA में आते हैं।
प्रश्न 11.
2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6.
हल:
दी हुई असमिकाएँ 2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6.
(i) रेखा 2x + y = 4, बिन्दु A (2, 0) और B(0, 4) से होकर जाती है।
असमिका 2x + y ≥ 4 में x = 0, y = 0 रखने पर 0 + 0 ≥ 4 अर्थात् 0 ≥ 4जो सत्य नहीं है।
मूल बिन्दु इस क्षेत्र में नहीं है।
इसका हल वे सब बिन्दु हैं जो AB के ऊपर हैं।
(ii) रेखा x + y = 3 बिन्दु C(3, 0), D(0, 3) से होकर जाती है।
असमिका x + y ≤ 3 में x = 0, y = 0 रखने पर 0 ≤ 3 जो सत्य है। मूल बिन्दु इसके क्षेत्र में है।
इसका हल वे सब बिन्दु हैं जो CD के नीचे हैं।
(iii) रेखा 2x – 3y = 6, बिन्दु C(3, 0) और E(0, -2) से होकर जाती है।
असमिका 2x – 3y ≤ 6 में x = 0, y = 0 रखने पर 0 ≤ 6, जो सत्य है।
मूल बिन्दु इसके क्षेत्र में है। इसका हल वे सब बिन्दु हैं जो CE के ऊपर हैं।
दी हुई असमिकाओं का हल छायांकित उभयनिष्ठ क्षेत्र AQC के सब बिन्दु हैं।
प्रश्न 12.
x – 3y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1.
हल:
दी हुई असमिकाएँ x – 3y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1.
(i) रेखा x – 3y = 3 बिन्दु A(3, 0), B(0, -1) से होकर जाती है।
असमिका x – 3y ≤ 3 में x = 0, y = 0 रखने पर, 0 ≤ 3 जो सत्य है।
मूल बिन्दु इसके क्षेत्र में है। इसका हल वे सब बिन्दु हैं जो AB के ऊपर है।
(ii) रेखा 3x + 4y = 12 बिन्दु C(4, 0) और D(0, 3) से होकर जाती है।
असमिको 3x +4y ≥ 12 में x = 0, y = 0 रखने पर 0 ≥ 12, जी सत्य नहीं है। मूल बिन्दु इसके क्षेत्र में नहीं है।
इसका हल वे सब बिन्दु हैं जो CD के ऊपर है।
(iii) x = 0, y-अक्ष को दर्शाती है।
x ≥ 0 का हल वे सब बिन्दु हैं जो y-अक्ष के दाईं ओर है।
(iv) रेखा y = 1 बिन्दु E(0, 1), Q(3, 1) से होकर जाती है।
असमिका y ≥ 1 का हल वे सब बिन्दु है जो संख्या y = 1 पर पड़ते हैं या इसके ऊपर हैं।
दी हुई असमिकाओं का हल वे सब बिन्दु हैं जो उभयनिष्ठ क्षेत्र PDQRS से निरूपित किया गया है।
प्रश्न 13.
4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0.
हल:
दी हुई असमिकाएँ 4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0.
(i) सरल रेखा 4x + 3y = 60 बिन्दु A(15, 0), B(0, 20) से होकर जाती है।
4x + 3y ≤ 60 में x = 0, y = 0 रखने पर 0 ≤ 60 जो सत्य है।
मूल बिन्दु इसके क्षेत्र में है।
इस असमिका का हल वे बिन्दु हैं जो रेखा AB या AB के नीचे होते हैं।
(ii) y – 2x = 0, बिन्दु O(0, 0) और C(5, 10) से होकर जाती है।
y – 2x ≥ 0 में x = 5, y = 0 रखने पर, 0 – 10 ≥ 0 अर्थात् -10 ≥ 0 जो सत्य नहीं है।
बिन्दु (5, 0) इसके क्षेत्र में नहीं है।
y – 2x ≥ 0 को हल वे सब बिन्दु हैं जो OC पर और OC के ऊपर हैं।
(iii) रेखा x ≥ 3 बिन्दु D(3, 0), E(3, 10) से होकर जाती है।
असमिका x ≥ 3 के हल वे बिन्दु हैं जो DE या DE के दाईं ओर हैं।
(iv) x ≥ 0,y ≥ 0 पहले चतुर्थांश के बिन्दु हैं।
दी हुई असमिकाओं का हल उभयनिष्ठ क्षेत्र POR पर और उसके अन्दर के बिन्दु हैं।
प्रश्न 14.
3x + 2y ≤ 150, x + 4y ≤ 80, x ≤ 15, y ≥ 0.
हल:
दी हुई असमिकाएँ 3x + 2y ≤ 150, x + 4y ≤ 80, x ≤ 15, y ≥ 0.
(i) सरल रेखां 3x + 2y = 150, बिन्दु A(50, 0), B(0, 75) से होकर जाती है।
असमिका 3x + 2y ≤ 150 में x = 0, y = 0 रखने पर 0 ≤ 150 जो सत्य है।
मूल बिन्दु इसके क्षेत्र में है।
इसका हल वे सब बिन्दु हैं जो AB पर या AB से नीचे हैं।
(ii) रेखा x + 4y = 80 बिन्दु C(80, 0), D(0, 20) से होकर जाती है।
असमिका x + 4y ≤ 80 में x = 0, y = 0 रखने पर 0 ≤ 80 जो सत्य है।
मूल बिन्दु इस क्षेत्र में है। इसका हल वे सब बिन्दु हैं जो CD पर यी CD के नीचे स्थित है।
(iii) x = 15 रेखा -अक्ष के समान्तर है और x ≤ 15 का हल वे बिन्दु हैं जो x = 15 पर या इसके बाईं ओर स्थित है।
(iv) y ≥ 0 में y-अक्ष पर और उसके ऊपर के सब बिन्दु हैं।
दी हुई असमिकाओं का हल उभयनिष्ठ क्षेत्र PORS हैं।
प्रश्न 15.
x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0.
हल:
दी हुई सममिकाएँ x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0.
(i) सरल रेखा x + 2y = 10 बिन्दु A(10, 0) और B(0, 5) से होकर जाती है।
असमिका x + 2y ≤ 10 में x = 0, y = 0 रखने पर 0 ≤ 10 जो सत्य है।
मूल बिन्दु इसके क्षेत्र में है।
इस असमिका का हल वे सब बिन्दु हैं जो AB पर हैं तथा AB के नीचे हैं।
(ii) रेखा x + y = 1 बिन्दु C(1,0), D(0, 1) से होकर जाती है।
असमिका x + y ≥ 1 में x = 0, y = 0 रखने पर, 0 ≥ 1 जो सत्य नहीं है।
मूल बिन्दु इसके क्षेत्र में नहीं है।
इस असमिका का हल वे सब बिन्दु हैं जो CD पर हैं या इसके ऊपर हैं।
(iii) रेखा x – y = 0 बिन्दु (0, 0) और (1, 1) से होकर जाती है।
असमिका x – y ≤ 0 में x = 0, y = 0 रखने पर 0 ≤ 0 जो सत्य है।
(0, 0) इसके क्षेत्र में है।
इस असमिका का हल वे बिन्दु जो x – y = 0 पर हैं या इसके ऊपर हैं।
(iv) x ≥ 0 वह क्षेत्र है जो y-अक्ष के दाईं ओर है।
(v) y ≥ 0 वह क्षेत्र है जो x-अक्ष के ऊपर है।
दी हुई असमिकाओं का हल वे सब बिन्दु हैं जो उभयनिष्ठ क्षेत्र PQDB में है।
अध्याय 6 पर विविध प्रश्नावली
प्रश्न 1 से 6 तक की असमिकाओं को हल कीजिए:
प्रश्न 1.
2 ≤ 3x – 4 ≤ 5.
हल:
2 ≤ 3x – 4 ≤ 5
2 + 4 ≤ 3x ≤ 5 + 4
6 ≤ 3x ≤ 9
3 से दोनों पक्षों में भाग देने पर
2 ≤ x ≤ 3
दी हुई असमिका का हल = [2, 3].
प्रश्न 2.
6 ≤ -3 (2x – 4) < 12.
हल:
6 < -3(2x – 4) < 12 6 ≥ -6(x – 2) > 12
-6 से भाग करने पर
-1 ≥ x – 2 > -2;
-1 + 2 ≥ x > -2 + 2
1 ≥ x > 0 या 0 < x ≤ 1
दी हुई असमिका का हल (0, 1].
प्रश्न 7 से 12 तक की असमिकाओं को हल कीजिए और उनके हल को संख्या-रेखा पर निरूपित कीजिए:
प्रश्न 7.
5x + 1 > -24, 5x – 1 < 24.
हल:
(i) 5x + 1 > -24 या 5x > -25 या x > -5
(ii) 5x – 1 < 24 या 5x < 25
x < 5
असमिकाओं का हल (-5, 5).
इसका संख्या रेखा द्वारा निरूपण इस प्रकार है:
प्रश्न 8.
2(x – 1) < x + 5, 3(x + 2) > 2 – x
प्रश्न 9.
3x – 7 > 2(x – 6), 6 – x > 11 – 2x
प्रश्न 10.
5(2x – 7) – 3(2x + 3) ≤ 0, 2x + 19 ≤ 6x + 47.
प्रश्न 11.
एक विलयन को 68°F और 77°F के मध्य रखना है। सेल्सियस पैमाने पर विलयन के तापमान को परिसर ज्ञात कीजिए, जहाँ सेल्सियस फारेनहाइट परिवर्तन सूत्र परिसर ज्ञात कीजिए , जहाँ सेल्सियस फॉरेन्हाइत परिवर्तन सूत्र F =F = C + 32 है।
प्रश्न 12.
8% बोरिक एसिड के विलयन में 2% बोरिक एसिड का विलयन मिलाकर तनु (dilute) किया जाता है। परिणामी मिश्रण में बोरिक एसिड 4% से अधिक तथा 6% से कम होना चाहिए। यदि हमारे पास 8% विलयन की मात्रा 640 लीटर हो तो ज्ञात कीजिए कि 2% विलयन के कितने लीटर इसमें मिलाने होंगे?
हल:
माना 2% बोरिक एसिड का x लीटर विलयन मिलाया जाता है।
कुल मिश्रण की संख्या = 640 + x
(i) यदि मिश्रण में 4% से अधिक का विलयन है तो
x का 2% + 640 का 8% > (640 + x) को 4%
इस प्रकार 2% एसिड विलयन की मात्रा 320 लीटर से अधिक और 1280 लीटर से कम होनी चाहिए।
प्रश्न 13.
45% अम्ल के 1125 लीटर विलयन में कितना पानी मिलाया लाए कि परिणामी मिश्रण में अम्ल 25% से अधिक परन्तु 30% से कम हो जाए?
हल:
मान लीजिए 45% एसिड विलयन में x लीटर पानी मिलाया जाए, तो मिश्रण की कुल मात्रा = (1125 + x) लीटर
(i) (1125 + x) का 25% < 1125 का 45%
प्रश्न 14.
एक व्यक्ति के बोद्धिक-लब्धि (I.Q.) मापन का सूत्र निम्नलिखित है:
IQ = x 100
जहाँ MA मानसिक आयु और CA कालानुक्रमी आयु है। यदि 12 वर्ष की आयु के बच्चों के एक समूह की IQ, असमिका 80 ≤ IQ ≤ 140 द्वारा व्यक्त हो, तो उस समूह के बच्चों की मानसिक आयु का परिसर ज्ञात कीजिए।
एनसीईआरटी सोलूशन्स क्लास 11 गणित-I
- 1. सम्मुच्य
- 2. संबंध एवं फलन
- 3. त्रिकोणमितीय फलन
- 4. गणितीय आगमन का सिद्धांत
- 5. सम्मिश्र संख्याएँ और द्विघातीय समीकरण
- 7. क्रमचय एवं संचय
- 8. द्विपद प्रमेय
- 9. अनुक्रम तथा श्रेणी