NCERT Solutions Class 12 गणित-I Chapter-6 (अवकलज के अनुप्रयोग)

NCERT Solutions Class 12  गणित-I  12 वीं कक्षा से Chapter-6 (अवकलज के अनुप्रयोग) के उत्तर मिलेंगे। यह अध्याय आपको मूल बातें सीखने में मदद करेगा और आपको इस अध्याय से अपनी परीक्षा में कम से कम एक प्रश्न की उम्मीद करनी चाहिए। 

हमने NCERT बोर्ड की टेक्सटबुक्स हिंदी गणित-I के सभी Questions के जवाब बड़ी ही आसान भाषा में दिए हैं जिनको समझना और याद करना Students के लिए बहुत आसान रहेगा जिस से आप अपनी परीक्षा में अच्छे नंबर से पास हो सके।

एनसीईआरटी प्रश्न-उत्तर

Class 12 गणित-I

पाठ-6 (अवकलज के अनुप्रयोग)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

Exercise 6.1

प्रश्न 1.
वृत्त के क्षेत्रफल के परिवर्तन की दर इसकी त्रिज्या r के सापेक्ष ज्ञात कीजिए, जबकि
(a) r = 3 सेमी है
(b) r = 4 सेमी है।
उत्तर
(a) माना वृत्त का क्षेत्रफल A है, तब

अत: क्षेत्रफल के परिवर्तन की दर 6π सेमी²/सेकण्ड है।
(b) उपरोक्त की भाँति स्वयं हल कीजिए।[उत्तर : 8π सेमी²/से]

प्रश्न 2.
एक घन का आयतन 9 सेमी³/से की दर से बढ़ रहा है। यदि इसकी कोर की लम्बाई 10 सेमी है तो इसके पृष्ठ का क्षेत्रफल किस दर से बढ़ रहा है?
उत्तर
माना घन की कोर = x सेमी, घन का आयतन = V तथा पृष्ठ क्षेत्रफल = S
तब V = x³ तथा S = 6x². जहाँ x समय t को फलन है।

अतः पृष्ठ क्षेत्रफल 3.6 सेमी²/से की दर से बढ़ रहा है।

प्रश्न 3.
एक वृत्त की त्रिज्या समान रूप से 3 सेमी/से की दर से बढ़ रही है। ज्ञात कीजिए की वृत्त का क्षेत्रफल किस दर से बढ़ रहा है जब त्रिज्या 10 सेमी है?
उत्तर
मानी वृत्त की त्रिज्या r सेमी है, तब वृत्त का क्षेत्रफल A = πr² सेमी²
प्रश्नानुसार, सेमी/से …(i)

अत: क्षेत्रफल के परिवर्तन की दर 60π सेमी²/सेकण्ड है।

प्रश्न 4.
एक परिवर्तनशील घन का किनारा 3 cm/s की दर से बढ़ रहा है घन का आयतन किस दर से बढ़ रहा है जबकि किनारा 10 cm लम्बा है?
उत्तर
माना घन का आयतन = V तथा भुजा = a है, तब V = a³
ज्ञात है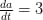
सेमी/से, a = 10 सेमी
∴ समय के सापेक्ष आयतन के परिवर्तन की दर

अतः जब घन का किनारा 10 cm लम्बा हो तब घन का आयतन 900 cm²/s की दर से बढ़ रहा है।

प्रश्न 5.
एक स्थिर झील में एक पत्थर डाला जाता है और तरंगें वृत्तों में 5 सेमी/से की गति से चलती है। जब वृत्ताकार तरंग की त्रिज्या 8 सेमी है तो उस क्षण घिरा हुआ क्षेत्रफल किस दर से बढ़
उत्तर
दिया है- सेमी/से, r = 8 सेमी
माना तरंगों से बने वृत्त का क्षेत्रफल A सेमी² है।
तब A = πr²

अतः जब तरंग की त्रिज्या 8 सेमी हो तब तरंगों द्वारा घिरा हुआ क्षेत्रफल 80 π सेमी²/से की दर से बढ़ रहा है।

प्रश्न 6.
एक वृत्त की त्रिज्या 0.7 सेमी/से की दर से बढ़ रही है। इसकी परिधि की वृद्धि की दर क्या है। जब r = 4.9 सेमी है?
उत्तर
माना वृत्त की त्रिज्या r सेमी है, तब परिधि C = 2πr
प्रश्नानुसार,

अत: वृत्त की परिधि 1.4π सेमी/से की दर से बढ़ रही है।

प्रश्न 7.
एक आयत की लम्बाई x, 5 सेमी/मिनट की दर से घट रही है और चौड़ाई y, 4 सेमी/मिनट की दर से बढ़ रही है। जब x = 8 सेमी और y = 6 सेमी है। तब आयत के
(a) परिमाप
(b) क्षेत्रफल के परिवर्तन की दर ज्ञात कीजिए।
उत्तर
ज्ञात है- सेमी/मिनट
तथा सेमी/मिनट
माना आयत का क्षेत्रफल = A सेमी², परिमाप = p सेमी
लम्बाई = x सेमी, चौड़ाई = y सेमी
(a) परिमाप p = 2(x + y)

अत: आयत का क्षेत्रफल 2 सेमी²/सेमी की दर से बढ़ रहा है।

प्रश्न 8.
एक गुब्बारा जो सदैव गोलाकर रहता है, एक पम्प द्वारा 900 सेमी³/सेकण्ड की दर से फुलाया जाता है। गुब्बारे की त्रिज्या के परिवर्तन की दर ज्ञात कीजिए जब त्रिज्या 15 सेमी है।
उत्तर
माना गुब्बारे की त्रिज्या = r तथा आयतन = V

प्रश्न 9.
एक गुब्बारा जो सदैव गोलाकार रहता है कि त्रिज्या परिवर्तनशील है। त्रिज्या के सापेक्ष आयतन के परिवर्तन की दर ज्ञात कीजिए जब त्रिज्या 10 सेमी है।
उत्तर
माना गुब्बारे का आयतन = V तथा त्रिज्या = r

अतः जब त्रिज्या 10 सेमी हो तब गुब्बारे का आयतन 400 π सेमी³/सेमी की दर से बढ़ता है।

प्रश्न 10.
एक 5 मी लम्बी सीढी दीवार के सहारे झुकी है। सीढ़ी का नीचे का सिरा जमीन के अनुदिश दीवार से दूर 2.0 मी/से की दर से खींचा जाता है। दीवार पर इसकी ऊँचाई किस दर से घट रही है जबकि सीढ़ी को नीचे का सिरा दीवार से 4 मी दूर है?
उत्तर
माना दीवार OC है तथा किसी क्षण सीढ़ी AB की स्थिति इस प्रकार है कि OA = x और OB = y

अत: दीवार पर सीढ़ी की ऊँचाई 8/3 मी/से की दर से घट रही है।

प्रश्न 11.
एक कण वक्र 6y = x³ + 2 के अनुगत गति कर रहा है। वक्र पर उन बिन्दुओं को ज्ञात कीजिए जबकि x निर्देशांक की तुलना में y निर्देशांक 8 गुना तीव्रता से बदल रहा है।
उत्तर
दिया है-
6y = x³ + 2 और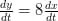 
t के सापेक्ष अवकलन करने पर,

प्रश्न 12.
हवा के बुलबुले की त्रिज्या, सेमी/सेकण्ड की दर से बढ़ रही है। बुलबुले का आयतन किस दर से बढ़ रहा है जबकि त्रिज्या 1 सेमी है?
उत्तर
माना बुलबुले की त्रिज्या = r तथा बुलबुले का आयत


अत: बुलबुले का आयतन 2π सेमी³/से की दर से बढ़ रहा है।

प्रश्न 13.
एक गुब्बारा जो सदैव गोलाकार रहता है, का परिवर्तनशील व्यास है। x के सापेक्ष आयतन के परिवर्तन की दर ज्ञात कीजिए।
उत्तर
प्रश्नानुसार गोलाकार गुब्बारे का व्यास = 

प्रश्न 14.
एक पाइप से रेत 12 सेमी³/से की दर से गिर रही है। गिरती रेत जमीन पर एक ऐसा शंकु बनाती है जिसकी ऊँचाई सदैव आधार की त्रिज्या का छठा भाग है।रेत से बने शंकु की ऊँचाई किस दर से बढ़ रही है जबकि ऊँचाई 4 सेमी है?
उत्तर
माना किसी क्षण t है पर शंकु की त्रिज्या r, ऊँचाई h तथा आयतन V है।

⇒ r = 6h

प्रश्न 15.
एक वस्तु की x इकाइयों के उत्पादन की कुल लागत C (x) Rs में
C(x) = 0.007x³ – 0.003x² + 15x + 4000
से प्राप्त होती है। सीमान्त लागत ज्ञात कीजिए जबकि 17 इकाइयों का उत्पादन किया जाता है।
उत्तर
प्रश्नानुसार, C(x) = 0.007x³ – 0.003x² + 15x + 4000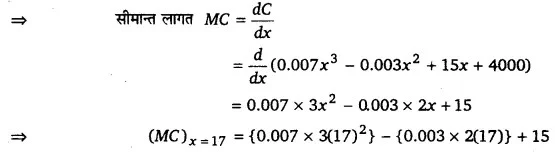

= 6.069 – 0.102 + 15
= 20.967
अतः 17 इकाइयों के उत्पादन की सीमान्त लागत Rs 20.967 है।

प्रश्न 16.
किसी उत्पाद की x इकाइयों के विक्रय से प्राप्त कुल आय R(x) Rs में R(x) = 13x² + 26x + 15 से प्राप्त होती है। सीमान्त आय ज्ञात कीजिए जब x = 7 है।
उत्तर
प्रश्नानुसार, R(x) = 13x² + 26x + 15

(MR)_x=7 = 26 x 7 + 26
= 182 + 26
= 208
अत: अभीष्ट सीमान्त आय Rs 208 है।

प्रश्न 17.
एक वृत्त की त्रिज्या r = 6 सेमी पर r के सापेक्ष क्षेत्रफल में परिवर्तन की दर है :
(a) 10 π
(b) 12 π
(c) 8 π
(d) 11 π
उत्तर
मानी वृत्त का क्षेत्रफल = A तथा त्रिज्या = r
क्षेत्रफल A = πr²

अत: विकल्प (b) सही है।

प्रश्न 18.
एक उत्पाद की x इकाइयों के विक्रय से प्राप्त कुल आय रुपयों में R(x) = 3x² + 36x + 5 से प्रदत्त है। जब x = 15 है तो सीमान्ते आये है :
(a) 116
(b) 96
(c) 90
(d) 126
उत्तर
दिया है- R(x) = 3x² + 36x +5
सीमान्त ।
सीमान्त आय =

अब, x = 15, सीमान्त आय = 6 × 21 = Rs 126
अत: विकल्प (d) सत्य है।

Exercise 6.2

प्रश्न 1.
दिखाइए कि दिया गया फलन f, f(x) = x³ – 3x² + 4x, x ∈ R, R पर निरन्तर वृद्धिमान फलन है।
उत्तर
दिया गया फलन
f(x) = x³ – 3x² + 4x
f ‘(x) = 3x² – 6x +4

= 3(x – 1)² + 1 > 0, ∀ x∈R
∵ f ‘(x) > 0, ∀ x∈R
∴ f(x), R पर निरन्तर वृद्धिमान फलन है।

प्रश्न 2.
सिद्ध कीजिए कि R पर f(x) = 3x + 17 निरन्तर वृद्धिमान फलन है।
उत्तर
दिया गया फलन f(x) = 3x + 17
f ‘(x) = 3 > 0, ∀ x∈R
f ‘(x) > 0, ∀ x∈R
∴ f(x), R पर निरन्तर वृद्धिमान फलन है।

प्रश्न 3.
सिद्ध कीजिए कि f(x) = sin x द्वारा दिया गया फलन
(a) (0, π/2) में निरन्तर वृद्धिमान है।
(b) (π/2, π) में निरन्तर ह्रासमान है।
(c) (0, π) में न तो वृद्धिमान है और न ह्रासमान।
उत्तर
(a) f(x) = sin x
⇒ f ‘(x) = cos x

अन्तराल (0, π/2) में निरन्तर वृद्धिमान तथा अन्तराल (π/2, π) में निरन्तर ह्रासमान है।
∴ फलन अन्तराल (0, π) में न तो वृद्धिमान है और न ह्रासमान,

प्रश्न 4.
अन्तराल ज्ञात कीजिए जिनमें f(x) = 2x² – 3x द्वारा दिया गया फलन
(a) निरन्तर वृद्धिमान है,
(b) निरन्तर ह्रासमान है।
उत्तर
(a) दिया गया फलन f(x) = 2x² – 3x
f ‘(x) = 4x – 3 > 0, ∀ x > 
∴ f(x), अन्तराल (3/4, ∞) पर निरन्तर वृद्धिमान है।
(b) पुनः f ‘(3) = 4x – 3< 0, ∀ x < 
∴ f(x), अन्तराल (-∞,3/4) पर निरन्तर ह्रासमान है।

प्रश्न 5.
अन्तराल ज्ञात कीजिए जिनमें f(x) = 2x³ – 3x² – 36x + 7 से दिया फलन f (a) निरन्तर वृद्धिमान है, (b) निरन्तर ह्रासमान है।
उत्तर
(a) दिया गया फलन f(x) = 2x³ – 3x² – 36x +7
f ‘(x) = 6x² – 6x – 36 = 6(x² – x – 6).

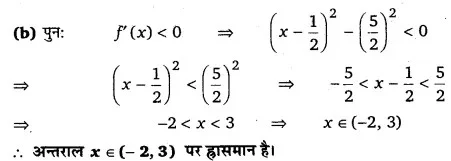
प्रश्न 6.
अन्तराल ज्ञात कीजिए जिनमें निम्नलिखित फलन निरन्तर वर्धमान अथवा हासमान है
(a) f(x) = x² + 2x + 5
(b) f (x) = 10 – 6x – 2x²
(c) f (x) = – 2x³ – 9x² – 12x + 1
(d) f(x) = 6 – 9x – x²
(e) f(x) = (x + 1)³ (x – 3)³
उत्तर
(a) ज्ञात है- f (x) = x² + 2x + 5
f ‘ (x) = 2x + 2 = 2 (x + 1)
f ‘ (x) = 0 ⇒ 2 (x + 1) ⇒ x = – 1
x = – 1 संख्या रेखा को दो भागों में बांटता है। यह भाग अन्तराल (-∞ , -1) तथा (-1, ∞ ) है।
(- ∞ , – 1) में f ‘ (x) = – ऋणात्मक
अत: अन्तराल (-∞ , -1) में फलन f निरन्तर ह्रासमान है।
(-1, ∞ ) में f ‘ (x) = + धनात्मक
अतः अन्तराल (-1, ∞ ) फलन f निरन्तर वर्धमान है।
(b) ज्ञात है. f (x) = 10 – 6x – 2x²
f ‘ (x) = – 6 – 4x = – 2 (3 + 2x)

प्रश्न 7.
सिद्ध कीजिए कि

अपने सम्पूर्ण प्रान्त में एक वृद्धिमान फलन है।
उत्तर
दिया गया फलन

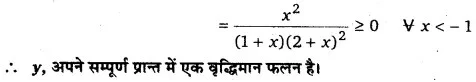
प्रश्न 8.
x के उन मानों को ज्ञात कीजिए जिनके लिए y = [x(x – 2)]² एक वर्धमान फलन है।
उत्तर
ज्ञात है- y = [x (x – 2)]² = x² (x + 4 – 4x)
= x⁴ – 4x³ + 4x²
x के सापेक्ष अवकलन करने पर,

∴ x = 0, x = 1, x = 2 से वास्तविक संख्या रेखा के चार भाग अन्तराल (-∞, 0), (0, 1), (1, 2), (2, 2) बनते हैं।
अन्तराल (- ∞, 0) में f ‘ (x) = (-) (-) (-) = – ve (ऋणात्मक)
अतः फलन f निरन्तर ह्रासमान है।
अन्तराल (0, 1) में f ‘ (x) = (+) (-) (-) = + ve (धनात्मक)
अतः फलन f निरन्तर वर्धमान है।
अन्तराल (1, 2) में f ‘ (x) = (+) (+) (-) = – ve (ऋणात्मक)
अतः फलन f निरन्तर ह्रासमान है।
अन्तराल (2, ∞) में f ‘ (x) = (+) (+) (+) = +ve (धनात्मक)
अतः फलन f निरन्तर वर्धमान है।
इस प्रकार (0, 1) ∪ (2, ∞) में फलन f वर्धमान है तथा (-∞, 0) ∪ (1, 2) में फलन ह्रासमान है।

प्रश्न 9.
सिद्ध कीजिए कि [0, π/2] में

θ का एक वृद्धिमान फलन है।
उत्तर

प्रश्न 10.
सिद्ध कीजिए कि लघुगणकीय फलन (0,∞) में निरन्तर वर्धमान फलन है।
उत्तर
ज्ञात है– f (x) = log x, x > 0
f ‘(x) = = धनात्मक, x > 0 के लिए
अतः लघुगणकीय फलन अन्तराल (0, ∞) के लिए निरन्तर वर्धमान है। इति सिद्धम्

प्रश्न 11.
सिद्ध कीजिए कि (-1,1) में f (x) = x² – x + 1 से प्रदत्त फलन न तो वर्धमान है। और न ही ह्रासमान है।
उत्तर
दिया है | f (x) = x² – x + 1


इस प्रकार (-1, 1) में f ‘(x) का चिह्न एक नहीं है।
अतः इस अन्तराल में यह फलन न तो वर्धमान है और न ही ह्रासमान है। इति सिद्धम्

प्रश्न 12.
निम्नलिखित में कौन से फलन (0,) में निरन्तर ह्रासमान है?
(A) cos x
(B) cos 2x
(C) cos 3x
(D) tan x
उत्तर-
(A) माना f (x) = cos x, ∴ f ‘ (x) = – sin x
अन्तराल (0, π/ 2) में, sin x = + धनात्मक ⇒f ‘ (x) = – ऋणात्मक
अतः फलन f निरन्तर ह्रासमान है।
(B) माना f (x) = cos 2x
∴ f ‘(x) = – 2 sin 2x

प्रश्न 13.
निम्नलिखित अन्तरालों में से किस अन्तराल में f (x) = x¹⁰⁰ + sin x – 1 द्वारा प्रदत्त फलन f निरन्तर ह्रासमान है ?

उत्तर-

प्रश्न 14.
a का वह न्यूनतम मान ज्ञात कीजिए जिसके लिए अन्तराल [1, 2] में f(x) = x² + ax + 1 से दिया गया फलन निरन्तर वृद्धिमान है।
उत्तर-
दिया गया फलन
f(x) = x² + ax + 1
f ‘(x) = 2x + a
अन्तराल [1, 2] में f ‘(x) का न्यूनतम मान f ‘(1) = 2 + a होगा
∵ f(x) अन्तराल [1, 2] में निरन्तर वृद्धिमान है ∴ f ‘(x) ≥ 0
∴ 2 + a ≥ 0
⇒ a≥ -2
अत: a का न्यूनतम मान -2 है।

प्रश्न 15
माना[-1, 1] से असंयुक्त एक अन्तराल I हो तो सिद्ध कीजिए कि I में f(x) = से दिया गया फलन f निरन्तर वृद्धिमान है।
उत्तर-
दिया गया फलन f(x) = 

∴ (x – 1)(x + 1) > 0
∴ f ‘(x) > 0
⇒ f(x) निरन्तर वृद्धिमान है जब x∈ (1, ∞)
अतः f(x), I पर निरन्तर वृद्धिमान है।

प्रश्न 16.
सिद्ध कीजिए कि फलन f(x) = log sin x,(0,) में निरन्तर वर्धमान और (,π) में निरन्तर ह्रासमान है।
उत्तर-
दिया है- f(x) = log sin x

प्रश्न 17.
सिद्ध कीजिए कि फलन f(x) = log | cos x|; (0, π/2) निरन्तर ह्रासमान और (π/2, π) में निरन्तर वृद्धिमान है।
उत्तर-
दिया गया फलन f(x) = log cos x

प्रश्न 18.
सिद्ध कीजिए कि R में दिया गया फलन f(x) = x³ – 3x² + 3x – 100 वर्धमान है।
उत्तर-
ज्ञात है- f (x) = x³ – 3x² + 3x – 100
∴f ‘(x) = 3x² – 6x + 3 = 3 (x² – 2x + 1) = 3(x – 1)²
∀x∈ R, f ’(x) = धनात्मक
अतः फलन f वर्धमान है। इति सिद्धम्

प्रश्न 19.
निम्नलिखित में से किस अन्तराल में y = x²e^-x वर्धमान है?
(a) (-∞, ∞)
(b) (-2, 0)
(c) (2, ∞)
(d) (0, 2)
उत्तर-
दिया है- f (x) = x²e^-x

Exercise 6.3

प्रश्न 1.
वक्र y = 3x⁴ – 4x के x = 4पर स्पर्श रेखा की प्रवणता ज्ञात कीजिए।
उत्तर-
दिया है, वक्र का समीकरण y = 3x⁴ -4x

= 4[3 x 64 – 1]
= 4[192 – 1]
= 4 x 191
= 764
∴स्पर्श रेखा की प्रवणता = 764

प्रश्न 2.
वक्र ,x ≠ 2 के x = 10 पर स्पर्श रेखा की प्रवणता ज्ञात कीजिए।
उत्तर-
दिया है, वक्र का समीकरण ,x ≠ 2
दोनों पक्षों का x के सापेक्ष अवकलन करने पर

प्रश्न 3.
वक्र y = x³ – x + 1 की स्पर्श रेखा की प्रवणता उस बिन्दु पर ज्ञात कीजिए जिसका x-निर्देशांक 2 है।
उत्तर-
दिया है, वक्र का समीकरण y = x³ – x + 1

प्रश्न 4.
वक्र y = x³ – 3x + 2 की स्पर्श रेखा की प्रवणता उस बिन्दु पर ज्ञात कीजिए जिसका x – निर्देशांक 3 है।
उत्तर-

प्रश्न 5.
वक्र x = a cos³θ, y= a sin³θ के θ = पर अभिलम्ब की प्रवणता ज्ञात कीजिए।
उत्तर-
दिया है, वक्र को समीकरण x = a cos³θ तथा y = a sin³θ
दोनों पक्षों का θ के सापेक्ष अवकलन करने पर,

प्रश्न 6.
वक्र x = 1 – a sin θ, y = b cos² θ के θ = पर अभिलम्ब की प्रवणता ज्ञात कीजिए।
उत्तर-
दिया है, वक्र का समीकरण x = 1 – a sin θ तथा y = b cos² θ
दोनों पक्षों का θ के सापेक्ष अवकलन करने पर,

प्रश्न 7.
वक्र y = x³ – 3x² – 9x + 7 पर उन बिन्दुओं को ज्ञात कीजिए जिन पर स्पर्श रेखायें x-अक्ष के समान्तर हैं।
उत्तर-

प्रश्न 8.
वक्र y = (x – 2)² पर एक बिन्दु ज्ञात कीजिए जिस पर स्पर्श रेखा बिन्दुओं (2,0) और (4,4) को मिलाने वाली रेखा के समान्तर है।
उत्तर-
दिया है, वक्र का समीकरण y = (x – 2)²
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

प्रश्न 9.
वक्र y = x³ – 11x + 5 पर उस बिन्दु को ज्ञात कीजिए जिस पर स्पर्श रेखा y = x – 11 है।
उत्तर-
दिया है, वक्र का समीकरण y = x³ – 11x + 5

प्रश्न 10.
प्रवणता -1 वाली सभी रेखाओं का समीकरण ज्ञात कीजिए जो वक़ 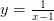,x ≠ -1 को स्पर्श करती है।
उत्तर-
दिया है, वक्र का समीकरण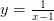 

प्रश्न 11.
प्रवणता 2 वाली सभी रेखाओं का समीकरण ज्ञात कीजिए जो वक्र ,x ≠ 3 को स्पर्श करती है।
उत्तर
दिया है, वक्र का समीकरण 
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

प्रश्न 12.
प्रवणता 0 वाली सभी रेखाओं का समीकरण ज्ञात कीजिए जो वक्र

को स्पर्श करती है।
उत्तर
दिया है, वक्र का समीकरण

दोनों पक्षों को x के सापेक्ष अवकलन करने पर,

प्रश्न 13.
वक्र

पर उन बिन्दुओं को ज्ञात कीजिए जिन पर स्पर्श रेखाएँ
(i) x-अक्ष के समान्तर हैं,
(ii) y-अक्ष के समान्तर हैं।
उत्तर
दिया है, वक्र का समीकरण

दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

प्रश्न 14.
दिए वक्रों पर निर्दिष्ट बिन्दुओं पर स्पर्श रेखा और अभिलम्ब के समीकरण ज्ञात कीजिए
(i) y = x⁴ – 6x³ + 13x² – 10x + 5 के (0, 5) पर
(ii) y = x⁴ – 6x³ + 13x² – 10x + 5 के (1, 3) पर
(iii) y = x³ के (1, 1) पर .
(iv) y = x² के (0, 0) पर
(v) x = cost, y = sin t के पर
उत्तर

प्रश्न 15.
वक्र y = x² – 2x + 7 की स्पर्श रेखा का समीकरण ज्ञात कीजिए, जो
(a) रेखा 2x – y + 9 = 0 के समान्तर है।
(b) रेखा 5y – 15x = 13 पर लम्ब है।
उत्तर-
दिया है, वक्र का समीकरण y = x² – 2x + 7
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

प्रश्न 16.
सिद्ध कीजिए कि वक्र y = 7x³ + 11 के उन बिन्दुओं पर स्पर्श रेखाएँ समान्तर हैं जहाँ x = 2 तथा x = – 2 है।
उत्तर-
दिया है, वक्र का समीकरण y = 7x³ + 11
दोनों पक्षों का x के सापेक्ष अवकलन करने पर, = 21 x²
जब x = 2, तब स्पर्श रेखा की प्रवणता = 21 x 2² = 21 x 4 = 84
जब x = -2, तब स्पर्श रेखा की प्रवणता = 21 x (-2)² = 84
x = 2 तथा x = -2 पर स्पर्श रेखा की प्रवणता समान हैं।
अतः इन बिन्दुओं पर स्पर्श रेखाएँ समान्तर हैं। इति सिद्धम्

प्रश्न 17.
वक्र y = x³ पर उन बिन्दुओं को ज्ञात कीजिए जिन पर स्पर्श रेखा की प्रवणता बिन्दु के y-निर्देशांक के बराबर है।
उत्तर-
दिया है, वक्र की समीकरण y = x³
दोनों पक्षों का x के सापेक्ष अवकलन करने पर, = 3x²

प्रश्न 18.
वक्र y = 4x³ – 2x⁵, पर उन बिन्दुओं को ज्ञात कीजिए जिन पर स्पर्श रेखाएँ मूलबिन्दु से होकर जाती हैं।
उत्तर-
दिया है, वक्र का समीकरण y = 4x³ – 2x⁵

प्रश्न 19.
वक्र x² + y² – 2x – 3 = 0 के उन बिन्दुओं पर स्पर्श रेखाओं के समीकरण ज्ञात कीजिए जहाँ पर वे x-अक्ष के समान्तर हैं।
उत्तर-
दिया है, वक्र का समीकरण x² + y² – 2x – 3 = 0
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

प्रश्न 20
वक्र ay² = x³ के बिन्दु (am², um³)पर अभिलम्ब का समीकरण ज्ञात कीजिए और m का मान बताइए जिसके लिए अभिलम्ब बिन्दु (a, 0) से होकर जाता है।
उत्तर-
वक्र ay² = x³ ….(1)
समीकरण (1) का x के सापेक्ष अवकलन करने पर,

प्रश्न 21

उत्तर-

प्रश्न 22.
परवलय y² = 4ax के बिन्दु (at², 2at) पर स्पर्श रेखा और अभिलम्ब के समीकरण ज्ञात कीजिए।
उत्तर-
दिया है, वक्र का समीकरण y² = 4ax
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

प्रश्न 23

उत्तर-

प्रश्न 24.
अतिपरवलय के बिन्दु (x₀, y₀) पर स्पर्श रेखा तथा अभिलम्ब के समीकरण ज्ञात कीजिए।
उत्तर-
दिया है, वक्र का समीकरण 
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

प्रश्न 25.
वक्र की उन स्पर्श रेखाओं के समीकरण ज्ञात कीजिए जो रेखा 4x – 2y + 5 = 0 के समान्तर है।
उत्तर-
दिया है, वक्र का समीकरण …(1)
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

प्रश्न 26.
वक्र y = 2x² + 3sin x के x = 0 पर अभिलम्ब की प्रवणता है
(A) 3
(B) 
(C) 3
(D) 
उत्तर-
दिया है, वक्र का समीकरण y = 2x² + 3 sin x
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,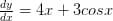 

अतः विकल्प (D) सही है।

प्रश्न 27.
किस बिन्दु पर y = x + 1, वक्र y² = 4x की स्पर्श रेखा है?
(A) (1,2)
(B) (2,1)
(C) (1,- 2)
(D) (-1, 2)
उत्तर-
दिया है, वक्र का समीकरण y² = 4x …(1)
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

Exercise 6.4

प्रश्न 1.
अवकल का प्रयोग करके निम्नलिखित में से प्रत्येक का सन्निकट मान दशमलव के तीन स्थानों तक ज्ञात कीजिए
(i) 
(ii) 
(iii) 
(iv) (0.009)^1/3
(v) (0.999)^1/10
(vi) (15)^1/4
(vii) (26)^1/3
(viii) (255)^1/4
(ix) (82)^1/4
(x) (401)^1/2
(xi) (0.0037)^1/2
(xii) (26.57)^1/3
(xiii) (81.5)^1/4
(xiv) (3,968)^3/2
(xv) (32.15)^1/5
उत्तर-

प्रश्न 2.
f(2.01) का सन्निकट मान ज्ञात कीजिए जबकि f(x) = 4x² + 5x + 2
उत्तर-
माना x = 2 और x + ∆x = 2.01 तब ∆x = 0.01 = dx (∵∆Y = dx)

प्रश्न 3.
f(5.001) का सन्निकट मान ज्ञात कीजिए जहाँ f(x) = x³ – 7 x² + 15
उत्तर-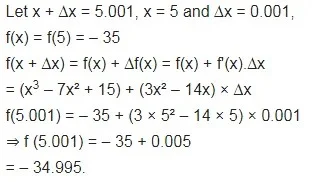

प्रश्न 4.
x मी भुजा वाले घन की भुजा में 1% की वृद्धि होने के कारण घन के आयतन में होने वाला सन्निकट परिवर्तन ज्ञात कीजिए।
उत्तर-
माना घन का आयतन V = x³

घन के आयतन में सन्निकट परिवर्तन 0.03 x³ मी है।

प्रश्न 5.
x मी भुजा वाले घन की भुजा में 1% ह्रास होने के कारण घन के पृष्ठ क्षेत्रफल में होने वाला सन्निकट परिवर्तन ज्ञात कीजिए।
उत्तर
घन का पृष्ठ क्षेत्रफल S = 6x²


घन के आयतन में सन्निकट परिवर्तन -0.12 x² मी² है।

प्रश्न 6.
एक गोले की त्रिज्या 7 मी मापी जाती है जिसमें 0.02 मी की त्रुटि है। इसके आयतन के परिकलन में सन्निकट त्रुटि ज्ञात कीजिए।
उत्तर
ज्ञात है- गोले की त्रिज्या = 7 मी ।
∆r = त्रिज्या में अशुद्धि = 0.02 मी

प्रश्न 7.
एक गोले की त्रिज्या 9 मी मापी जाती है जिसमें 0.03 मी की त्रुटि है। इसके पृष्ठ क्षेत्रफल के परिकलन में सन्निकट त्रुटि ज्ञात कीजिए।
उत्तर
ज्ञात है- r = गोले की त्रिज्या = 9 मी
∆r = त्रिज्या में अशुद्धि = 0.03

प्रश्न 8.
यदि f (x) = 3x² + 15x + 5 हो तो f (3.02) का सन्निकट मान है–
(A) 47.66
(B) 57.66
(C) 67.66
(D) 77.66
उत्तर
f (3.02) = f (3) + df (3) [3.02 = 3 + 0.02]
यदि f (x) = 3x² + 15x + 5 …(1)
f ‘(x) = 6x + 15
समी० (1) में x = 3 रखने पर,
f (3) = 3 x 9 + 15 x 3 + 5 = 27 + 45 + 5 = 77
df (x) = f ‘(x) x ∆x = (6x + 15) x ∆x
= (6 x 3 + 15) x 0.02 [∴ x = 3, ∆ x = 0.02]
= (18 + 15) x 0.02
= 33 x 0.02 = 0.66
∴ f (3.02) = f (3) + df (3) = 77 + 0.66 = 77.66
अत: विकल्प (D) सही है।

प्रश्न 9.
भुजा में 3% वृद्धि के कारण भुजा x के घन के आयतन में सन्निकट परिवर्तन है
(A) 0.06 x³ मी³
(B) 0.6 x³ मी³
(C) 0.09 x³ मी³
(D) 0.9 x³ मी³
उत्तर
चूँकि घन का आयतन V = x³ (∵ भुजा = x मी)
भुजा में वृद्धि, ∆x = 3% = x का


अत: विकल्प (C) सही है।

Exercise 6.5

प्रश्न 1.
निम्नलिखित दिए गए फलनों के उच्चतम या निम्नतम मान, यदि कोई हो तो ज्ञात कीजिए
(i) f (x) = (2x – 1)² + 3
(ii) f (x) = 9x² + 12x + 2
(iii) f (x) = -(x – 1)² + 10
(iv) g(x) = x³ + 1
उत्तर
(i) दिया गया फलन f(x) = (2x – 1)² + 3
(2x – 1)² का कम-से-कम मान = 0,
⇒ f(x) ≥ 3; ∀ x∈R
∴ f (x) का निम्नतम मान = 3
(ii) दिया गया फलन f (x) = 9x² + 12x + 2 = 9x² + 12x + 4 – 2
= (3x + 2)² – 2
(3x + 2)² का निम्नतम मान = 0,
⇒ f (x) ≥ -2; ∀ x∈R
∴ f (x) का निम्नतम मान = -2
(iii) दिया गया फलन f (x) = – (x – 1)² + 10
– (x – 1)² का उच्चतम मान = 0
⇒f (x) ≤ 10; ∀ x∈R
∴f का उच्चतम मान = 10
(iv) यहाँ g(x) = x³ + 1.
g ‘(x) = 3x² जो x ∈ R के लिए धनात्मक है।
g ‘(x) = 3x² ≥ 0; ∀ x∈R
अत: g एक वर्धमान फलन है।
∴ इसका कोई न्यूनतम तथा अधिकतम मान नहीं है।

प्रश्न 2.
निम्नलिखित दिए गए फलनों के उच्चतम मान या निम्नतम मान, यदि कोई हो तो ज्ञात कीजिए
(i) f(x) = |x + 2| – 1
(ii) g(x) = -|x + 1| + 3
(iii) h(x) = sin (2x) + 5
(iv) f(x) =|sin 4x + 3|
(v) h(x) = x + 1, x∈(-1,1)
उत्तर
(i) दिया गया फलन f(x) =|x + 2| – 1, f (x)≥ -1; ∀ x∈R
|x + 2| को निम्नतम मान 0 है।
∴ f का निम्नतम मान = -1
|x + 2| कर उच्चतम मान अनन्त हो सकता है।
अत: उच्चतम मान का अस्तित्व नहीं है।
(ii) दिया गया फलन g(x) = -|x + 1| + 3; g (3) ≤ 3∀ x∈R
-|x +1| का उच्चतम मान = 0
g(x) = -|x + 1| + 3 का उच्चतम मान = 0 + 3 = 3
तथा निम्नतम मान का अस्तित्व नहीं है।
(iii) दिया गया फलन h(x) = sin (2x) + 5
हम जानते हैं कि -1 ≤ sin 2x ≤ 1
⇒ 4 ≤ 5 + sin 2x ≤ 6
sin 2x का उच्चतम मान = 1

प्रश्न 3
निम्नलिखित फलनों के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।

उत्तर
(i) दिया गया फलन f(x) = x²
⇒ f ‘(x) = 2x
यदि f ‘(x) = 0 तब 2x = 0 या x = 0
f ‘(x) जैसे ही x = 0 से होकर आगे बढ़ता है तब इसका चिह्न ऋणात्मक से धनात्मक में बदल जाता है।
∴x = 0 पर f स्थानीय मान निम्नतम है।
स्थानीय निम्नतम मान = f (0) = 0

प्रश्न 4
सिद्ध कीजिए कि निम्नलिखित फलनों को उच्चतम या निम्नतम मान नहीं है–
(i) f (x) = e^x
(ii) g(x) = log x
(iii) h(x) = x³ + x² + x + 1
उत्तर
(i) दिया गया फलन f ‘(x) = e^x
∴f ‘(x) = e^x
f ‘(x), x∈R कभी भी शून्य के समान नहीं है।
अत: f का कोई उच्चतम या निम्नतम मान नहीं है। इति सिद्धम्

प्रश्न 5
प्रदत्त अन्तरालों में निम्नलिखित फलनों के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए

उत्तर
(i) दिया गया फलन f(x) = x³, अन्तराल [-2, 2]
f ‘(x) = 3x²
यदि f ‘(x) = 0, तब 3x² = 0
⇒ x = 0
x = -2 पर, f(-2) = (-2)³ = – 8
x = 0 पर, f(0) = (0)³ = 0

प्रश्न 6
यदि लाभ फलन p(x) = 41 – 72x – 18x² से प्रदत्त है तो किसी कम्पनी द्वारा अर्जित उच्चतम लाभ ज्ञात कीजिए।
उत्तर
दिया गया फलन लाभ p(x) = 41 -72x – 18x² …(1)
p’ (x) = – 72 – 36x = – 36 (2 + x)
p ” (x) = – 36
यदि p ‘(x) = 0, तब – 36 (2 + x) = 0 ⇒ 2 + x = 0 ∴ x = -2
p ‘(x) = – ve
अतः x = -2 पर p(x) उच्चतम है।
∴उच्चतम लाभ = p(-2)
[समी० (1) में x  = -2 रखने पर]
= 41 – 72 (-2)² – 18 (-2)²
= 41 + 144 – 72
= 43 इकाई

प्रश्न 7
अन्तराल [0, 3] पर 3x⁴ – 8x³ + 12x² – 48x + 25 के उच्चतम मान और निम्नतम मान ज्ञात कीजिए।
उत्तर
माना f (x) = 3x⁴ – 8x³ + 12x² – 48x + 25
f ‘(x) = 12x³ – 24x² + 24x – 48
= 12 [x³ – 2x² + 2x – 4] = 12 [x² (x – 2) + 2 (x – 2)]
= 12 (x – 2) (x² + 2)
यदि f ‘(x) = 0, तब x – 2 = 0 ⇒ x = 2

प्रश्न 8
अन्तराल [0, 2π] के किन बिन्दुओं पर फलन sin 2 x अपना उच्चतम मान प्राप्त करता है।
उत्तर
माना f (x) = sin 2x, अन्तराल [0, 2π]
f ‘(x) = 2 cos 2x

प्रश्न 9.
फलन sin x + cos x का उच्चतम मान क्या है?
उत्तर
माना f (x) = sin x + cos x, अन्तराल [0, 2π]
f ‘(x) = cos x – sin x
उच्चतम व निम्नतम मान के लिए,

प्रश्न 10.
अन्तराल [1,3] में 2x³ – 24x + 107 का महत्तम मान ज्ञात कीजिए। इसी फलन का अन्तराला [-3,-1] में भी महत्तम मान ज्ञात कीजिए।
उत्तर
माना
f (x) = 2x³ – 24x + 107, अन्तराल [1, 3]
f ‘(x) = 6x² – 24
उच्चतम व निम्नतम मान के लिए, f ‘(x) = 0
⇒ 6x² – 24 = 0 ⇒ 6x² = 24 ⇒ x² = 4 ⇒ x = ±2
अन्तराल [1, 3] के लिए f(x) = 2x³ – 24x + 107 में x के मान रखने पर,
x = 1 पर, f(1) = 2(1)³ – 24 (1) + 107 = 2 – 24 + 107 = 85
x = 3 पर, f (3) = 2(3)³ – 24 (3) + 107 = 54 – 72 + 107 = 89
x = 2 परे, f(2) = 2(2)³ – 24(2) + 107 = 16 – 48 + 107 = 75
इस प्रकार अधिकतम मान f (x) = 89,
x = 3 पर, अन्तराल [-3,-1] के लिए हम x = – 3, – 2, – 1 पर f(x) का मान ज्ञात करते हैं।
x = – 3 पर, f(-3) = 2(-3)³ – 24 (-3) + 107
= – 54 + 72 + 107 = – 54 + 179 = 125
x = – 1 पर f(-1) = 2 (-1)³ – 24 (-1) + 107 = -2 +24 + 107 = 129
x = – 2 पर f(-2) = 2(-2)³ – 24 (-2) + 107 = -16 + 48 +107 = 139
इस प्रकार अधिकतम मान f (x) = 139, x = -2 पर।

प्रश्न 11.
यदि दिया है कि अन्तराल [0,2] में x = 1 पर फलन x⁴ – 62x² + ax + 9 उच्चतम मान प्राप्त करता है तो a का मान ज्ञात कीजिए।
उत्तर
माना f(x) = x⁴ – 62x² + ax + 9
f ‘(x) = 4x³ – 124x + a
उच्चतम व निम्नतम मान के लिए, f ‘(x) = 0
⇒ 4x³ – 124x + a = 0
दिया है, x = 1 पर, f उच्चतम है ⇒ f (1) = 0
4x³ – 124x + a = 0 में x = 1 रखने पर
4 x 1 – 124 x 1 + a = 0 ⇒ 4 – 124 + a = 0 ⇒ – 120 + a = 0
a = 120
इसलिए a का मान 120 है।

प्रश्न 12.
[0,2π] पर x + sin 2x का उच्चतम और निम्नतम मान ज्ञात कीजिए।
उत्तर
माना f(x) = x + sin 2x
f ‘(x) = 1 + 2 cos 2x
उच्चतम व निम्नतम मान के लिए, f ‘(x) = 0
⇒ 1 + 2 cos 2x = 0 ⇒ cos2x = 

प्रश्न 13.
ऐसी दो संख्याएँ ज्ञात कीजिए जिनका योग 24 है और जिनका गुणनफल उच्चतम हो।
उत्तर
माना पहली संख्या = x तब दूसरी संख्या = 24 – x है।
प्रश्नानुसार, उनका गुणनफल p = x(24 – x) = 24x – x² …(1)
उच्चतम व निम्नतम मान के लिए,
समी० (1) का x के सापेक्ष अवकलन करने पर,

प्रश्न 14.
ऐसी दो धन संख्याएँ x और y ज्ञात कीजिए ताकि x + y = 60 और xy³ उच्चतम हो।
उत्तर
दिया है,
x + y = 60
x = 60 – y …(1)
माना xy³ = P …(2)
समीकरण (1) से x का मान समीकरण (2) में रखने पर,

प्रश्न 15.
ऐसी दो धन संख्याएँ x और y ज्ञात कीजिए जिनका योग 35 हो और गुणनफल x²y⁵ उच्चतम हो।
उत्तर
दो धन संख्याएँ x, y हैं।
दिया है, x + y = 35
⇒ y = 35 – x …(1)
प्रश्नानुसार, माना गुणनफल p = x²y⁵ …(2)
समीकरण (1) से y का मान समीकरण (2) में रखने पर,
p = x² (35 – x)⁵
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

प्रश्न 16.
ऐसी दो धन संख्याएँ ज्ञात कीजिए जिनका योग 16 हो और जिनके घनों का योग निम्नतम हो।
उत्तर

प्रश्न 17.
18 सेमी भुजा के टिन के किसी वर्गाकार टुकड़े से प्रत्येक कोने पर एक वर्ग काटकर तथा इस प्रकार बने टिन के फलकों को मोड़कर ढक्कन रहित एक सन्दूक बनाना है। काटे जाने वाले वर्ग की भुजा कितनी होगी जिससे सन्दूक का आयतन उच्चतम होगा?
उत्तर
माना वर्ग की प्रत्येक भुजा x सेमी काटी गई है।
∴ सन्दूक के लिए,
लम्बाई = 18 – 2x
चौड़ाई = 18 – 2x
ऊँचाई = x
आयतन V = ल० × चौ० × ऊँ०
= x(18 – 2x) (18 – 2x)
= x(18 – 2x)x² …(1)
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

प्रश्न 18
45 सेमी लम्बी और 24 सेमी चौड़ी आयताकार लोहे की एक चादर के चारों कोनों से समान भुजा का एक वर्गाकार निकालने के पश्चात् खुला हुआ एक सन्दुक बनाया जाता है। वर्गों की भुजा की माप ज्ञात कीजिये जिसके काटने पर बने सन्दूक का आयतन महत्तम होगा।
उत्तर
माना अभीष्ट वर्ग की भुजा x है तब ।।
सन्दूक की लम्बाई = (45-2x)
तथा सन्दूक की चौड़ाई = (24-2x)
सन्दूक की ऊँचाई = x
∴ सन्दूक का आयतन
V = (45 – 2x) (24 – 2x) x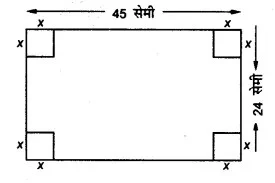


∴x = 5 पर V का मान महत्तम होगा।
∴ वर्ग की भुजा 5 सेमी होगी।

प्रश्न 19.
सिद्ध कीजिए कि एक दिए वृत्त के अन्तर्गत सभी आयतों में वर्ग का क्षेत्रफल उच्चतम होता है।
उत्तर
माना a त्रिज्या के वृत्त के अन्तर्गत आयत की लम्बाई x तथा चौड़ाई y है।
चित्र ABC में,
AC = व्यास = 2a

प्रश्न 20.
सिद्ध कीजिए कि दिए हुए सम्पूर्ण पृष्ठ और महत्तम आयतन के लम्बवृत्तीय बेलन की ऊँचाई , उसके आधार के व्यास के बराबर है।
उत्तर-
माना बेलन की ऊँचाई h तथा आधार की त्रिज्या r है।
पुनः माना बेलन का सम्पूर्ण पृष्ठ S और आयतन V है, तब

प्रश्न 21.
100 सेमी³ आयतन वाले डिब्बे सभी बेलनाकार (लम्ब वृत्तीय) डिब्बों में से न्यूनतम पृष्ठ क्षेत्रफल वाले डिब्बे की विमाएँ ज्ञात कीजिए।
उत्तर-
माना बेलनाकार डिब्बों की त्रिज्या r और ऊँचाई h है।
आयतन = πr²h = 100 सेमी³

प्रश्न 22.
28 मीटर लम्बे तार के दो टुकड़े करके एक को वर्ग तथा दूसरे को वृत्त के रूप में मोड़ा जाता है। दोनों टुकड़ों की लम्बाई ज्ञात कीजिए यदि उनसे बनी आकृतियों को संयुक्त क्षेत्रफल न्यूनतम है।
उत्तर-
तार की लम्बाई l = 28 मी
माना वर्ग की भुजा x तथा वृत्त की त्रिज्या r है, तब
l = वर्ग का परिमाप + वृत्त की परिधि = 4x + 2πr = 28 …(1)
माना संयुक्त क्षेत्रफल A है।
A = वर्ग की क्षेत्रफल + वृत्त का क्षेत्रफल = x² + πr²

प्रश्न 23.
सिद्ध कीजिए कि R त्रिज्या के गोले के अन्तर्गत विशालतम शंकु का आयतन गोले के आयतन का होता है।
उत्तर-
माना V, AB गोले के अन्तर्गत विशालतम शंकु का आयतन है। स्पष्टतया अधिकतम आयतन के लिए शंकु का अक्ष गोले की ऊँचाई के साथ होना चाहिए।
माना ∠AOC = θ,
∴ AC, शंकु के आधार की त्रिज्या = R sin θ, जहाँ R गोले की त्रिज्या है।

प्रश्न 24.
दर्शाइये कि एक निश्चित आयतन के शंक्वाकार डेरे के बनाने में कम-से-कम कपड़ा लगेगा जब उसकी ऊँचाई आधार की त्रिज्या के √2 गुना होगी।
उत्तर-
माना शंकु की ऊँचाई h, त्रिज्या r तथा तिरछी ऊँचाई l है।

प्रश्न 25.
सिद्ध कीजिए कि दी हुई तिर्यक ऊँचाई और महत्तम आयतन वाले शंकु का अर्द्ध शीर्ष कोण tan^-1√2 होता है।
उत्तर-
माना शंकु की त्रिज्या = r, अर्द्धशीर्ष ∠BAM = θ
ऊँचाई = h; तिर्यक ऊँचाई = l
ऊर्ध्वाधर ऊँचाई, h = AM = l cos θ
शंकु की त्रिज्या, r = MC = l sin θ

प्रश्न 26.
सिद्ध कीजिए कि दिए हुए पृष्ठ और महत्त्म आयतन वाले लम्बवृत्तीय शंकु का अर्द्धशीर्ष कोण होता है।
उत्तर-
माना शंकु की त्रिज्या r, तिरछी ऊँचाई l सम्पूर्ण पृष्ठ S तथा आयतन V है।
सम्पूर्ण पृष्ठ S = πr (r + l) या πrl = S – πr²

प्रश्न 27.
वक्र x² = 2y पर (0, 5) से न्यूनतम दूरी पर स्थित बिन्दु है
(A) (2√2, 4)
(B) ( 2√2 , 0)
(C) (0, 0)
(D) (2, 2)
उत्तर-
माना वक्र x² = 2y पर कोई बिन्दु P(x, y) है।
दिया हुआ बिन्दु A (0, 5) है।
PA² = (x – 0)² + (y – 5)² = z (माना)
Z = x² + (y – 5)² …(1)
तथा वक्र x² = 2y …(2)
x² का मान समी० (1) में रखने पर,
Z = 2y + (y – 5)² =2y + y² + 25 – 10y = y² + 25 – 8y
दोनों पक्षों का y के सापेक्ष अवकलन करने पर, 
उच्चतम व निम्नतम मान के लिए, 

प्रश्न 28.
x के सभी वास्तविक मानों के लिए!
का न्यूनतम मान है–
(A) 0
(B) 1
(C) 3
(D) 
उत्तर-

प्रश्न 29.
[x (x – 1) + 1]^1/3,0≤x≤1 का उच्चतम मान है
(A) 
(B) 
(C) 1
(D) 0
उत्तर-
माना y = [x (x – 1) + 1]^1/3
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,


उच्चतम मान = 1
अत: विकल्प (C) सही है।

एनसीईआरटी सोलूशन्स क्लास 12 गणित-I पीडीएफ

• Chapter 1 (सम्बन्ध एवं फलन)
• Chapter 2 (प्रतिलोम त्रिकोणमितीय फलन)
• Chapter 3 (आव्यूह)
• Chapter 4 (सारणिक)
• Chapter 5 (सांतत्य तथा अवकलनीयता)