NCERT Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)

NCERT Solutions Class 12 गणित-II 12 वीं कक्षा से Chapter-13 (प्रायिकता) के उत्तर मिलेंगे। यह अध्याय आपको मूल बातें सीखने में मदद करेगा और आपको इस अध्याय से अपनी परीक्षा में कम से कम एक प्रश्न की उम्मीद करनी चाहिए।

हमने NCERT बोर्ड की टेक्सटबुक्स हिंदी गणित-II के सभी Questions के जवाब बड़ी ही आसान भाषा में दिए हैं जिनको समझना और याद करना Students के लिए बहुत आसान रहेगा जिस से आप अपनी परीक्षा में अच्छे नंबर से पास हो सके।

एनसीईआरटी प्रश्न-उत्तर

Class 12 गणित-II

पाठ-13 (प्रायिकता)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

Exercise 13.1

प्रश्न 1.
यदि E और F इस प्रकार की घटनाएँ हैं कि P (E) = 0.6, P (F) = 0.3 और P(E ∩ F) = 02, तो $Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)$ और ज्ञात कीजिए।
उत्तर
दिया है, P(E) = 0.6, P(F) = 0.3
और P (E ∩ F) = 0.2

प्रश्न 2:
P(A | B) ज्ञात कीजिए यदि P(B) = 0.5 और P(A ∩ B) = 0.32
उत्तर

प्रश्न 3.
यदि P (A) = 0.8, P(B) = 0.5 और 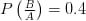तो ज्ञात कीजिए
(i) P(A ∩ B)
(ii) Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)
(iii) P(AU B)
उत्तर
दिया है, P(A) = 0.8, P(B) = 0.5 और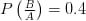

(iii) ∵ P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.8 + 0.5 – 0.32
= 1.3 – 0.32
= 0.98

प्रश्न 4:
P(A ∪ B) ज्ञात कीजिए यदि 2P(A) = P(B) = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) और P(A| B) =
उत्तर

प्रश्न 5:
यदि P(A) = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) ,P(B) = और P(A∪ B) = तो ज्ञात कीजिए
(i) P(A ∩B)
(ii) P(A | B)
(iii) P(B | A)
उत्तर
(i) ∵ P(A ∪ B) = P(A) + P(B) – P(A ∩ B)

• निम्नलिखित प्रश्न 6 से 9 तक ज्ञात कीजिए।

प्रश्न 6.
एक सिक्के को तीन बार उछाला गया है
(i) E : तीसरी उछाल पर चित F : पहली दोनों उछालों पर चित
(ii) E : न्यूनतम दो चित F : अधिकतम एक चित ।
(iii) E : अधिकतम दो पट F : न्यूनतम एक पट
उत्तर
(i) सिक्के को तीन बार उछालने पर कुल प्रतिदर्श समष्टि (प्रकार) = 2³ = 8 समसंभाव्य प्रतिदर्श बिन्दुओं का समुच्चय है जो निम्न प्रकार है।
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
E = तीसरी उछाल पर चित = {HHH, HTH, THH, TTH}

प्रश्न 7.
दो सिक्कों को एक बार उछाला गया है-
(i) E : एक सिक्के पर पट प्रकट होता है F : एक सिक्के पर चित प्रकट होता है।
(ii) E : कोई पट प्रकट नहीं होता है F : कोई चित प्रकट नहीं होता है।
उत्तर
(i) E = एक सिक्के पर पट प्रकट होता है। = {TH, HT}
F = एक सिक्के पर चित प्रकट होता है।
= {HT, TH}
∴ E ∩ F = {TH, HT}
दो सिक्कों को उछालने पर प्रतिदर्श समष्टि = 2² = 4

प्रश्न 8.
एक पासे को तीन बार उछाला गया है
E : तीसरी उछाल पर संख्या 4 प्रकट होना
F : पहली दो उछालों पर क्रमशः 6 तथा 5 प्रकट होना।
उत्तर
E = तीसरी उछाल पर संख्या 4 प्रकट होना तथा F पहली दो उछालों पर क्रमश: 6 तथा 5 प्रकार होना
= (1,1, 4), (1, 2, 4), (1, 3, 4), … (1, 6, 4)
= (2, 1, 4), (2, 2, 4), (2, 3, 4), … (2, 6, 4)
= (3, 1, 4), (3, 2, 4), (3, 3, 4), … (3, 6, 4)
= (4,1, 4), (4, 2, 4), (4, 3, 4), … (4,6, 4)
= (5, 1, 4), (5, 2, 4), (5, 3, 4), … (5, 6, 4)
= (6,1, 4), (6, 2, 4), 6, 3, 4),… (6, 6, 4)
= 36 परिणाम
तथा F = {6, 5, 1), (6, 5, 2), (6, 5, 3), (6, 5, 4), (6, 5, 5), (6, 5, 6)} = 6 परिणाम
∴E ∩ F = {6, 5, 4}

प्रश्न 9.
एक पारिवारिक चित्र में माता, पिता व पुत्र यादृच्छया खड़े हैं
E : पुत्र एक सिरे पर खड़ा है
F : पिता मध्य में खड़े हैं।
उत्तर
यदि एक पारिवारिक चित्र में (m), पिता (f) व पुत्र (s) यादृच्छया खड़े हैं।
कुल तरीके = 3. 2. 1 = 6
E = पुत्र एक सिरे पर खड़ा है।
= {(s m f), (s f m), (f m s), (m f s)}
F = पिता मध्य में खड़े हैं।
= {(m f s), (s f m)}
E ∩ F = {(m f s), (s f m)}

प्रश्न 10.
एक काले और एक लाल पासे को उछाला गया है
(a) पासों पर प्राप्त संख्याओं का योग 9 से अधिक होने की सप्रतिबन्ध प्रायिकता ज्ञात कीजिए यदि यह ज्ञात हो कि काले पासे पर 5 प्रकट हुआ है।
(b) पासों पर प्राप्त संख्याओं का योग 8 होने की सप्रतिबन्ध प्रायिकता ज्ञात कीजिए यदि यह ज्ञात हो कि लाल पासे पर प्रकट संख्या 4 से कम है।
उत्तर
(a) माना A पासों पर प्राप्त संख्याओं को योगफल 9 से अधिक होने की घटना तथा F काले पासे पर 5 प्रकट होने की घटना को निरूपित करता है।
∴ A = {(4, 6), (5, 5), (6,4), (5, 6), (6, 5), (6, 6)}
तथा B = {(5, 1), (5, 2), (5, 3), (5,4), (5, 5), (5, 6)}
∴ A ∩ B = {(5, 5), (5, 6)}
तथा 2 पासों की उछाल में कुल परिणाम = 36

(b) माना A घटना पासों पर प्राप्त संख्याओं का योगफल 8 होने तथा B घटना लाल पासे पर प्रकट संख्या 4 से कम घटित होने को निरूपित करते हैं।
A = {(2, 6), (3, 5), 4, 4), (5, 3), (6, 2)}
B = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), 2, 3), (2,4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), 3, 4), 3, 5), (3, 6)}
कुल प्रकार = 18

प्रश्न 11.
एक सम पाँसे को उछाला गया है। घटनाओं E = {1, 3, 5}, F = {2, 3} और G = {2, 3, 4,5} के लिए निम्नलिखित ज्ञात कीजिए।
(i) P(E | F) और P(F | E)
(ii) P(E | G) और P(G | E)
(iii) P(E ∪ F|G) और P(E ∩ F | G)
उत्तर
प्रश्नानुसार, n(E) = 3, n(F) = 2, n(G) = 4
तथा n(E ∩ F) = 1, n(E ∩ G) = 2
(E ∪ F) = {1, 2, 3, 5}, (E OF) = {3}
⇒ n(E∪F) = 4, n(E OF) =1
∴ (E ∪ F) 2G = {2, 3, 5}, E 0 F G = {3}

प्रश्न 12.
मान लें कि जन्म लेने वाले बच्चे को लड़का या लड़की होना समसंभाव्य है। यदि किसी परिवार में दो बच्चे हैं तो दोनों बच्चों के लड़की होने की सप्रतिबन्ध प्रायिकता क्या है, यदि यह दिया गया है कि
(i) सबसे छोटा बच्चा लड़की है
(ii) न्यूनतम एक बच्चा लड़की है।
उत्तर
माना पहले तथा-दूसरे बच्चे, लड़कियाँ G1, G2 तथा लड़के B1, B2 हैं।
∴ S = { (G1, G2), (G1, B2), (G2, B1), (B1, B2)}
माना A = दोनों बच्चे लड़कियाँ हैं = {G1 G2}
B = सबसे छोटा बच्चा लड़की है = {G1G2, B1G2}
C = न्यूनतम एक बच्चा लड़की है = {G1B2, G1G2, B1G2}
A ∩ B = {G1G2}, A ∩C = {G1G2}

प्रश्न 13:
एक प्रशिक्षक के पास 300 सत्य/असत्य प्रकार के आसान प्रश्न, 200 सत्य/असत्य प्रकार के कठिन प्रश्न, 500 बहुविकल्पीय प्रकार के आसान प्रश्न और 400 बहुविकल्पीय प्रकार के कठिन प्रश्नों का संग्रह है। यदि प्रश्नों के संग्रह से एक प्रश्न यदृच्छया चुना जाता है, तो एक आसान प्रश्न की बहुविकल्पीय होने की प्रायिकता ज्ञात कीजिए।
उत्तर
माना E = आसान प्रश्न पूछे जाने की घटना
तथा F = बहुविकल्पीय प्रश्न पूछे जाने की घटना
तब n(E) = 300 + 500 = 800, n(F) = 500 + 400 = 900
तथा n(E ) F) = 500
∴ अभीष्ट घटना की प्रायिकता = p(F | E) = = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) =

प्रश्न 14.
यह दिया गया है कि दो पासों को फेंकने पर प्राप्त संख्याएँ भिन्न-भिन्न हैं। दोनों संख्याओं का योग 4 होने की प्रायिकता ज्ञात कीजिए।
उत्तर
दो पासों को फेंकने से प्रतिदर्श समष्टि के परिणाम = 6 x 6 = 36
माना A = दो संख्याओं का योग 4 = {(1,3), (2, 2), (3, 1}}
दो पासों को फेंकने पर समान संख्या वाले परिणाम ।
= {(1, 1), (2, 2), (3, 3), 4, 4), (5, 5), 6, 6)} कुल 6 हैं।
∴B = जब संख्या भिन्न हो तो ऐसे परिणाम = 36 – 6 ≠ 30
A ∩ B = {(1, 3), (3, 1)}

प्रश्न 15.
एक पासे को फेंकने के परीक्षण पर विचार कीजिए। यदि पासे पर प्रकट संख्या 3 का गुणज है तो पासे को पुनः फेंकें और यदि कोई अन्य संख्या प्रकट हो तो एक सिक्के को उछालें। घटना न्यूनतम एक पासे पर संख्या 3 प्रकट होना’ दिया गया है तो घटना ‘सिक्के पर पट प्रकट होने की सप्रतिबन्ध प्रायिकता ज्ञात कीजिए।
उत्तर
दिए गए परीक्षण के परिणामों को निम्न समुच्चय के द्वारा प्रदर्शित करते हैं।

∴ n(S) = 20
माना घटना E सिक्के पर पट प्रकट होना तथा घटना F न्यूनतम एक पासे पर संख्या 3 प्रकट होना को निरूपित करते हैं।
E = [(1, T), (2, T), (4, T), (5, T)] ⇒ n (E) = 4
F = [(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (6, 3)]
n(F) = 7
E ∩ F = 0 क्योंकि कोई उभयनिष्ठ बिन्दु नहीं है।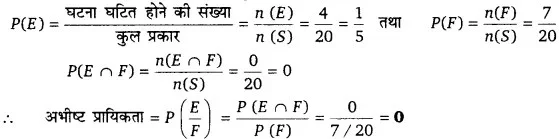

• निम्नलिखित प्रश्नों में से प्रत्येक में सही उत्तर चुनें।

प्रश्न 16.

उत्तर

प्रश्न 17.

उत्तर

Exercise 13.2

प्रश्न 1:
यदि P(A)= $Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)$ और P(B) = A व B स्वतन्त्र घटनायें हैं, तो P(A ∩ B) ज्ञात कीजिए।
उत्तर
∵ A व B स्वतन्त्र घटनाये हैं।
∴ P(A ∩ B) = P(A) . P(B) = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) x =

प्रश्न 2.
52 पत्तों की एक गड्डी में से यदृच्छया बिना प्रतिस्थापित किये दो पत्ते निकाले गए। दोनों पत्तों के काले रंग का होने की प्रायिकता ज्ञात कीजिए।
उत्तर
ताश की गड्डी में 26 काले पत्ते होते हैं।
आगे उपरोक्त प्रश्न की भाँति हल करें।

प्रश्न 3.
सन्तरों के एक डिब्बे का निरीक्षण उसमें से तीस सन्तरों को यदृच्छया बिना प्रतिस्थापित किये हुए निकाल कर किया जाता है। यदि तीनों निकाले गये सन्तरें अच्छे हैं; तो डिब्बे को बिक्री के लिए स्वीकृत किया जाता है अन्यथा अस्वीकृत कर देते हैं। एक डिब्बा जिसमें 15 सन्तरें हैं जिनमें से 12 अच्छे व ३ खराब सन्तरें हैं, के बिक्री के लिए स्वीकृत होने की प्रायिकता ज्ञात कीजिए।
उत्तर
माना पहली, दूसरी व तीसरी निकाल में अच्छा सन्तरा निकलने की घटनायें क्रमश: A, B व C है।
तब अभीष्ट प्रायिकता = P(A ∩ B ∩ C)
अब P(A) = पहली निकाल में अच्छा सन्तरा निकलने की प्रायिकता = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) x
पहली निकाल में एक अच्छा सन्तरा निकलने के बाद शेष सन्तरों की संख्या 14 है जिसमें 11 सन्तरे अच्छे हैं।
∴ P(B | A) = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)
दूसरी निकाल में भी एक अच्छा सन्तरा निकलने के बाद शेष सन्तरे 13 हैं जिसमें 10 सन्तरे अच्छे हैं।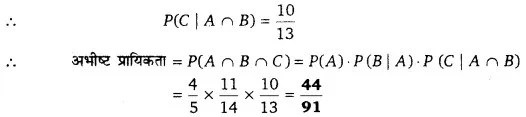

प्रश्न 4.
एक न्याय्य सिक्का और एक अभिनत पाँसे को उछाला गया। माना A घटना ‘सिक्के पर चित प्रकट होता है और B घटना पाँसे पर संख्या 3 प्रकट होती है’ को निरूपित करते हैं। निरीक्षण कीजिए कि घटनाएँ स्वतन्त्र हैं या नहीं ?
उत्तर
इस प्रयोग की प्रतिदर्श समष्टि इस प्रकार होगी
S = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, 1),(T, 2), (T, 3), (T, 4), T, 5), (T, 6)}
A = सिक्के पर चित प्रकट होना; B = पाँसे पर संख्या 3 प्रकट होती है।
(A ∩ B) = {(H, 3}}
तब n(S) = 12, n(A) = 6, n(B) = 2
तथा n(A ∩ B) = 1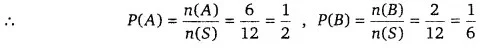

प्रश्न 5.
एक पाँसे पर 1, 2, 3 लाल रंग से और 4, 5, 6 हरे रंग से लिखे गए हैं। इस पाँसे को उछाला गया। माना A घटना संख्या सम है’ और B घटना ‘संख्या लाल रंग से लिखी गई है’ को निरूपित करते हैं। क्या A और B स्वतन्त्र हैं?
उत्तर
इस प्रयोग की प्रतिदर्श समष्टि S = {1, 2, 3, 4, 5, 6} ⇒ n(S) = 6
घटना A = {2, 4, 6} } ⇒ n(A) = 3
तथा घटना B = {1, 2, 3} ⇒ n(B) = 3
तब (A ∩ B) = {2} ⇒ n(A ∩ B) = 1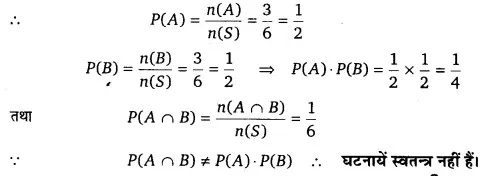

प्रश्न 6.
माना E तथा F दो घटनाएँ इस प्रकार हैं कि P(E) = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) , P(F) = और P(E ∩ F) = तब क्या E तथा F स्वतन्त्र हैं?
उत्तर
∵ P(E). P(F) = x = ≠ P(E ∩ F)
∴ घटनायें स्वतन्त्र नहीं हैं।

प्रश्न 7.
A और B ऐसी घटनाएँ दी गई हैं जहाँ P(A) = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) ,P(A ∪ B) = तथा P(B) = p, तो p का मान ज्ञात कीजिए यदि (i) घटनाएँ परस्पर अपवर्जी हैं, (ii) घटनाएँ स्वतन्त्र हैं।
उत्तर
(i) चूँकि घटनायें परस्पर अपवर्जी हैं।
∴ P(A ∩ B) = 0
पुन: P(A ∪ B) = P(A) + P(B) – P(A ∩ B)

प्रश्न 8:
माना A और B स्वतन्त्र घटनायें है तथा P(A) = 0.3 और P(B) = 0.4 तब
(i) P (A ∩ B)
(i) P(A ∪ B)
(iii) P(A| B)
(iv) P(B | A) ज्ञात कीजिए।
उत्तर
(i) ∵ A व B स्वतन्त्र घटनायें हैं।
∴ P(A ∩ B) = P(A): P(B) = 0.3 x 0.4 = 0.12
(ii) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.3 + 0.4 – 0.12 = 0.58

प्रश्न 9.
दी गई घटनाएँ A और B ऐसी हैं, जहाँ P(A) = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) ,P(B) = और P(A ∩ B) = तब P(A- नहीं और B -नहीं) ज्ञात कीजिए।
उत्तर

प्रश्न 10:
माना A और B दो घटनाएँ हैं और P(A) = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) तथा P(B) = और P(A- नहीं और B-नहीं)= , क्या A और B स्वतन्त्र घटनायें हैं?
उत्तर

प्रश्न 11:
A और B स्वतन्त्र घटनाएँ दी गई हैं जहाँ P(A) = 0.3, P(B) = 0.6 तो
(i) P(A और B)
(ii) P(A और B – नहीं)
(iii) P(A या B)
(iv) P(A और B में कोई भी नहीं) का मान ज्ञात कीजिए।
उत्तर
(i) P(A और B) = P(A ∩ B) = P(A): P(B) ∵ P(A) व P(B) स्वतन्त्र घटनायें हैं।
= 0.3 x 0.6 = 0.18

(ii) P(A और B -नहीं) = P(A ∩ $Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)$ ) = P(A): P( $Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)$ )
= P(A): [1 – P(B)]
= 0.3 [1 – 0.6] = 0.3 x 0.4 = 0.12

(iii) P(A या B) = P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.3 + 0.6 – 0.18 = 0.72

(iv) P(A और B में कोई भी नहीं) = P( $Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)$ ∩ $Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)$ )
= P() = 1 – P(A ∪ B)
= 1 – 0.72 = 0.28

प्रश्न 12.
एक पाँसे को तीन बार उछाला जाता है कम से कम एक बार विषम संख्या प्राप्त होने की प्राकियता ज्ञात कीजिए।
उत्तर
पाँसे की पहली उछाल में कुल अंक प्राप्त होने की स्थिति = 6
तथा विषम अंक प्राप्त न होने की स्थिति = 3
∴ पहले उछाल में विषम अंक प्राप्त न होने की प्रायिकता P(A) = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) =
इसी प्रकार दूसरे उछाल में विषम अंक प्राप्त न होने की प्रायिकता P(B) =
तीसरे उछाल में विषम अंक प्राप्त न होने की प्रायिकता P(C) = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)
∵ उपरोक्त तीनों घटनायें स्वतन्त्र हैं।
∴ तीनों के एक साथ घटने की प्रायिकता अर्थात् प्रत्येक उछाल में विषम संख्या प्राप्त न होने की घटना

प्रश्न 13.
दो गेंदें एक बॉक्स से बिना प्रतिस्थापित किये निकाली जाती हैं। बॉक्स में 10 काली और 8 लाल गेंदें हैं तो प्रायिकता ज्ञात कीजिए।
(i) दोनों गेंदें लाल हों।
(ii) प्रथम काली एवं दूसरी लाल हो।
(iii) एक काली तथा दूसरी लाल हो।
उत्तर
माना R = लाल गेंद निकलने की घटना; B = काली गेंद निकलने की घटना
(i) पहले निकाल में लाल गेंद निकलने की प्रायिकता P(R) = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) = =
क्योंकि गेंद पुनः वापस डाल दी जाती है।
∴ दूसरे निकाल में लाल गेंद निकलने की प्रायिकता P(R) =
∴ दोनों गेंद लाल निकलने की प्रायिकता = P(R). P(R) =

(ii) पहले निकाल में काली गेंद निकलने की प्रायिकता P(B) = =
दूसरे निकाल में लाल गेंद निकलने की प्रायिकता P(R) =
∴ P(पहली काली और दूसरी लाल) = P(B). P(R) = $Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)$ x =

(iii) P(एक काली और एक लाल) = P(प्रथम काली और दूसरी लाल) +P(प्रथम लाल और दूसरी काली)
= Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) . + .=

प्रश्न 14.
एक विशेष प्रश्न को A और B द्वारा स्वतन्त्र रूप से हल करने की प्रायिकताएँ क्रमशः $Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)$ और $Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)$ हैं। यदि दोनों स्वतन्त्र रूप से समस्या हल करने का प्रयास करते हैं, तो प्रायिकता ज्ञात कीजिए कि
(i) प्रश्ल हल हो जाता है।
(ii) उनमें से तथ्यतः कोई एक प्रश्न हल कर लेता है।
उत्तर

प्रश्न 15.
ताश के 52 पत्तों की एक ठीक से फैटी गई गड्डी से एक पत्ता यदृच्छया निकाला जाता है। निम्नलिखित में से किन दशाओं में घटनाएँ E और F स्वतन्त्र हैं?
(i) E : ‘निकाला गया पत्ता हुकुम का है
F : ‘निकाला गया पत्ता इक्का है ।

(ii) E : निकाला गया पत्ता काले रंग का है।
F : निकाला गया पत्ता एक बादशाह है।

(iii) E : निकाला गया पत्ता एक बादशाह या एक बेगम है।
F : निकाला गया पत्ता एक बेगम या एक गुलाम है।
उत्तर
(i) E : निकाला गया पत्ता हुकुम का है।

(ii) E : निकाला गया पत्ता काले रंग का है।

(iii) E: निकाला गया पत्ता एक बादशाह या एक बेगम है।

प्रश्न 16.
एक छात्रावास में 60% विद्यार्थी हिंदी का, 40% अंग्रेजी का और 20% दोनों अखबार पढ़ते हैं। एक छात्रा को यदृच्छया चुना जाता है।
(a) प्रायिकता ज्ञात कीजिए कि वह न तो हिंदी और न ही अंग्रेजी का अखबार पढ़ती है।
(b) यदि वह हिंदी का अखबार पढ़ती है तो उसके अंग्रेजी का अखबार भी पढ़ने वाली होने की प्रायिकता ज्ञात कीजिए।
(c) यदि वह अंग्रेजी का अखबार पढ़ती है तो उसके हिंदी का अखबार भी पढ़ने वाली होने की प्रायिकता ज्ञात कीजिए।
उत्तर
माना H = हिंदी का अखबार पढ़ने की घटना; E = अंग्रेजी का अखबार पढ़ने की घटना

प्रश्न 17.

उत्तर

प्रश्न 18.

उत्तर

Exercise 13.3

प्रश्न 1.
एक कलश में 5 लाल और 5 काली गेंदें हैं। यादृच्छया एक गेंद निकाली जाती है, इसका रंग नोट करने के बाद पुनः कलश में रख दी जाती है। पुनः निकाले गएं रंग की 2 अतिरिक्त गेंदें कलश में रख दी जाती हैं तथा कलश में से एक गेंद निकाली जाती है दूसरी गेंद की लाल होने की प्रायिकता क्या है?
उत्तर
क्योंकि एक कलश में 5 लाल और 5 काली गेंदें हैं।
(i) माना एक लाल गेंद निकाली जाती है।
∴ कुल 10 गेंदों में से एक लाल गेंद निकालने की प्रायिकता = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) .
अब यदि दो लाल गेंदें कलश में रख दी जाती हैं।
कलश में 7 लाल और 5 काली गेंदें हैं।
लाल गेंद निकालने की प्रायिकता = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)

(ii) माना पहले काली गेंद निकाली जाती है।
कुल 10 गेंदों में से एक काली गेंद निकालने की प्रायिकता = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) .
फिर दो काली गेंदें कलश में रख दी जाती हैं।
अब कलश में 5 लाल और 7 काली गेंदें हैं।
एक लाल गेंद होने की प्रायिकता = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)
दूसरी लाल गेंद होने की प्रायिकता =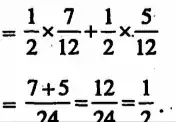

प्रश्न 2.
एक थैले में 4 लाल और 4 काली गेंदें हैं और एक अन्य थैले में 2 लाल और 6 काली गेंदें हैं। दोनों थैलों में से एक को यदृच्छया चुना जाता है और उसमें से एक गेंद निकाली जाती है जो कि लाल है। इस बात की प्रायिकता ज्ञात कीजिए कि गेंद पहले थैले से निकाली गयी है।
उत्तर
माना पहले वे दूसरे थैले को चुनने की घटनायें क्रमश: E₁ व E₂ हैं, तब

प्रश्न 3.
छात्रों में से एक कॉलेज में, यह ज्ञात है कि 60% छात्रावास में रहते हैं और 40% दिन विद्वान हैं (छात्रावास में नहीं रहते हैं)। पिछले साल के परिणाम रिपोर्ट करते हैं कि छात्रावास में रहने वाले सभी छात्रों में से 30% एक ग्रेड प्राप्त करते हैं और दिन के 20% विद्वान अपनी वार्षिक परीक्षा में एक ग्रेड प्राप्त करते हैं। वर्ष के अंत में, एक छात्र को कॉलेज से यादृच्छिक रूप से चुना जाता है और उसके पास ए-ग्रेड होता है क्या छात्र संभावना है कि छात्र एक होस्टल हो?
उत्तर
E1, E2 और ए निम्नलिखित का प्रतिनिधित्व करते हैं:
E1 = हॉस्टल में रहने वाले छात्र,
E2 दिन विद्वान (छात्रावास में नहीं रह रहे हैं)
और A = छात्र जो ग्रेड A प्राप्त करते हैं

प्रश्न 4.
एक बहुविकल्पीय प्रश्न का उतर देने में एक विद्यार्थी या तो प्रश्न का उत्तर जानता है या वह अनुमान लगाता है। माना कि उसके उत्तर जानने की प्रायिकता Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) है और अनुमान लगाने की प्रायिकता है। मान लें कि छात्र के प्रश्न के उत्तर का अनुमान लगाने पर सही उत्तर देने की प्रायिकता Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) है तो इस बात की प्रायिकता क्या है कि कोई छात्र प्रश्न का उत्तर जानता है यदि यह ज्ञात है कि उसने सही उत्तर दिया है?
उत्तर
माना E₁ : विद्यार्थी उत्तर जानता है; E₂ : विद्यार्थी अनुमान लगाता हो।
E: विद्यार्थी सही उत्तर देता है।

प्रश्न 5.
किसी विशेष रोग के सही निदान के लिए रक्त की जाँच 99% असरदार है, जब वास्तव में रोगी उस रोग से ग्रस्त होता है। किंतु 0.5% बार किसी स्वस्थ व्यक्ति की रक्त जाँच करने पर निदान गलत रिपोर्ट देता है यानी व्यक्ति को रोग से ग्रस्त बतलाता है। यदि किसी जनसमुदाय में 0.1% लोग उस रोग से ग्रस्त हैं तो क्या प्रायिकता है कि कोई यदृच्छया चुना गया व्यक्ति उस रोग से ग्रस्त होगा यदि उसके रक्त की जाँच में ये बताया जाता है कि उसे यह रोग है?
उत्तर
माना E₁ : एक व्यक्ति को विशेष रोग होना;
E₂ : एक व्यक्ति को विशेष रोग न होना।
तथा E : घटना जब जाँच की रिपोर्ट पॉजीटिव है।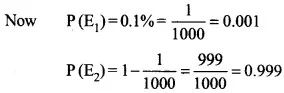

प्रश्न 6.
तीन सिक्के दिए गए हैं। एक सिक्के के दोनों ओर चित्त ही है। दूसरा सिक्का अभिनत (biased) है जिसमें चित्त 75% बार प्रकट होता है और तीसरा अनभिनत सिक्का है। तीनों में से एक सिक्के को यदृच्छयो चुना गया और उसे उछाला गया है। यदि सिक्के पर चित्त प्रकट हो, तो क्या
प्रायिकता है कि वह दोनों चित्त वाला सिक्का है?
उत्तर
E₁ : सिक्का जिसमें दोनों तरफ चित्त है, चुने जाने की घटना।
E₂ : अभिनत सिक्का जिसमें चित्त 75% प्रकट होता है, चुने जाने की घटना
E₃ : अनभिनत सिक्का चुने जाने की घटना
E : सिक्के पर चित्त प्रकट होने की घटना
प्रश्नानुसार,

प्रश्न 7.
एक बीमा कम्पनी 2000 स्कुटर चालकों, 4000 कार चालकों और 6000 ट्रक चालकों का बीमा करती है। दुर्घटनाओं की प्रायिकताएँ क्रमशः 0.01, 0.03 और 0.15 है। बीमाकृत व्यक्तियों ( चालकों ) में से एक दुर्घटना ग्रस्त हो जाता है। उस व्यक्ति के स्कूटर चालक होने की प्रायिकता ज्ञात कीजिए।
उत्तर
माना E₁ : बीमित व्यक्ति एक स्कूटर चालक है; E₂ : बीमित व्यक्ति एक कार चालक है।
E₃ : बीमित व्यक्ति एक ट्रक चालक है; E : बीमित व्यक्ति दुर्घटना ग्रस्त है।

प्रश्न 8.
एक कारखाने में A और B दो मशीनें लगी हैं। रिकार्ड से ज्ञात होता है कि कुल उत्पादन का 60% मशीन A और 40% मशीन B द्वारा किया जाता है। इसके अतिरिक्त मशीन A का 2% और मशीन B का 1% उत्पादन खराब है। यदि कुल उत्पादन का एक ढेर बना लिया जाता है और उसे ढेर से यदृच्छया निकाली गई वस्तु खराब हो तो इस वस्तु के मशीन A द्वारा बने होने की प्रायिकता ज्ञात कीजिए।
उत्तर
माना कि घटनायें E₁ व E₂ इस प्रकार हैं।
E₁ = वस्तु मशीन A द्वारा बनायी गयी है; E₂ = वस्तु मशीन B द्वारा बनायी गयी है। E = वस्तु खराब है।
तब प्रश्नानुसार, P(E₁) = 0.6, P(E₂) = 0.4
P(E | E₁ ) = वस्तु के खराब होने की प्रायिकता जबकि वह मशीन A द्वारा बनायी गयी है।
= Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) = 0.02
इसी प्रकार P(E | E₂) = = 0.01
अब वस्तु के मशीन A द्वारा बने होने की प्रायिकता जबकि वह खराब है = P(E₁ | E)

प्रश्न 9.
दो समूह निगम के निदेशक मंडल की स्थिति के लिए प्रतिस्पर्धा कर रहे हैं। संभावनाएं जो पहले और दूसरे समूह जीतेंगे क्रमश: 0.6 और 0.4 हैं। इसके अलावा, यदि पहला समूह जीतता है, तो एक नया उत्पाद पेश करने की संभावना 0.7 है और दूसरा समूह जीतने पर संबंधित संभावना 0.3 है। संभावना है कि नए उत्पाद को पेश किया गया नया उत्पाद दूसरे समूह द्वारा किया गया था।
उत्तर
दिया गया: P (G1) = 0.6, P (G2) = 0.4
P नए उत्पाद P (P | G1) = 0.7 और P (P | G2) = 0.3 के लॉन्चिंग का प्रतिनिधित्व करता है

प्रश्न 10.
कोई लड़की एक पाँसा उछालती है। यदि उसे 5 या 6 की संख्या प्राप्त होती है तो वह एक सिक्के को तीन बार उछालती है और ‘चित्तों की संख्या नोट करती है। यदि उसे 1, 2, 3 या 4 की संख्या प्राप्त होती है तो वह एक सिक्के को एक बार उछालती है और यह नोट करती है कि उस पर चित्त या पट प्राप्त हुआ। यदि उसे ठीक एक चित्त प्राप्त होता है, तो उसके द्वारा उछाले गए पाँसे पर 1, 2, 3 या 4 प्राप्त होने की प्रायिकता क्या है?
उत्तर
माना E₁ = एक पाँसे के उछाल पर संख्या 5 या 6 का आना
E₂= एक पाँसे के उछाल पर संख्या 1, 2, 3 या 4 का आना
E = सिक्के के उछाल में एक ही चित्त का आना

प्रश्न 11.
एक निर्मात्म के पास A, B तथा C मशीन ऑपरेटर है। प्रथम ऑपरेटर A,1% खराब सामग्री उत्पादित करता है तथा ऑपरेटर B और C क्रमशः 5% और 7% खराब सामग्री उत्पादित करते हैं। कार्य पर A कुल समय का 50% लगाता है, B कुल समय का 30% तथा कुले समय का 20% लगाता है। यदि एक खराब सामग्री उत्पादित है तो इसे A द्वारा उत्पादित किए जाने की प्रायिकता क्या है?
उत्तर
माना E₁ : ऑपरेटर A द्वारा उत्पादित होने की घटना
E₂ : ऑपरेटर B द्वारा उत्पादित होने की घटना
E₃ : ऑपरेटर C द्वारा उत्पादित होने की घटना
E : एक खराब सामग्री उत्पादित होने की घटना

प्रश्न 12.
52 ताशों की गड्डी से एक पत्ता खो जाता है। शेष पत्तों से दो पत्ते निकाले जाते हैं जो ईंट के पत्ते हैं। खो गये पत्ते की ईंट होने की प्रायिकता क्या है?
उत्तर
माना E₁ : खोने वाला पत्ता ईंट का है;
E₂ : खोने वाला पत्ता पान का है।
E₃ : खोने वाला पत्ता चिड़ी का है
E₄ : खोने वाला पत्ता हुकम का है।
E : शेष पत्तों से 2 ईंट के पत्ते निकालने की घटना

प्रश्न 13:

उत्तर

प्रश्न 14:

उत्तर

Exercise 13.4

प्रश्न 1:
बताइए कि निम्नलिखित प्रायिकता बंटनों में कौन-से एक यादृच्छिक चर के लिए सम्भव नहीं है। अपना उत्तर कारण सहित लिखिए।

उत्तर
(i) यहाँ पर P(X = 0) + P(X = 1) + P(X = 2) = 0.4 + 0.4 + 0.2 = 1
और सभी P(X) ≥ 0
∴ यह प्रायिकता बंटन सम्भव है।
(ii) यहाँ पर P (X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)
= 0.1 + 0.5 + 0.2-0.1 + 0.3 = 1.0
परन्तु P(X = 3) = -0.1 < 0
∴ यह प्रायिकता बंटन सम्भव नहीं है।
(iii) यहाँ पर, P(Y = – 1) + P{Y = 0) + P(Y = 1)
= 0.6 + 0.1 + 0.2 = 0.9 ≠ 1
∴ यह प्रायिकता बंटन सम्भव नहीं है।
(iv) यहाँ पर, P(Z = 3) + P(Z = 2) + P(Z = 1) + P(2 = 0) + P(Z = -1)
= 0.3 + 0.2 + 0.4 + 0.1 + 0.05 ≠ 1.054 1
∴ यह प्रायिकता बंटन सम्भव नहीं है।

प्रश्न 2:
एक कलश में 5 लाल और 2 काली गेंद हैं। दो गेंद यदृच्छया निकाली गई। मान लीजिए x काली गेंदों की संख्या को व्यक्त करता है। X के सम्भावित मान क्या हैं? क्या X यदृच्छिक चर है ?
उत्तर
हमारे पास 5 लाल और 2 काली गेंदें हैं। जब दो गेंद यदृच्छया निकाली गईं, तब निम्नलिखित सम्भावना बन सकती हैं।
(i) निकाली गई दोनों गेंदें लाल हैं (ii) 1 गेंद लाल, एक काली (iii) दोनों काली
(i) में X = 0 (ii) में X = 1 (iii) में X = 2
∴ परिणाम X = {0, 1, 2}
∵ X का परिसर वास्तविक संख्याओं का समुच्चय है।
इसलिए x एक यादृच्छिक चर है।

प्रश्न 3:
यदि X चित्तों की संख्या और पटों की संख्या में अन्तर को व्यक्त करता है, जबकि एक सिक्के को 6 बार उछाला जाता है। सम्भावित मूल्य क्या हैं?
उत्तर
यदि एक सिक्का 6 बार उछाला गया हो तो, चित्तों व पटों की कुल संख्याएँ = 2⁶ = 64
चित्त व पट इस प्रकार आ सकते हैं।
(i) 6 चित्त, 0 पट
(ii) 5 चित्त, 1 पेट
(iii) 4 चित्त, 2 पट
(iv) 3 चित्त, 3 पट
(v) 2 चित्त, 4 पट
(vi) 1 चित्त, 5 पट
(vii) 0 चित्त, 6 पट
चूँकि X: चित्तों की संख्या और पटों की संख्या में अन्तर को व्यक्त करता है।
इसलिए
(i) में X = 6 – 0= 6
(ii) में X = 5 – 1 = 4
(iii) में X = 4 – 2 = 2
(iv) में X = 3 – 3 = 0
(v) में X = 4 – 2 = 2
(vi) में X = 5 -1 = 4
(vii) में X = 6 – 0 = 6
इसलिए X के सम्भावित मूल्य = 0, 2, 4, 6

प्रश्न 4:
निम्नलिखित के प्रायिकता बंटन ज्ञात कीजिए
(i) एक सिक्के की दो उछालों में चित्तों की संख्या का
(ii) तीन सिक्कों को एक साथ एक बार उछालने पर पटों की संख्या का
(ii) एक सिक्के की चार उछालों में चित्तों की संख्या का
उत्तर
(i) सिक्के की दो उछालों की प्रतिदर्श समष्टि : S = {HH, HT, TH, TT}

प्रश्न 5:
एक पाँसा दो बार उछालने पर सफलता की संख्या का प्रायिकता बंटन ज्ञात कीजिए जहाँ
(i) ‘4 से बड़ी संख्या’ को एक सफलता माना गया है।
(ii) न्यूनतम एक ‘पाँसे पर संख्या 6 प्रकट होना’ को एक सफलता माना गया है।
उत्तर
(i) पॉसे की एक उछाल की प्रतिदर्श समष्टि S = {1, 2, 3, 4, 5, 6}
सफलता की प्रायिकता =P(सफलता)

प्रश्न 6.
30 बल्बों के समूह में, जिसमें 6 खराब हैं, 4 बल्बों का एक नमूना ( प्रतिदर्श ) यदृच्छया बिना प्रतिस्थापन के निकाला जाता है। खराब बल्बों की संख्या का प्रायिकता बंटन ज्ञात कीजिए।
उत्तर
कुल बल्ब = 30
खराब बल्ब = 6, सही बल्ब = 30 – 6 = 24

प्रश्न 7.
एक सिक्का समसर्वय सन्तुलित नहीं है जिसमें चित्त प्रकट होने की सम्भावना पट प्रकट होने की सम्भावना की तीन गुनी है। यदि सिक्का दो बार उछाला जाता है तो पटों की संख्या का प्रायिकता बंटन ज्ञात कीजिए।
उत्तर
क्योंकि चित्त और पट की प्रायिकता का अनुपात 3 : 1 है।

प्रश्न 8.
एक यादृच्छिक चर x का प्रायिकता बंटन नीचे दिया गया है। (NCERT)

ज्ञात कीजिए
(i) k
(ii) P(X < 3)
(iii) P(X > 6)
(iv) P(0<X <3)
उत्तर
(i) चूंकि ∑P(X) = 1
∴ 0+k+ 2k + 2k + 3k + k² + 2k² + 7k² + k = 1
⇒ 10k² + 9k-1 = 0
⇒ (10k – 1) (k + 1) = 0 ⇒ k = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) , -1
क्योंकि P(X) ≥ 0 ∴ k = -1 नहीं हो सकता
अतः k =
P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)
= 0 + k+ 2k = 3k =

प्रश्न 9.
एक यादृच्छिक चर X का प्रायिकता फलन P(x) निम्न प्रकार से है, जहाँ # कोई संख्या है।

(a) k का मान ज्ञात कीजिए।
(b) P(x<2), (x≤2),P(x≥2) ज्ञात कीजिए।
उत्तर
(a) चूंकि किसी यादृच्छिक चर के प्रायिकता बंटन का कुल योग 1 के बराबर होता है।
अर्थात ∑P(X) = 1
अत: P(0) + P(1) + P(2) + P (अन्यथा) = 1
∴ k + 2k + 3k + 0 = 1 या 6k = 1 ∴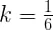
∴ अभीष्ट प्रायिकता बंटन निम्नलिखित है

प्रश्न 10:
एक न्याय्य सिक्के की तीन उछालों पर प्राप्त चित्तों की संख्या का माध्यज्ञात कीजिए।
उत्तर
माना तीन सिक्कों की उछाल में X चित्त आने की संख्या दर्शाता है।
तब X = 0, 1, 2 या 3
अब P(H) = एक सिक्के के उछाल पर चित्त आने की प्रायिकता = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)

प्रश्न 11:
दो पाँसों को युग्मत् उछाला गया। यदि x, छक्कों की संख्या को व्यक्त करता है, तो x की प्रत्याशा ज्ञात कीजिए।
उत्तर
स्पष्ट है कि X = 0, 1, 2
P(X = 0) = किसी भी पासे पर 6 न आने की प्रायिकता = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)
केवल एक पाँसे पर 6 आने की घटना
{(1, 6), (2, 6), (3, 6), (4, 6), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5)}
∴ P(X = 1) = एक 6 आने की प्रायिकता = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)
P(X = 2) = P((6, 6)) =
अत: X का प्रायिकता बंटन है।

प्रश्न 12:
प्रथम छः धन पूर्णाकों में से दो संख्याएँ यदृच्छया ( बिना प्रतिस्थापन ) चुनी गई। मान लें x दोनों संख्याओं में से बड़ी संख्या को व्यक्त करता है। E(X) ज्ञात कीजिए।
उत्तर
स्पष्ट है X का मान 2, 3, 4, 5, 6 हो सकता है।
P(X = 2) = प्रायिकता जब दोनों संख्याओं में बड़ी संख्या 2 है।
⇒ P(X = 2) = P((1, 2) या (2, 1))

प्रश्न 13:
मान लीजिए दो पाँसों को फेंकने पर प्राप्त संख्याओं के योग को x से व्यक्त किया गया है। X का प्रसरण और मानक विचलन ज्ञात कीजिए।
उत्तर
दो पाँसों की फेंक में कुल घटनायें = 6 x 6 = 36
जिन्हें (x_i ;y_i}) के रूप में लिख सकते हैं,
जहाँ x_i = 1, 2, 3, 4, 5, 6, y_i = 1, 2, 3, 4, 5, 6
यादृच्छिक चर X के मान अर्थात् पाँसों पर प्राप्त संख्याओं का योग 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 या 12 हो सकता है।

प्रश्न 14:
एक कक्षा में 15 छात्र हैं जिनकी आयु 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 और 20 वर्ष हैं। एक छात्र को इस प्रकार चुना गया कि प्रत्येक छात्र के चुने जाने की सम्भावना समान है और चुने गए छात्र की आयु (X) को लिखा गया। यादृच्छिक चर x को प्रायिकता बंटन ज्ञात कीजिए। x का माध्य, प्रसरण व मानक विचलन भी ज्ञात कीजिए।
उत्तर
X का प्रायिकता बंटन इस प्रकार होगा (स्वयं ज्ञात कीजिए।)

प्रश्न 15.
एक बैठक में 70% सदस्यों ने किसी प्रस्ताव का अनुमोदन किया और 30% सदस्यों ने विरोध किया। एक सदस्य को यदृच्छया चुना गया और, यदि उसे सदस्य ने प्रस्ताव का विरोध किया हो तो x = 0 लिया गया, जब कि यदि उसने प्रस्ताव का अनुमोदन किया हो तो x = 1 लिया गया। Ex)
और प्रसरण (X) ज्ञात कीजिए।
उत्तर
X का प्रायिकता बंटन इस प्रकार होगा।

• निम्नलिखित में से प्रत्येक में सही उत्तरे चुनें।।

प्रश्न 16.
तीन चेहरे पर 1 लिखा हुआ मरने पर प्राप्त संख्या का मतलब, दो चेहरों पर 2 और एक चेहरे पर 5 है
(a) 1
(b) 2
(c) 5
(d) Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)
उत्तर

Mean 2
विकल्प (b) सही है

प्रश्न 17.
मान लीजिए कि दो कार्ड कार्ड के डेक से यादृच्छिक रूप से खींचे जाते हैं। X को प्राप्त एसेस की संख्या होने दें। E(X) का मूल्य क्या है?
(a) Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)
(b)
(c)
(d)
उत्तर
n(S) = 52, n(A) = 4

अभी व E(X) =
विकल्प (d) सही है

Exercise 13.5

प्रश्न 1:
एक पाँसे को 6 बार उछाला जाता है।
यदि ‘पाँसे पर सम संख्या प्राप्त होना’ एक सफलता है तो निम्नलिखित की प्रायिकता क्या होंगी?
(i) तथ्यतः 5 सफलताएँ
(ii) न्यूनतम 5 सफलताएँ
(iii) अधिकतम 5 सफलताएँ
उत्तर
मानी प्रयोग में सफलता की प्रायिकता = p

प्रश्न 2:
बड़ी मात्रा में वस्तुओं में 5% दोषपूर्ण वस्तुएं हैं। संभावना है कि 10 वस्तुओं के नमूने में एक से अधिक दोषपूर्ण आइटम शामिल नहीं होंगे?
उत्तर
एक दोषपूर्ण वस्तु प्राप्त करने की संभावना = 5%
= Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)
=
एक अच्छी वस्तु प्राप्त करने की संभावना = =
10 आइटम के नमूने में एक से अधिक दोषपूर्ण आइटम शामिल नहीं हैं।
=> नमूना में सबसे अधिक है (मुझे दोषपूर्ण आइटम इसकी संभावना = P (0) + P (1)

प्रश्न 3.
वस्तुओं के एक ढेर में 5% त्रुटियुक्त वस्तुएँ हैं। इसकी क्या प्रायिकता है कि 10 वस्तुओं के एक प्रतिदर्श में एक से अधिक त्रुटियुक्त वस्तुएँ नहीं होंगी?
उत्तर
एक त्रुटियुक्त वस्तु प्राप्त होने की प्रायिकता p = 5 % = $Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)$ = $Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)$
एक अच्छी वस्तु प्राप्त होने की प्रायिकता q = $Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)$ = $Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)$
10 वस्तुओं के एक प्रतिदर्श में एक से अधिक त्रुटियुक्त वस्तुएँ नहीं होंगी।

प्रश्न 4.
पासा की एक जोड़ी 4 बार फेंक दिया जाता है। यदि डबलेट प्राप्त करना सफल माना जाता है, तो दो सफलताओं की संभावनाएं पाएं।
उत्तर
n(S) = 36, A = {11,22,33,44,55,66}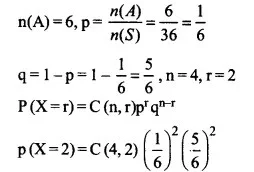

प्रश्न 5.
किसी फैक्ट्री में बने एक बल्ब की 150 दिनों के उपयोग के बाद फ्यूज होने की प्रायिकता 0.05 है। इसकी प्रायिकता ज्ञात कीजिए कि इस प्रकार के 5 बल्बों में से
(i) एक भी नहीं
(ii) एक से अधिक नहीं
(iii) एक से अधिक
(iv) कम-से-कम एक, 150 दिनों के उपयोग के बाद फ्यूज हो जाएँगे।
उत्तर
150 दिनों के उपयोग के बाद फ्यूज होने की प्रायिकता p = 0.05
150 दिनों में उपयोग के बाद फ्यूज न होने की प्रायिकता q = 1 – 0.05 = 0.95
(i) P पाँचों में से कोई भी बल्ब 150 दिनों के उपयोग के बाद फ्यूज नहीं होगा
= (0.95)⁵
(ii) P (एक से अधिक बल्ब फ्यूज नहीं होंगे)
= (एक भी बल्ब फ्यूज न हो + एक बल्ब फ्यूज हो) की प्रायिकता
= P(0) + P (1) = (0.95)⁵ + ⁵C₁ x (0.95)⁴ x (0.05)
= (0.95)⁴[ 0.95 + 5 x 0.05]
= (0.95)⁴ [ 0.95 + 0.25]
= (0.95)⁴ x 1.2
(iii) P (एक से अधिक बल्ब फ्यूज होंगे) = (2 बल्ब + 3 बल्ब +4 बल्ब + 5 बल्ब) फ्यूज होने की अलग-अलग प्रायिकता
= P (2) + P (3) + P (4) + P (5)
= [P (0) + P (1) + P (2) + P (3) + P (4) + P (5) – [P (0) + P (1)]
= 1 – [P (0) + P (1)]
= 1- (0.95)⁴ x 1.2
(iv) P (कम-से-कम एक बल्ब फ्यूज होता है)
= P (1) + P (2) + P (3) + P (4) + P (5)
= P (0) + P (1) + P (2) + P (3) + P (4) + P (5)- P (0)
= 1 – P (0)
= 1- (0.95)⁵

प्रश्न 6:
एक थैले में 10 गेंदें हैं जिनमें से प्रत्येक पर 0 से 9 तक के अंकों में से एक अंक लिखा है। यदि थैले से 4 गेंदें उत्तरोत्तर पुनः वापस रखते हुए निकाली जाती है, तो इसकी क्या प्रायिकता है कि उनमें से किसी भी गेंद पर अंक 0 न लिखा हो ?
उत्तर

प्रश्न 7:
एक सत्य-असत्य प्रकार के 20 प्रश्नों वाली परीक्षा में माना कि एक विद्यार्थी एक न्याय्य (unbiased) सिक्के को उछाल कर प्रत्येक प्रश्न का उत्तर निर्धारित करता है। यदि पाँसे पर चित्त प्रकट हो, तो प्रश्न का उत्तर ‘सत्य’ देता है और यदि पट प्रकट हो, तो असत्य’ लिखता है। इसकी प्रायिकता ज्ञात कीजिए कि वह कम से कम 12 प्रश्नों का सही उत्तर देता है।
उत्तर
प्रश्न का सही उत्तर देने की प्रायिकता (p) = पाँसे पर चित्त आने की प्रायिकता = Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)

प्रश्न 8:
माना कि X का बंटन B (6, Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) )है। दर्शाएँ कि X = 3 अधिकतम प्रायिकता चाला परिणाम है।
उत्तर
यहाँ पर X का द्विपद बंटन है जहाँ

प्रश्न 9:
एक बहु-विकल्पीय परीक्षा में 5 प्रश्न हैं जिनमें प्रत्येक के तीन सम्भावित उत्तर हैं। इसकी क्या प्रायिकता है कि एक विद्यार्थी केवल अनुमान लगा कर चार या अधिक प्रश्नों के सही उत्तर दे देगा ?
उत्तर
माना X : सही उत्तरों की संख्या

प्रश्न 10:
एक व्यक्ति एक लॉटरी के 50 टिकट खरीदता है, जिसमें उसके प्रत्येक में जीतने की। प्रायिकता है। इसकी क्या प्रायिकता है कि वह (a) न्यूनतम एक बार (b) तथ्यत: एक बार (c) न्यूनतम दो बार, इनाम जीतेगा ?
उत्तर
माना X : जीतने की संख्या

प्रश्न 11:
एक पाँसे को 7 बार उछालने पर तथ्यतः दो बार 5 आने की प्रायिकता ज्ञात कीजिए।
उत्तर
मानी सफलता की प्रायिकता = p।

प्रश्न 12:
एक सँसे को 6 बार उछालने पर अधिकतम 2 बार छः आने की प्रायिकता ज्ञात कीजिए।
उत्तर
प्रश्नानुसार, n = 6, पाँसे की उछाल पर 6 आने की प्रायिकता अर्थात् सफलता की प्रायिकता

प्रश्न 13:
यह ज्ञात है कि किसी विशेष प्रकार की निर्मित वस्तुओं की संख्या में 10% खराब है। इसकी क्या प्रायिकता है कि इस प्रकार की 12 वस्तुओं के यादृच्छिक प्रतिदर्श में से 9 खराब है।
उत्तर
यहाँ n = 12, r = 9

प्रश्न 14.
100 बल्ब युक्त बॉक्स में, 10 दोषपूर्ण हैं। 5 बल्बों के नमूने से बाहर होने की संभावना, कोई भी दोषपूर्ण नहीं है
(a) Solutions Class 12 गणित-II Chapter-13 (प्रायिकता)
(b)
(c)
(d)
उत्तर
p =
q = n = 5, r = 0, P(X=0) =
Option (c) is correct

प्रश्न 15.
संभावना है कि एक छात्र तैराक नहीं है Solutions Class 12 गणित-II Chapter-13 (प्रायिकता) है। फिर संभावना है कि पांच छात्रों में से चार, तैराक हैं:

उत्तर
p = , q = , n = 5,r = 4