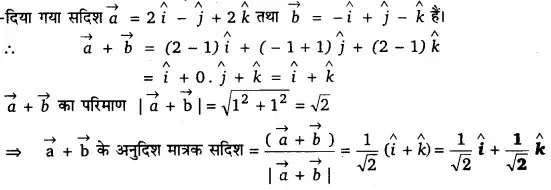NCERT Solutions Class 12 गणित-II Chapter-10 (सदिश बीजगणित)

NCERT Solutions Class 12 गणित-II 12 वीं कक्षा से Chapter-10 (सदिश बीजगणित) के उत्तर मिलेंगे। यह अध्याय आपको मूल बातें सीखने में मदद करेगा और आपको इस अध्याय से अपनी परीक्षा में कम से कम एक प्रश्न की उम्मीद करनी चाहिए।

हमने NCERT बोर्ड की टेक्सटबुक्स हिंदी गणित-II के सभी Questions के जवाब बड़ी ही आसान भाषा में दिए हैं जिनको समझना और याद करना Students के लिए बहुत आसान रहेगा जिस से आप अपनी परीक्षा में अच्छे नंबर से पास हो सके।

एनसीईआरटी प्रश्न-उत्तर

Class 12 गणित-II

पाठ-10 (सदिश बीजगणित)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

Exercise 10.1

प्रश्न 1.
उत्तर से 30° पूर्व में 40 किमी के विस्थापन को आलेखीय निरूपण कीजिए।
उत्तर
20 किमी को 1 सेमी मानते हुए 2 सेमी का एक रेखाखण्ड OP, OY की दायीं ओर OY के साथ 30° का कोण बनाते हुए खींचा गया। इस प्रकार सदिश $Solutions Class 12 गणित-II Chapter-10 (सदिश बीजगणित)$ OY से 30° पूर्व में किमी 40 किमी के विस्थापन को निरूपित करता है।

प्रश्न 2.
निम्नलिखित मापों को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।
(i) 10 किग्रा,
(ii) 2 मीटर उत्तर-पश्चिम,
(iii) 40°,
(iv) 40 वाट,
(v) 10^-19 कूलॉम,
(vi) 20 मी/से.
उत्तर
(i) अदिश-यहाँ इकाई किग्रा जो द्रव्यमान का मात्रक है तथा हम जानते हैं कि द्रव्यमान एक अदिश राशि है, अतः 10 किग्रा भी एक अदिश राशि है।
(ii) सदिश-2 मी उत्तर-पश्चिम एक सदिश राशि है क्योंकि इसमें परिमाण (2 मी) तथा दिशा । (उत्तर-पश्चिम) दोनों विद्यमान हैं।
(iii) अदिश-40° एक कोण को प्रदर्शित करता है हम जानते हैं कि कोण एक अदिश राशि है क्योंकि इसमें केवल परिमाण होता है।
(iv) अदिश-यहा इकाई वाट है जोकि शक्ति का मात्रक है तथा कार्य करने की शक्ति एक अदिश राशि है, अत: 40 वाट भी एक अदिश राशि है क्योंकि इसमें केवल परिमाण होता है।
(v) अदिश-10^-19 कुलाम एक अदिश राशि है क्योंकि इसमें केवल परिमाण विद्यमान है।
(vi) सदिश-यहाँ दिया गया मात्रक मी/से है जोकि त्वरण का मात्रक है तथा त्वरण एक सदिश राशि है। अत: 20 मी/से एक सदिश राशि है क्योंकि इसमें परिमाण के साथ दिशा भी विद्यमान है।

प्रश्न 3.
निम्नलिखित को अदिश एवं सदिश राशियों के रूप में श्रेणीबद्ध कीजिए
(i) समय कालांश
(ii) दूरी
(iii) बल
(iv) वेग
(v) कार्य
उत्तर
(i) अदिशे-समय कालांश एक अदिश राशि है क्योंकि इसमें केवल परिमाण होता है।
(ii) अदिश-दूरी एक अदिश राशि है क्योंकि इसमें केवल परिमाण होता है।
(iii) सदिश-बल एक सदिश राशि है क्योंकि इसमें परिमाण व दिशा दोनों विद्यमान है।
(iv) सदिश-वेग एक सदिश राशि है क्योंकि इसमें परिमाण व दिशा दोनों विद्यमान है।
(v) अदिश-कार्य एक अदिश राशि है क्योंकि इसमें केवल परिमाण होता है।

प्रश्न 4.
चित्र में निम्नलिखित सदिशों को पहचानिए
(i) सह आदिम
(ii) समान
(iii) संरेख परन्तु असमान

उत्तर
(i) सहआदिम $Solutions Class 12 गणित-II Chapter-10 (सदिश बीजगणित)$
(ii) $Solutions Class 12 गणित-II Chapter-10 (सदिश बीजगणित)$
(iii)

प्रश्न 5.

निम्नलिखित के उत्तर सत्य व असत्य के रूप में दीजिए–
(i) Solutions Class 12 गणित-II Chapter-10 (सदिश बीजगणित) संरेखीय हैं।
(ii) दो संरेख सदिशों का परिमाण सदैव समान होता है।
(iii) दो समान परिमाण वाले सदिश संरेख होते हैं।
(iv) दो समान परिमाण वाले संरेखीय सदिश समान होते हैं।
उत्तर
(i) क्योंकि प्रत्येक सदिश स्वयं के संरेख होता है। अत: कथन सत्य है।
(ii) दो संरेख सदिशों के परिमाण भिन्न-भिन्न हो सकते हैं। अत: कथन असत्य है।
(iii) असत्य
(iv) सत्य।

Exercise 10.2

प्रश्न 1.
निम्नलिखित सदिशों के परिमाण का परिकलन कीजिए

उत्तर

प्रश्न 2.
समान परिमाण वाले दो विभिन्न सदिश लिखिए।
उत्तर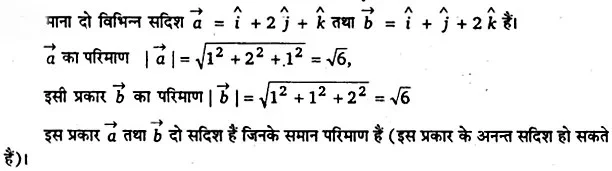

प्रश्न 3.
समान दिशा वाले दो विभिन्न सदिश लिखिए।
उत्तर

प्रश्न 4.
x और y के मान ज्ञात कीजिए ताकि सदिश

समान हों।
उत्तर

प्रश्न 5.
एक सदिश का प्रारम्भिक बिन्दु (2, 1) है और अन्तिम बिन्दु (-5, 7) है। इस सदिश के अदिश एवं सदिश घटक ज्ञात कीजिए।
उत्तर
माना सदिश के प्रारम्भिक वे अन्तिम बिन्दु क्रमशः A (2, 1), B (-5, 7) हैं।

प्रश्न 6.
सदिश

का योगफल ज्ञात कीजिए।
उत्तर

प्रश्न 7.
सदिश
के अनुदिश एक पात्रक सदिश ज्ञात कीजिए।
उत्तर

प्रश्न 8.
सदिश Solutions Class 12 गणित-II Chapter-10 (सदिश बीजगणित) के अनुदिश मात्रक सदिश ज्ञात कीजिए जहाँ विन्दु P और Q क्रमशः (1, 2, 3) और (4, 5, 6) हैं।
उत्तर
बिन्दु P(1, 2, 3) तथा Q(4, 5, 6) को मिलाने वाला सदिश

प्रश्न 9.

उत्तर

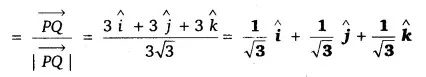
प्रश्न 10.
सदिश के अनुदिश एक ऐसा सदिश ज्ञात कीजिए। जिसका परिमाण 8 इकाई है।
उत्तर

प्रश्न 11.
दर्शाइए कि सदिश

संरेख हैं।
उत्तर

प्रश्न 12.
सदिश की दिक्-कोज्या ज्ञात कीजिए।
उत्तर

प्रश्न 13.
बिन्दुओं A(1,2,-3) एवं B(-1,-2,1) को मिलाने वाले एवं A से B की तरफ दिष्ट सदिश की दिक् – कोज्या ज्ञात कीजिए।
उत्तर
A (x1, y1, z1) और B (x2, y2, z2) को मिलाने वाले एवं A से B की तरफ ओर सदिश

प्रश्न 14.
दर्शाइए कि सदिश अक्षों OX, OY, OZ के साथ बराबर झुका हुआ है।
उत्तर
सदिश की दिक्-कोज्याएँ क्रमशः

चूँकि सदिश की दिक्-कोज्याएँ समान हैं अत: सदिश अक्षों से समान कोण बनाता है।

प्रश्न 15.
बिन्दुओं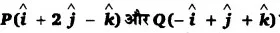

को मिलाने वाली रेखा को 2:1 के अनुपात में
(i) अन्तः,
(ii) बाह्य, विभाजित करने वाले विन्दु R का स्थिति सदिश ज्ञात कीजिए।
उत्तर
(i) अन्त: विभाजन

प्रश्न 16.
दो बिन्दुओं P (2, 3, 4) और Q(4, 1, -2) को मिलाने वाले सदिश का मध्यबिन्दुज्ञात कीजिए।
उत्तर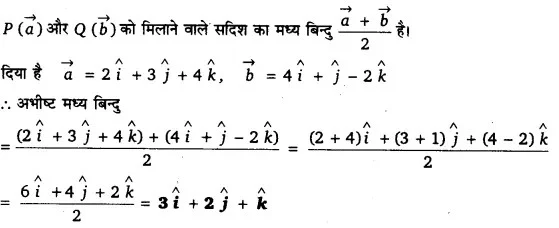

प्रश्न 17.
दर्शाइए कि बिन्दु A, B और C जिनके स्थिति सदिश क्रमशः

है, एक समकोण त्रिभुज के शीर्षों का निर्माण करते हैं।
उत्तर

प्रश्न 18.

उत्तर

प्रश्न 19.

उत्तर: (D)

Exercise 10.3

प्रश्न 1.

उत्तर:

प्रश्न 2.

उत्तर:

प्रश्न 3.
सदिश पर सदिश का प्रक्षेप ज्ञात कीजिए।
उत्तर:

प्रश्न 4.

उत्तर:

प्रश्न 5.

उत्तर:

प्रश्न 6.

उत्तर:

प्रश्न 7.
उत्तर:

प्रश्न 8.

उत्तर:

प्रश्न 9.

उत्तर:

प्रश्न 10.

उत्तर:

प्रश्न 11.

उत्तर:

प्रश्न 12.

उत्तर:

प्रश्न 13.

उत्तर:

प्रश्न 14.

उत्तर:

प्रश्न 15.

उत्तर:

प्रश्न 16.
दर्शाइए कि बिन्दु A(1,2,2, B(2,6, 3) और C(3, 10,- 1) संरेख हैं।
उत्तर:
दिया है, बिन्दु ABC के स्थिति सदिश क्रमशः (1, 2, 7), (2, 6, 3) और (3, 10,- 1) हैं।
माना O मूल बिन्दु है। तब ।