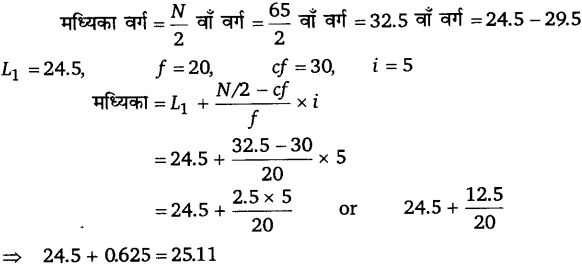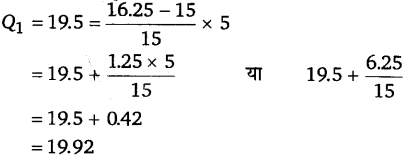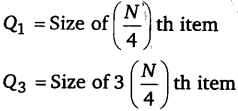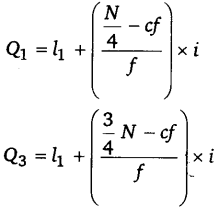NCERT Solutions Class 11 Economics in Hindi (अर्थशास्त्र) Chapter - 5 (केंद्रीय प्रवृत्ति की माप)

NCERT Solutions Class 11 अर्थशास्त्र में सांख्यिकी 11 वीं कक्षा से Chapter-5 (केंद्रीय प्रवृत्ति की माप) के उत्तर मिलेंगे। यह अध्याय आपको मूल बातें सीखने में मदद करेगा और आपको इस अध्याय से अपनी परीक्षा में कम से कम एक प्रश्न की उम्मीद करनी चाहिए। 

हमने NCERT बोर्ड की टेक्सटबुक्स हिंदी अर्थशास्त्र में सांख्यिकी के सभी Questions के जवाब बड़ी ही आसान भाषा में दिए हैं जिनको समझना और याद करना Students के लिए बहुत आसान रहेगा जिस से आप अपनी परीक्षा में अच्छे नंबर से पास हो सके।

एनसीईआरटी प्रश्न-उत्तर

Class 11 भारतीय अर्थव्यवस्था का विकास

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

पाठ-5 (केंद्रीय प्रवृत्ति की माप)

प्रश्न 1.

निम्नलिखित स्थितियों में कौन-सा औसत उपयुक्त होगा

(क) तैयार वस्त्रों के औसत आकार।

उत्तर :

बहुलक।

(ख) एक कक्षा में छात्रों की औसत बौद्धिक प्रतिभा।

उत्तर :

मध्यिका।

(ग) एक कारखाने में प्रति पाली औसत उत्पादन।

उत्तर :

बहुलक या समान्तर माध्य।

(घ) एक कारखाने में औसत मजदूरी।

उत्तर :

बहुलक या समान्तर माध्य।

(ङ) जब औसत से निरपेक्ष विचलनों का योग न्यूनतम हो।

उत्तर :

समान्तर माध्य।

(च) जब चरों की मात्रा अनुपात में हो।

उत्तर :

मध्यिका।

(छ) मुक्तांत बारम्बारता बंटन के मामले में।

उत्तर :

मध्यिका

प्रश्न 2.

प्रत्येक प्रश्न में दिए गए बहुविकल्पों में से सर्वाधिक उचित विकल्प को चिह्नित करें

(i) गुणात्मक मापन के लिए सर्वाधिक उपयुक्त औसत है

(क) समान्तर माध्य।

(ख) मध्यिका

(ग) बहुलक

(घ) ज्यामितीय माध्य

(ङ) इनमें से कोई नहीं

उत्तर :

(ख) मध्यिका।

(ii) चरंम मदों की उपस्थिति से कौन-सा औसत सर्वाधिक प्रभावित होता है

(क) मध्यिका

(ख) बहुलक

(ग) समान्तर माध्य

(घ) ज्यामितीय माध्य

(ङ) हरात्मक माध्ये

उत्तर :

(ग) समान्तर माध्य।

(iii) समान्तर माध्य से मूल्यों के किसी समुच्चय के विचलन का बीजगणितीय योग है

(क) दें

(ग) 1

(घ) इनमें से कोई नहीं

उत्तर :

(ग) 1

प्रश्न 3.

बताइए कि निम्नलिखित कथन सही हैं या गलत

(क) मध्यिका से मदों के विचलनों का योग शून्य होता है।

उत्तर :

गलत।

(ख) श्रृंखलाओं की तुलना के लिए मौत्र औसत ही पर्याप्त नहीं है।

उत्तर :

सही

(ग) समान्तर माध्ये एक स्थैतिक मूल्य है।

उत्तर :

गलत।

(घ) उच्च चतुर्थक शीर्ष 25 प्रतिशत मदों का निम्नतम मान है।

उत्तर :

सही।

(ङ) मध्यिका चरम प्रेक्षणों द्वारा अनुचित रूप से प्रभावित होती है।

उत्तर :

गलत।

प्रश्न 4.

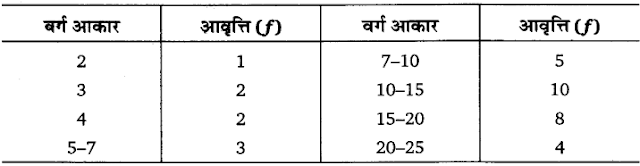
यदि नीचे दिए गए आँकड़ों का समान्तर माध्य 28 है तो

(क) लुप्त आवृत्ति का पता करें

(ख) श्रृंखला की मध्यिका ज्ञात करना

उत्तर :

(क) लुप्त आवृत्ति ज्ञात करना-

(ख) श्रृंखला की मध्यिका ज्ञात करना

लुप्त आवृत्ति A का मान 20 और मध्यिका का मान 27.41 है।

प्रश्न 5.

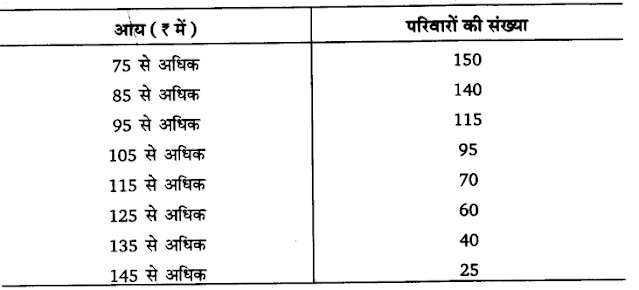
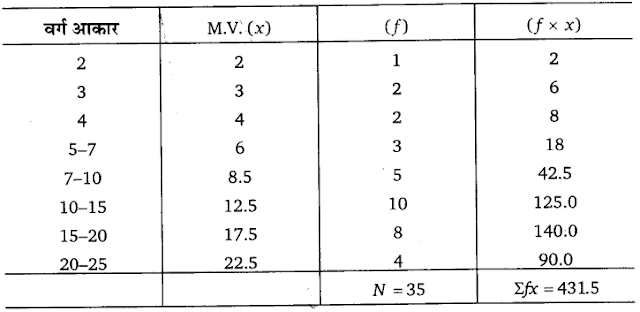
निम्नलिखित सूचना 150 परिवारों की दैनिक आय से सम्बद्ध है। समान्तर माध्य का परिकल कीजिए।

उत्तर :

प्रश्न 6.

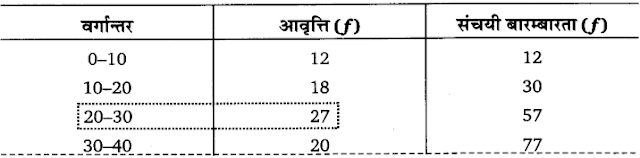
नीचे एक गाँव के 380 परिवारों की जोतों का आकार दिया गया है। जोत का मध्यिका आकार ज्ञात कीजिए।

उत्तर :

प्रश्न 7.

निम्नांकित श्रृंखला किसी कम्पनी में नियोजित मजदूरी की दैनिक आय से सम्बद्ध है। अभिकलन कीजिए

(क) निम्नतम 50 प्रतिशत मजदूरों की उच्चतम आय

(ख) शीर्ष 25 प्रतिशत मजदूरों द्वारा अर्जित न्यूनतम आय और

(ग) निम्नतम 25 प्रतिशत मजदूरों द्वारा अर्जित अधिकतम आय।

उत्तर :

(क) निम्नतम 50 प्रतिशत मजदूरों की उच्चतम आय ज्ञात करने के लिए हमें मध्यिका का मान ज्ञात करना चाहिए

निम्नतम 50 प्रतिशत मजदूरों की उच्चतम आय = ₹ 25.11॥

(ख) उच्चतम 25 प्रतिशत श्रमिकों की न्यूनतम आय ज्ञात करने के लिए चतुर्थक Qj को ज्ञात करना चाहिए।

उच्चतम 25 प्रतिशत श्रमिकों द्वारा अर्जित न्यूनतम आय = ₹ 19.92

(ग) निम्नतम 25 प्रतिशत श्रमिकों की उच्चतम आय ज्ञात करने के लिए उच्च चतुर्थक Q3 ज्ञात करना चाहिए

निम्नतम 25 प्रतिशत मजदूरों द्वारा अर्जित अधिकतम आय = ₹ 29.19

प्रश्न 8.

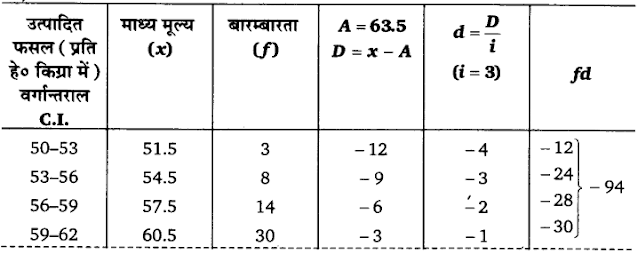
निम्नांकित सारणी में किसी गाँव में 150 खेतों में गेहूं की प्रति हेक्टेयर पैदावार दी गई है। उत्पादित फसलों का समान्तर माध्य, मध्यिका तथा बहुलक परिकलित कीजिए

उत्पादित फसले

(प्रति हेक्टे० किग्रा में) :     50-53   53-56   56-59   59-62   62-65   65-68   68-71   71-74   74-77

खेतों की संख्या :                  3            8           14         30        36          28          16         10          5

उत्तर :

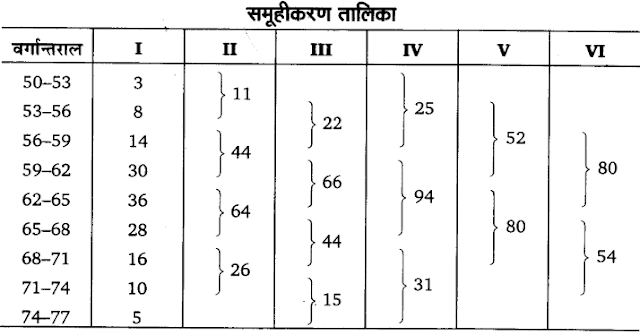
बहुलक ज्ञात करने के लिए निम्नांकित सँरणी बनाएँगे

परीक्षोपयोगी प्रश्नोत्तर

बहुविकल्पीय प्रश्न

प्रश्न 1. समान्तर माध्य का दोष है

(क) इसे निकालते समय समूह के सभी पदों का प्रयोग होता है।

(ख) समूह के सभी पदों को उनके आकार के अनुपात में बाँट दिया जाता है।

(ग) यह निश्चित और सदा एक ही होता है।

(घ) इसकी गणना में असाधारण एवं सीमान्त मूल्य का अधिक प्रभाव रहता है।

उत्तर :

(घ) इसकी गणना में असाधारण एवं सीमान्त मूल्य का अधिक प्रभाव रहता है।

प्रश्न 2.

“समान्तर माध्य किसी वितरण का केन्द्रीय मूल्य है।” यह कथन है

(क) किंग का

(ख) मिल का

(ग) मेहता का

(घ) पीगू का

उत्तर :

(ख) मिल की।

प्रश्न 3.

समंकमाला के पदों के जोड़ में उनकी संख्या 6, 2, 5, 3 का भाग देने से जो मूल्य प्राप्त होता है वह ………………………………….. कहलाता है।

(क) बहुलक

(ख) मध्यिका

(ग) समान्तर माध्य

(घ) कल्पित माध्य

उत्तर :

(ग) समान्तर माध्य।

प्रश्न 4.

बहुलक का गुण नहीं है

(क) कभी-कभी एक समूह में दो-या-दो से अधिक बहुलक भी हो सकते हैं।

(ख) गुणात्मक तथ्यों का भी बहुलक ज्ञात किया जा सकता है।

(ग) यह अति सीमान्त पदों से प्रभावित नहीं होता।

(घ) प्रर्तिदर्श के परिवर्तन के साथ बहुलक में परिवर्तन नहीं होता।

उत्तर :

(क) कभी-कभी एक समूह में दो-या-दो से अधिक बहुलक भी हो सकते हैं।

प्रश्न 5.

“औसत वह संख्या है जो समस्त वर्ग का प्रतिनिधित्व करती है।’ कथन है

(क) प्रो० कॉनर का

(ख) प्रो० यूल का

(ग) बोडिंगटन का

(घ) क्लार्क का

उत्तर :

(घ) क्लार्क को

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.

केन्द्रीय प्रवृत्ति की माप किसे कहते हैं?

उत्तर :

केन्द्रीय प्रवृत्ति की माप एक ऐसा प्रतिरूपी मूल्य है जिसका प्रयोग श्रेणी के सभी मूल्यों का प्रतिनिधित्व करने के लिए किया जाता है।

प्रश्न 2.

समांन्तर माध्य किसे कहते हैं?

उत्तर :

समान्तर माध्ये वह मूल्य है जो किसी श्रेणी के समस्त पदों के मूल्य के योग में उनकी संख्या का भाग देने से प्राप्त होता है।

प्रश्न 3.

समान्तर माध्य के दो गुण बताइए।

उत्तर :

• इसमें बीजगणित का प्रयोग सम्भव है। दो-या-दो से अधिक श्रेणियों का सामूहिक औसत इनके अलग-अलग औसतों की सहायता से निकाला जा सकता है।
• समूह के सभी पदों को उनके आकार के अनुपात में बाँट दिया जाता है।

प्रश्न 4.

समान्तर माध्य के दो दोष बताइए।

उत्तर :

• समंकमाला की आकृति देखकर इसका अनुमान नहीं लगाया जा सकता।
• समंकमाला का कोई भी मूल्य ज्ञात न होने पर इसकी गणना नहीं की जा सकती।

प्रश्न 5.

पद विचलन रीति में समान्तर माध्य निकालने का सूत्र लिखिए।

उत्तर :

X = A + 

प्रश्न 6.

श्रेणी के प्रत्येक मूल्य को समान भार देने की दिशा में सरल व भारित समान्तर माध्या कैसे होते हैं?

उत्तर :

बराबर।

प्रश्न 7.

मध्यिका के दो गुण बताइए।

उत्तर :

• इसका निर्धारण निश्चित और शुद्ध होता है।
• गुणात्मक विशेषताओं का अध्ययन करने में यह अन्य माध्यों से श्रेष्ठ है।

प्रश्न 8.

मध्यिका की दो सीमाएँ बताइए।

उत्तर :

• मध्यिका के पदों की संख्या से गुणा करने पर पदों का कुल योग मालूम नहीं होता।
• इसे ज्ञात करने के लिए समस्त पदों को आरोही या अवरोही क्रम में व्यवस्थित करना पड़ता है।

प्रश्न 9.

अविच्छिन्न श्रेणी में मध्यिका का सूत्र दीजिए।

उत्तर :

सर्वप्रथम

(i) m = Size of \frac { N }{ 2 }th item की सहायता से निकाला जाएगा। तत्पश्चात् यह सूत्र लगाया जाएगा   M  l₁ (m -c)।

प्रश्न 10.

भूयिष्ठक का अर्थ एवं परिभाषा दीजिए।

उत्तर :

किसी भी समंकमाला में जो पद सबसे अधिक बार आता है अथवा जिसकी आवृत्ति सबसे अधिक होती है, वही बहुलक कहलाता है। काउडेन के शब्दों में “एक वितरण का बहुलक वह मूल्य है, जिसके निकट श्रेणी की इकाइयाँ अधिक-से-अधिक केन्द्रित होती हैं। उसे मूल्यों की श्रेणी का सबसे अधिक प्रतिरूपी माना जाता है।”

प्रश्न 11.

बहुलक के दो गुण बताइए।

उत्तर :

• यह अति सीमान्त पदों से प्रभावित नहीं होता।
• कभी-कभी एक समूह में दो-या-दो से अधिक बहुलके भी हो सकते हैं।

प्रश्न 12.

बहुलक के दो दोष बताइए।

उत्तर :

• सभी पदों पर आधारित न होने के कारण इसका बीजीय विवेचन सम्भव नहीं है।
• कभी-कभी एक समूह में दो-या-दो से अधिक बहुलक भी हो सकते हैं।

प्रश्न 13.

बहुलक के दो उपयोग बताइए। अथवा बहुलक का क्या व्यावहारिक प्रयोग है?

उत्तर :

• उद्योग व प्रशासन के क्षेत्र में इसकी सहायता से औसत उत्पादन ज्ञात किया जाता है तथा विभिन्न विभागों की कार्यक्षमता की तुलना की जाती है।
• मौसम सम्बन्धी पूर्वानुमानों में भी इसी का प्रयोग होता है।

प्रश्न 14.

अविच्छिन्न श्रेणी में बहुलक का सूत्र दीजिए।

उत्तर :

लघु उत्तरीय प्रश्न

प्रश्न 1.

केन्द्रीय प्रवृत्ति क्या है? परिभाषा लिखिए।

उत्तर :

केन्द्रीय प्रवृत्ति से आशय किसी सांख्यिकी श्रृंखला के केन्द्रीय मूल्य या प्रतिनिधि मूल्य से है। किसी भी मनुष्य के लिए आँकड़ों के एक बहुत बड़े समूह को समझना या अपनी स्मृति में रखना कठिन होता है। इसलिए वह ऐसे मूल्य का ज्ञान प्राप्त करना पसन्द करेगा जो किसी श्रेणी के सभी आँकड़ों की विशेषताओं का प्रतिनिधित्व करता हो। इस प्रकार के मूल्य को केन्द्रीय प्रवृत्ति के माप’ अथवा औसत या माध्य कहा जाता है। उदाहरण के लिए भारत के करोड़ों लोगों के आय सम्बन्धी आँकड़ों को समझना तथा याद रखना कठिन कार्य होगा परन्तु यदि यह कहा जाए कि वर्ष 2012 में भारत के लोगों की औसत आय १ 23,000 प्रतिवर्ष है तो हम सरलता से भारत के अधिकतर लोगों की आर्थिक स्थिति का अनुमान लगा सकेंगे। इस औसत मूल्य को ही श्रृंखला का केन्द्रीय माप कहा जाता है। इसे स्थिति सम्बन्धी माप भी कहते हैं। अत: केन्द्रीय प्रवृत्ति के माप से आशय सांख्यिकीय विश्लेषण की उन विधियों से है जिनके द्वारा किसी श्रेणी के चर को ऐसा मूल्य अर्थात् औसत ज्ञात किया जाता है जो समस्त श्रेणी का प्रतिनिधित्व करता है।

1. क्रोक्सटन तथा काउडेन के अनुसार – “आँकड़ों के विस्तार के अन्तर्गत स्थित एक ऐसे मूल्य को जिसका प्रयोग श्रृंखला के सभी मूल्यों का प्रतिनिधित्व करने के लिए किया जाता है, औसत कहा जाता है। चूंकि औसत श्रृंखला के विस्तार के अन्तर्गत स्थित होता है इसलिए इसे केन्द्रीय प्रवृत्ति की माप भी कहा जाता है।

2. क्लार्क के अनुसार – “औसत वह संख्या है जो समस्त वर्ग का प्रतिनिधित्व करती है।”

प्रश्न 2.

मध्यिका का अर्थ व गुण बताइए।

उत्तर :

मध्यिका का अर्थ-मध्यिका आरोही अथवा अवरोही क्रम में अनुविन्यसित समंकमाला के विभिन्न पदों के मध्य का मूल्य होती है और वह समंकमाला को दो भागों में इस प्रकार बाँटती है कि उसके एक ओर के सभी पद उससे कम मूल्य के तथा दूसरी ओर के सब पद उससे अधिक मूल्य के होते हैं।

मध्यिका के गुण – मध्यिका के प्रमुख गुण निम्नलिखित हैं

• यह बहुत सरल है और इसको बड़ी सुगमता से समझा जा सकता है।
• इसका निर्धारण निश्चित और शुद्ध होता है।
• इसे पदों की कुल संख्या मात्र से ज्ञात किया जा सकता है।
• मध्यिका को बिन्दु रेखाओं द्वारा प्रदर्शित किया जा सकता है।
• मध्यिका पर चर मूल्यों का कोई प्रभाव नहीं पड़ता।
• मध्य विचलन की गणना में मध्यिका का और अधिक बीजीय विवेचन सम्भव है।
• गुणात्मक विशेषताओं को अध्ययन करने में यह अन्य माध्यों से श्रेष्ठ है।
• मध्यिका से पदों के विचलनों का योग अन्य किसी भी विधि से निकाले गए विचलनों के योग से कम होता है।

प्रश्न 3.

मध्यिका के प्रमुख दोष बताइए। मध्यिका के क्या उपयोग हैं?

उत्तर :

मध्यिका के प्रमुख दोष निम्नलिखित हैं

• मध्यिका के पदों की संख्या से गुणा करने पर पदों का कुल योग मालूम नहीं होता।
• यदि पदों के विस्तार में असाधारण भिन्नता हो तो यह भ्रामक निष्कर्ष देती है।
• इसे ज्ञात करने के लिए समस्त पदों को आरोही (ascending) या अवरोही (descending) क्रम में व्यवस्थित करना पड़ता है।
• इसको ज्ञात करने के लिए समस्त समंकों का प्रयोग नहीं होता।
• यदि मध्यपद दो वर्गों के बीच आता है तो मध्यिका को ठीक-ठीक ज्ञात करना कठिन हो जाता है।
• सरल गणितीय सूत्र से इसका अनुमान नहीं लगाया जा सकता।
• यदि पदों की संख्या सम (even) है तो मध्यिका वास्तविक मूल्य नहीं होता।
• यदि पदों की संख्या कम हो या मध्य पद के ऊपर अथवा नीचे पदों का फैलाव अनियमित हो तो मध्यिका एक प्रतिनिधि माप नहीं रहता।

मध्यिका के उपयोग – मध्यिका समझने में सरल है; अत: व्यावहारिक उद्देश्यों के लिए इसका बहुत अधिक उपयोग होता है। इसके द्वारा गुणात्मक तथ्यों जैसे—बुद्धिमत्ता, स्वास्थ्य आदि; का भी अध्ययन : किया जा सकता है। इसी कारण सामाजिक समस्याओं के विश्लेषण में यह अत्यधिक उपयोगी है। यही उन दशाओं में अधिक उपयोगी है, जहाँ अति सीमान्त पदों को महत्त्व नहीं दिया जाता अथवा वितरण विषम होता है।

प्रश्न 4.

बहुलक क्या है? बहुलक के गुण बताइए।

उत्तर :

बहुलक का अर्थबहुलक वह मूल्य है जो समंकमाला में सबसे अधिक बार आता है अथवा जिसकी आवृत्ति सबसे अधिक होती है। बहुलक के गुण-बहुलक के प्रमुख गुण निम्नलिखित हैं

• यह एक सरल एवं लोकप्रिय माध्य है। कुछ दशाओं में तो यह केवल निरीक्षण द्वारा ही ज्ञात किया जा सकता है।
• इसका मूल्य रेखाचित्र द्वारा भी निर्धारित किया जा सकता है।
• यह वितरण में सर्वाधिक सम्भावित मूल्य होता है।
• गुणात्मक तथ्यों का भी बहुलक ज्ञात किया जा सकता है।
• यह अति सीमान्त पदों से प्रभावित नहीं होता।
• यह श्रेणी के एक महत्त्वपूर्ण भाग का वास्तविक मूल्य होता है।
• यह समूह की सर्वोत्तम प्रतिनिधि होता है।
• प्रतिदर्श के परिवर्तन के साथ बहुलक में परिवर्तन नहीं होता।

प्रश्न 5.

बहुलक के दोष बताइए। इसके क्या उपयोग हैं?

उत्तर :

बहुलक के दोष-बहुलक के प्रमुख दोष निम्नलिखित हैं–

• यदि श्रेणी के सभी पदों की आवृत्तियाँ समान हैं तो बहुलक का निर्धारण नहीं किया जा सकता।
• कभी-कभी एक समूह में दो-या-दो से अधिक बहुलक भी हो सकते हैं।
• यदि श्रेणी का वितरण अनियमित है तो इसे शुद्ध रूप में नहीं निकाला जा सकता।
• यह चरम सीमाओं की उपेक्षा करता है जो कि गणितीय दृष्टि से उचित नहीं है।
• सभी पदों पर आधारित न होने के कारण इसका बीजीय विवेचन सम्भव नहीं है।
• यह श्रेणी का पूर्ण रूप से प्रतिनिधित्व नहीं करता।।
• वर्ग विस्तार में परिवर्तन कर देने पर बहुलक भी बदल जाएगा।

बहुलक के उपयोग – उपर्युक्त दोषों के बावजूद दैनिक जीवन तथा व्यापारिक क्षेत्र में बहुलक का बहुत अधिक उपयोग किया जाता है। यह शीघ्रता व सरलता से समझ में आ जाता है, इसलिए व्यावसायिक जीवन में इसका प्रयोग दिन-प्रतिदिन बढ़ता जा रहा है। व्यापारिक पूर्वानुमानों में यह एक महत्त्वपूर्ण पथ-प्रदर्शक है। उद्योग व प्रशासन के क्षेत्र में इसकी सहायता से औसत उत्पादन ज्ञात किया जाता है तथा विभिन्न विभागों की कार्यक्षमता की तुलना की जाती है। किसी वस्तु के उत्पादन में उसकी लागत का अनुमान बहुलक समय के निर्धारण द्वारा आसानी से लगाया जा सकता है। विभिन्न वस्तुओं की लोकप्रिंयता का अध्ययन बहुलक द्वारा ही किया जाता है। मौसम सम्बन्धी पूर्वानुमानों में भी इसी का प्रयोग होता है।

प्रश्न 6.

एक आदर्श माध्य के गुण बताइए।

उत्तर :

एक आदर्श माध्य के गुण

• माध्य स्पष्ट तथा स्थिर होना चाहिए। दूसरे शब्दों में, माध्य श्रेणी के न्यूनतम तथा अधिकतम मूल्यों से कम-से-कम प्रभावित होना चाहिए।
• माध्य समग्र का प्रतिनिधि होना चाहिए।
• माध्य निकालने तथा समझने में सरल होना चाहिए।
• वह समंकमाला के समस्त पदों पर आधारित होना चाहिए।
• वह सीमान्त पदों को समुचित महत्त्व देता हो।
• उस पर संख्याओं के परिवर्तन का कम-से-कम प्रभाव पड़ना चाहिए।
• वह एक निरपेक्ष संख्या होनी चाहिए। दूसरे शब्दों में, वह प्रतिशत में या अन्य कोई सापेक्ष रीति में व्यक्त नहीं होनी चाहिए।
• वह एक निश्चित संख्या होनी चाहिए।
• उसका प्रयोग अंकगणितीय व बीजगणितीय विधियों द्वारा किया जा सके।

प्रश्न 7.

सरल व भारित समान्तर माध्य की तुलना कीजिए।

उत्तर :

सरल व भारित समान्तर माध्य की तुलना

1. श्रेणी के प्रत्येक मूल्य को समान भार देने की दशा में सरल व भारित समान्तर माध्य बराबर होते हैं।

                                                            = w

2. जब श्रेणी के छोटे मूल्यों को अधिक भार और बड़े मूल्यों को कम भार दिया जाता है, तब सरल समान्तर माध्य भारित समान्तर माध्य से अधिक होता है।

                                                            = w

3. जब श्रेणी के छोटे मूल्यों को कम भार तथा बड़े मूल्यों को अधिक भार दिया जाता है, तब सरल समान्तर माध्य भारित समान्तर माध्य से कम होता है।

                                                               = w

प्रश्न 8.

समान्तर माध्य, मध्यिका एवं बहुलक में परस्पर सम्बन्ध दर्शाइए।

उत्तर :

समान्तर माध्य () मध्यिका (M) तथा बहुलक (Z) में सम्बन्ध आवृत्ति वितरण की प्रकृति पर निर्भर करता है। आवृत्ति वितरण दो प्रकार का होता है

1. सममित आवृत्ति वितरण – इस स्थिति में X, M तथा Z के मूल्य एक-दूसरे के समान होते हैं

= M = Z

2. असममितीर्य आवृत्ति वितरण – इस स्थिति में (X – Z) सामान्यत: 3(X – M) के बराबर होते हैं अर्थात्

(– Z) = 3(– M)

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.

समान्तर माध्य किसे कहते हैं? समान्तर माध्य के गुण-दोषों की व्याख्या कीजिए।

उत्तर :

समान्तर माध्य का अर्थ

समान्तर माध्य (Arithmetic Mean) केन्द्रीय प्रवृत्ति का सबसे सरल एवं लोकप्रिय माप है। सामान्यतः औसत शब्द का प्रयोग इसी माध्य के लिए किया जाता है। यह सभी माध्यों में उत्तम माना जाता है। इसको इस प्रकार परिभाषित किया जा सकता है-“किसी भी श्रेणी के समस्त पदों के मूल्य के योग में उनकी संख्या का भाग देने से समान्तर मध्य प्राप्त होता है।”

साधारण शब्दों में, समंकमाला के पदों के जोड़ में उनकी संख्या का भाग देने से जो राशि प्राप्त होती है, उसे माध्य के रूप में परिभाषित किया जा सकता है।

किंग के अनुसार-“किसी श्रेणी के पदों के मूल्यों के योग में उनकी संख्या का भाग देने से जो मूल्य प्राप्त होता है, उसे समान्तर माध्य के रूप में परिभाषित किया जा सकता है।” मिल के अनुसार-“समान्तर माध्य किसी वितरण का केन्द्रीय मूल्य है।”

समान्तर माध्य के गुण

• इसका अर्थ एक सामान्य व्यक्ति के लिए भी समझना आसान है।
• उपलब्ध आँकड़ों की सहायता से इसकी गणना बहुत सरल है। ।
• इसमें बीजगणित का प्रयोग सम्भव है। दो-या-दो से अधिक श्रेणियों का सामूहिक औसत इनके अलग-अलग औसतों की सहायता से निकाला जा सकता है।
• इसे निकालते समय समूह के सभी पदों का प्रयोग होता है।
• समूह के सभी पदों को उनके आकार के अनुपात में बाँट दिया जाता हैं।
• यह निश्चित और संदा एक ही होता है।
• तुलनात्मक अध्ययन के लिए यह अधिक लोकप्रिय है।

समान्तर माध्य के दोष

• समंकमाला में समान्तर माध्य हो, यह आवश्यक नहीं है।
• समंकमाला की आकृति देखकर इसका अनुमान नहीं लगाया जा सकता।
• इसकी गणना में असाधारण एवं सीमान्त मूल्य का अधिक प्रभाव रहता है।
• समंकमाला का कोई भी मूल्य ज्ञात न होने पर इसकी गणना नहीं की जा सकती।
• गुणात्मक सामग्री के लिए इसका प्रयोग नहीं किया जा सकता।
• इसे लेखाचित्र द्वारा प्रदर्शित नहीं किया जा सकता।
• अनुपात वे दर आदि के अध्ययन के लिए यह अनुपयुक्त है।
• उपर्युक्त दोषों के होते हुए भी इसका प्रयोग सामाजिक तथा आर्थिक समस्याओं के अध्ययन में किया जाता है।

प्रश्न 2.

सरल समान्तर माध्य की गणना प्रक्रिया को उदाहरण सहित समझाइए।

उत्तर :

सरल समान्तर माध्य की गणन क्रिया सरल समान्तर माध्य की गणना तीन प्रकार से करते हैं

(I) व्यक्तिगत श्रेणी,

(II) खण्डित श्रेणी एवं

(III) अविच्छिन्न श्रेणी।

(1) व्यक्तिगत श्रेणी

व्यक्तिगत श्रेणी द्वारा समान्तर माध्य निकालने की दो रीतियाँ हैं

(अ) प्रत्यक्ष रीति तथा

(ब) लघु रीति।

(अ) प्रत्यक्ष रीति – इस रीति में श्रेणी के सभी पदों का योग करने के बाद उनको पदों की संख्या से भाग दिया जाता है।

   सूत्र रूप में, = 
   यहाँ, = समान्तर माध्य
   ∑X = पद मूल्यों का योग
   N = पदों की संख्या

गणन क्रिया –

• पद मूल्यों का योग (∑X) ज्ञात करते हैं।
• पद संख्या (N) ज्ञात करते हैं।
• पद मूल्यों के योग में पद संख्या (N) का भाग देते हैं। परिणाम समान्तर माध्य होता है।

(ब) लघु रीति – इस रीति में गणन क्रिया निम्नलिखित प्रकार से की जाती है

• किसी संख्या को कल्पित माध्य (A) मान लेते हैं।
• कल्पित माध्य (A) की पद मूल्यों (X) से तुलना करके विचलन मालूम करते हैं d = X – A
• विचलनों (d) का योग (d) ज्ञात करते हैं।
• पदों की संख्या (N) ज्ञात करते हैं। फिर निम्नलिखित सूत्र का प्रयोग करते हैं   = A + 

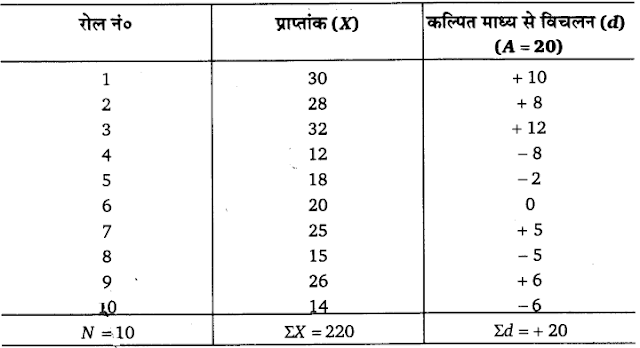
उदाहरण 1. 15 पदों का आकार निम्नलिखित है। प्रत्यक्ष व लघु रीति द्वारा समान्तर माध्य का परिकलन कीजिए।

रोल नं० :   1    2    3    4    5   6    7   8    9    10

प्राप्तांक :  30 28 32  12  18 20 25 15  26   14

उत्तर :

(II) खण्डित श्रेणी

खण्डित श्रेणी द्वारा समान्तर माध्य निकालने की दो रीतियाँ हैं

(अ) प्रत्यक्ष रीति तथा

(ब) लघु रीति।

(अ) प्रत्यक्ष रीति – इस रीति में गणन क्रिया निम्नलिखित प्रकार से की जाती है–

• पद मूल्यों (X) और आवृत्ति (ƒ) का गुणा करते हैं (X × ƒ)
• गुणनफलों (ƒ × X) का योग ज्ञात करते हैं (∑fX)
• आवृत्तियों का योग (∑ƒ) या (N) ज्ञात करते हैं।
• निम्नांकित सूत्र का प्रयोग करते हैं
• \overline { X } \frac { SfX }{ NSf }

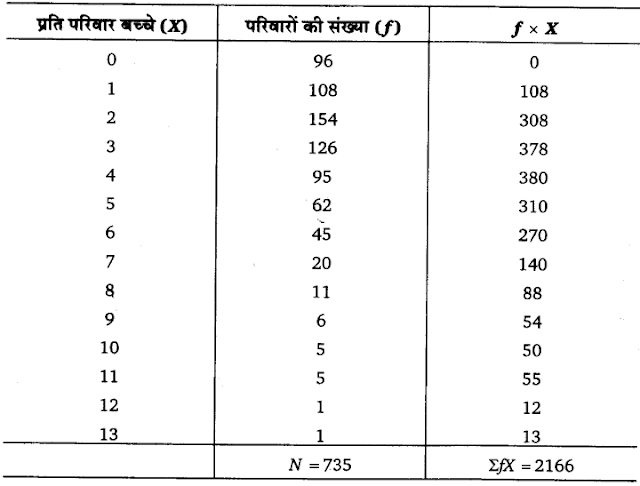
उदाहरण 2. प्रति परिवार जन्म लेने वाले औसत बच्चों की संख्या ज्ञात कीजिए-

उत्तर :

(ब) लघु रीति – इस रीति में गणन क्रिया निम्नलिखित प्रकार से की जाती है

• मूल्यों में से किसी एक को कल्पित माध्य (A) मान लेते हैं।
• कल्पित माध्य (A) से श्रेणी प्रत्यक्ष मूल्य का विचलन (dx) निकालते हैं d = (x – A)
• विचलनों को उनकी आवृत्तियों से गुणा करते हैं–(d × f)
• इन गुणनफलों का योग निकालते हैं। अन्त में निम्नलिखित सूत्र का प्रयोग करते हैं
• = A + 

उदाहरण 3. निम्नलिखित समंकों में से प्रत्यक्ष व लघु रीति द्वारा समान्तर माध्य परिकलित कीजिए

उत्तर :

(III) अविच्छिन्न श्रेणी

इसमें सर्वप्रथम श्रेणी में वर्गों के मध्यमान (X) ज्ञात किए जाते हैं। समान्तर मध्य ज्ञात करने की मुख्य रीतियाँ निम्नलिखित हैं–

(अ) प्रत्यक्ष रीति – सर्वप्रथम वर्गों के मध्य मूल्य (M.V.) निकाले जाते हैं। इसके बाद वही क्रिया अपनाई जाती है, जो खण्डित श्रेणी में प्रयुक्त की जाती है।

(ब) लघु रीति – इसके अन्तर्गत सर्वप्रथम वर्गों के मध्य मूल्य ज्ञात किए जाते हैं। फिर वही क्रिया अपनाई जाती है, जो खण्डित श्रेणी में प्रयुक्त की जाती है।

उदाहरण 4. निम्नलिखित समंकों से समान्तर मध्य ज्ञात कीजिए

उत्तर :

उदाहरण 5. निम्नांकित सारणी में प्रत्यक्ष व लघु रीति द्वारा समान्तर माध्य ज्ञात कीजिए

उत्तर :

(स) पद विचलन रीति – गणन क्रिया निम्नलिखित प्रकार से की जाती है

(i) सर्वप्रथम सभी वर्गान्तरों के मध्य बिन्दु ज्ञात करते हैं।

(ii) मध्य बिन्दुओं में से किसी एक को कल्पित माध्य (A) मान लेते हैं।

(iii) कल्पित माध्य (A) में से प्रत्येक मध्य मूल्य के विचलन ज्ञात करते हैं।

(iv) विचलनों में वर्ग विस्तार से भाग देकर पद विचलन ज्ञात करते हैं। (d)

(v) पद विचलन की आवृत्तियों से गुणा करके गुणनफलों का योग कर लेते हैं (Σƒd’) और इस योग में N से भाग देते हैं।

(vi) निम्नलिखित सूत्र का प्रयोग करते हैं

= A +  × i

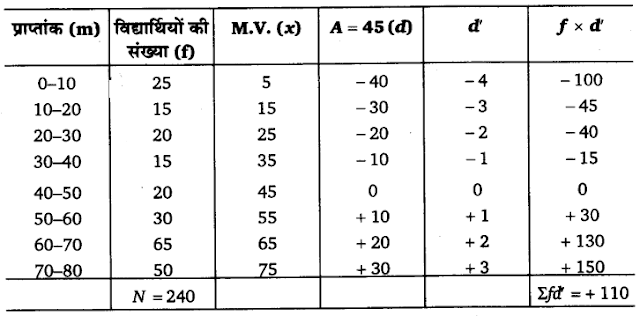
उदाहरण 6. निम्नांकित सारणी में पद विचलन रीति द्वारा समान्तर माध्य ज्ञात कीजिए–

उत्तर :

प्रश्न 3.

भारित समान्तर माध्य से क्या आशय है? इसकी गणना विधि समझाइए। उपयुक्त उदाहरण भी दीजिए।

उत्तर :

भारितसमान्तर माध्य

जब माध्य निकालते समय कुछ पदों को अन्य पदों की अपेक्षा अधिक महत्त्व दिया जाता है तो उसे ‘भार’ कहते हैं और वह माध्य भारित माध्य कहलाता है।

बोडिंगटन के शब्दों में – “भारित माध्य वह है, जिसे निकालने के लिए प्रत्येक पद को भार से गुणा किया जाता है और इस प्रकार प्राप्त की गई संख्याओं को जोड़कर भार के योग से भाग दे दिया जाता है।”

भारित समान्तर माध्य की गणना करना – भारित समान्तर माध्य की गणन क्रिया निम्नलिखित प्रकार से की जाती है

प्रत्यक्ष रीति-

• श्रेणी के प्रत्येक पद को उसके महत्त्व के अनुसार भार प्रदान किया जाता है।
• श्रेणी के मूल्यों तथा उनके तत्सम्बन्धी भारों की गुणा की जाती है तथा इनका योग निकाल लिया जाता है।
• इस योग को भारों के योग से विभाजित कर दिया जाता है।
• अन्त में निम्नलिखित सूत्र का प्रयोग किया जाता है
• \overline { X } w=\frac { \Sigma XW }{ \Sigma W }

यहाँ, w = भारित समान्तर माध्य
ΣXW = मूल्य व भारों के गुणनफलों का योग
ΣW = भारों का योग

लघु रीति –

• श्रेणी के प्रत्येक पद को उसके महत्त्व के अनुसार भार प्रदान किया जाता है।
• काल्पनिक भारित माध्य मानकरे मूल्यों से विचलन लिए जाते हैं।
• विचलनों तथा तत्सम्बन्धी भारों के गुणनफल का योग ज्ञात किया जाता है।
• अन्त में इस योग को भारों के योग से भाग दे दिया जाता है। जो मूल्य आता है, उसे काल्पनिक भारित माध्य (A) में जोड़ दिया जाता है।
• अन्त में निम्नलिखित सूत्र का प्रयोग किया जाता है|
• w = A + 

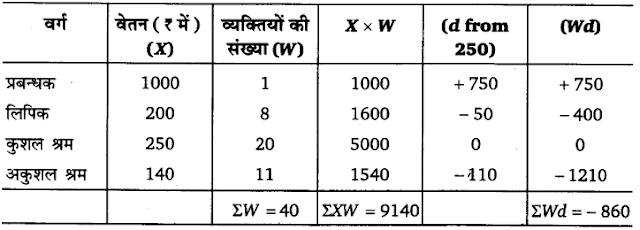
उदाहरण 7. एक कारखाने के कर्मचारियों का मासिक वेतन और उनकी संख्या निम्नांकित सारणी में वर्णित हैं मासिक वेतन का प्रत्यक्ष व लघु रीति द्वारा भारत मध्य ज्ञात कीजिए

उत्तर :

प्रश्न 4.

मध्यिका को परिभाषित कीजिए तथा उसके गुण, दोष व उपयोग बताइए। अथवा मध्यिका के गुण-दोषों पर टिप्पणी कीजिए।

उत्तर :

मध्यिका

अर्थ एवं परिभाषा – मध्यिका आरोही अथवा अवरोही क्रम में अनुविन्यसित समंकमाला के विभिन्न पदों के मध्य का मूल्य (middle item) होती है और वह समंकमाला को दो भागों में इस प्रकार बाँटती है। कि उसके एक ओर के सब पद उससे कम मूल्य के तथा दूसरी ओर के सब पद उससे अधिक मूल्य के होते हैं।

प्रो० कॉनर के शब्दों में – “मध्यिका समंक श्रेणी का वह पद है, जो समूह को दो समान भागों में इस प्रकार विभक्त करता है कि एक भाग में समस्त मूल्य मध्यिका से अधिक और दूसरे भाग में अन्य मूल्य मध्यिका से कम हों।”

प्रो० युल एवं केण्ड्राल के शब्दों में – “मध्यिका केन्द्रीय या मध्य मूल्य होता है, जबकि समूह के मूल्यों अर्थात् आवृत्तियों को इनके परिमाण के अनुसार क्रम से लिखा जाए या इस प्रकार लिखा जाए कि बड़े तथा छोटे मूल्य समाप्त आवृत्तियों में बँट जाएँ।”

डॉ० बाउले के शब्दों में – “यदि एक समूह के पदों को उनके मूल्यों के अनुसार क्रमबद्ध किया जाए, तब लगभग मध्य पद का मूल्य ‘मध्यिका’ होता है।”

मध्यिका के गुण

• यह बहुत सरल है और इसको बड़ी सुगमता से समझा जा सकता है।
• इसका निर्धारण निश्चित और शुद्ध होता है।
• इसे पदों की कुल संख्या मात्र से ज्ञात किया जा सकता है।
• मध्यिका को बिन्दु रेखाओं द्वारा प्रदर्शित किया जा सकता है।
• मध्यिका पर चरम मूल्यों का कोई प्रभाव नहीं पड़ता।
• माध्य विचलन की गणना में मध्यिका का और अधिक बीजीय विवेचन सम्भव है।
• गुणात्मक विशेषताओं को अध्ययन करने में यह अन्य माध्यों से श्रेष्ठ है।
• मध्यिका से पदों के विचलनों का योग अन्य किसी भी विधि से निकाले गए विचलनों के योग से कम होता है।

मध्यिका के दोष या सीमाएँ

• मध्यिका के पदों की संख्या से गुणा करने पर पदों का कुल योग मालूम नहीं होता।
• यदि पदों के विस्तार में असाधारण भिन्नता हो तो यह भ्रामक निष्कर्ष देता है।
• इसे ज्ञात करने के लिए समस्त पदों को आरोही (ascending) या अवरोही (descending) क्रम में व्यवस्थित करना पड़ता है।
• इसको ज्ञात करने के लिए समस्त समंकों का प्रयोग नहीं होता।
• यदि मध्यपद दो वर्गों के बीच आता है, तो मध्यिका को ठीक-ठीक ज्ञात करना कठिन हो जाता है।
• सरल गणितीय सूत्रे से इसका अनुमान नहीं लगाया जा सकता।
• यदि पदों की संख्या सम (even) है तो मध्यिका वास्तविक मूल्य नहीं होता।
• यदि पदों की संख्या कम हो या मध्य पद के ऊपर अथवा नीचे पदों का फैलाव अनियमित हो तो मध्यिका एक प्रतिनिधि माप नहीं रहता।

मध्यिका के उपयोग

मध्यिका समझने में सरल है; अत: व्यावहारिक उद्देश्यों के लिए इसका बहुत अधिक उपयोग होता है। इसके द्वारा गुणात्मक तथ्यों जैसे बुद्धिमत्ता, स्वास्थ्य आदि का भी अध्ययन किया जा सकता है। इसी कारण सामाजिक समस्याओं के विश्लेषण में यह अत्यधिक उपयोगी है। यह उन दशाओं में अधिक उपयोगी है, जहाँ अति सीमान्त पदों को महत्त्व नहीं दिया जाता अथवा वितरण विषम होता है।\

प्रश्न 5.

विभाजन मूल्य चतुर्थकों (Qi , Qs) की गणना प्रक्रिया समझाइए।

उत्तर :

किसी श्रृंखला को दो से अधिक भागों में बाँटने वाले मूल्य को विभाजन मूल्य कहते हैं। मध्यिका एक श्रेणी को दो भागों में बाँटती है। यदि किसी श्रृंखला को चार बराबर भागों में बाँटा जाता है। तो प्रत्येक भाग की अन्तिम इकाई चतुर्थक (Quartile) कहलाती है। इसे अंग्रेजी भाषा के Q अक्षर द्वारा प्रकट किया जाता है। पहले चतुर्थक की प्रथम अथवा निम्न चतुर्थक’ Q), तीसरे चतुर्थक को उच्च चतुर्थक (Q3) कहते हैं। दूसरा चतुर्थक मध्यिका कहलाता है।

चतुर्थकों की गणन क्रिया

व्यक्तिगत व खण्डित श्रेणी में – इन शृंखलाओं में चतुर्थक मूल्य ज्ञात करने के लिए निम्नांकित सूत्रों का प्रयोग किया जाता है

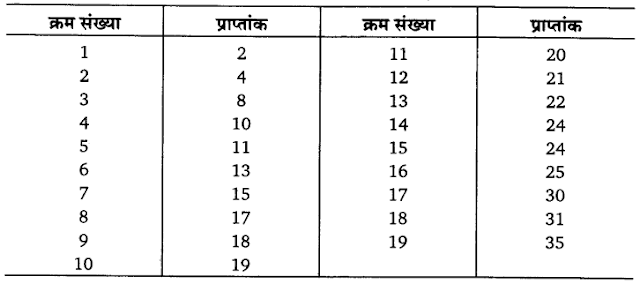
उदाहरण 8. विद्यार्थियों द्वारा सांख्यिकी में प्राप्तांक निम्नलिखित हैं18, 10, 4, 31, 25, 20, 24, 17, 35, 15, 2, 8, 19, 21, 11, 13, 22, 24, 30 उपर्युक्त में Q व Qs ज्ञात कीजिए।

उत्तर :

सर्वप्रथम, प्राप्तांकों को आरोही क्रम में व्यवस्थित किया जाएगा

उदाहरण 9. निम्नलिखित समंकों से Q व Qs ज्ञात कीजिए

उत्तर :

अखण्डित अथवा अविच्छिन्न श्रेणी – अखण्डित श्रेणी में Q; तथा Q5 के आकार को निम्नलिखित सूत्रों की सहायता से ज्ञात किया जाता है|

फिर निम्नलिखित सूत्र की सहायता से इनका मान ज्ञात किया जाता है

उदाहरण 10. निम्नलिखित समंकमाला में Q व Qs ज्ञात कीजिए

उत्तर :

प्रश्न 6.

बहुलक (भूयिष्ठक) को परिभाषित कीजिए। इसके गुण व दोष बताइए।

उत्तर :

बहुलक या भूयिष्ठक का अर्थ एवं परिभाषाएँ

किसी भी समंकमाला में जो पद सबसे अधिक बार आता है अथवा जिसकी आवृत्ति सबसे अधिक होती है, वही ‘बहुलक’ कहलाता है। यह ‘सर्वाधिक घनत्व की स्थिति का द्योतक है और इसे प्रायः मूल्यों के ‘अधिकतम संकेन्द्रण का बिन्दु’ भी कहते हैं। काउडेन के शब्दों में-“एक वितरण को बहुलक वह मूल्य है, जिसके निकट श्रेणी की इकाइयाँ अधिक-से-अधिक केन्द्रित होती हैं। उसे मूल्यों की श्रेणी का सबसे अधिक प्रतिरूपी माना जाता है।” जिजेक के अनुसार-“बहुलक वह मूल्य है, जो पदों की श्रेणी अथवा समूह में सबसे अधिक बार

आता है तथा जिसके चारों ओर सबसे अधिक घनत्व के पदों का वितरण रहता है।” कैने तथा कीपिंग के अनुसार-“बहुलक वह मूल्य है जो श्रेणी में सबसे अधिक बार आता हो अर्थात् जिसँकी सर्वाधिक आवृत्ति हो।” डॉ० बाउले के अनुसार–‘किसी सांख्यिकीय समूह में वर्गीकृत मात्रा का वह मूल्य, जहाँ पर पंजीकृत संख्याएँ सबसे अधिक हों, ‘बहुलक’ या ‘सबसे अधिक घनत्व का स्थान’ अथवा ‘सबसे महत्त्वपूर्ण मूल्य’ कहलाता है।”

बहुलक के गुण

• यह एक सरल एवं लोकप्रिय माध्य है। कुछ दशाओं में यह केवल निरीक्षण द्वारा ही ज्ञात किया जा सकता है।
• इसका मूल्य रेखाचित्र द्वारा भी निर्धारित किया जा सकता है।
• यह वितरण में सर्वाधिक सम्भावित मूल्य होता है।
• गुणात्मक तथ्यों का भी बहुलक ज्ञात किया जा सकता है।
• यह अति सीमान्त पदों से प्रभावित नहीं होता।
• यह श्रेणी के एक महत्त्वपूर्ण भाग का वास्तविक मूल्य होता है।
• यह समूह का सर्वोत्तम प्रतिनिधि होता है।
• प्रतिदर्श के परिवर्तन के साथ बहुलक में परिवर्तन नहीं होता।

बहुलक के दोष

• यदि श्रेणी के सभी पदों की आवृत्तियाँ समान हैं तो बहुलक का निर्धारण नहीं किया जा सकता।
• कभी-कभी एक समूह में दो-या-दो से अधिक बहुलक भी हो सकते हैं।
• यदि श्रेणी का वितरण अनियमित है तो इसे शुद्ध रूप में नहीं निकाला जा सकता।
• यह चरम सीमाओं की उपेक्षा करता है जो कि गणितीय दृष्टि से उचित नहीं है।
• सभी पदों पर आधारित न होने के कारण इसका बीजीय विवेचन सम्भव नहीं है।
• यह श्रेणी का पूर्ण रूप से प्रतिनिधित्व नहीं करता।
• वर्ग विस्तार में परिवर्तन कर देने पर बहुलक भी बदल जाएगा।

बहुलक के उपयोग

उपर्युक्त दोषों के बावजूद दैनिक जीवन तथा व्यापारिक क्षेत्र में बहुलक का बहुत अधिक उपयोग किया जाता है। यह शीघ्रता व सरलता से समझ में आ जाता है, इसलिए व्यावसायिक जीवन में इसका प्रयोग दिन-प्रतिदिन बढ़ता जा रहा है। व्यापारिक पूर्वानुमानों में यह एक महत्त्वपूर्ण पथ-प्रदर्शक है। उद्योग व प्रशासन के क्षेत्र में इसकी सहायता से औसत उत्पादने ज्ञात किया जाता है तथा विभिन्न विभागों की कार्यक्षमता की तुलना की जाती है। किसी वस्तु के उत्पादन में उसकी लागत का अनुमान बहुलक समय के निर्धारण द्वारा आसानी से लगाया जा सकता है। विभिन्न वस्तुओं की लोकप्रियता का अध्ययन बहुलक द्वारा ही किया जाता हैं मौसम सम्बन्धी पूर्वानुमानों में भी इसी का प्रयोग होता है।

प्रश्न 7.

बहुलक निर्धारण की विधि समझाइए।

उत्तर :

बहुलक का निर्धारण

(अ) व्यक्तिगत श्रेणी – व्यक्तिगत श्रेणी में बहुलक निकालने की निम्नलिखित विधियाँ हैं|

(i) निरीक्षण द्वारा – निरीक्षण द्वारा यह निश्चित किया जाता है कि कौन-सा मूल्य सबसे अधिक बार आया है। जो मूल्य सबसे अधिक बार आता है, वही बहुलक होता है।

उदाहरण 11. निम्नांकित जूतों की आकार संख्या से बहुलक आकार ज्ञात कीजिए

जूतों की आकार संख्या – 2, 4, 1, 2, 7, 7, 6, 6, 6, 5, 4, 2, 6, 6, 6, 3, 3

उत्तर :

उपर्युक्त संख्याओं में 6 संख्या सबसे अधिक बार प्रयुक्त हुई है। अत: यही संख्या बहुलक होगी।

z = 6 यहाँ  Z = बहुलक

(ii) व्यक्तिगत श्रेणी को खण्डित श्रेणी में परिवर्तित करके – जब व्यक्तिगत श्रेणी के अनेक पद दो-या-दो से अधिक बार आते हैं तो उन्हें आरोही क्रम में रखकर उनके सामने उनकी आवृत्ति लिख दी जाती है। सर्वाधिक आवृत्ति वाला पद बहुलक होता है।

उदाहरण 12. यदि 10 अधिकारियों को प्रारम्भिक वेतन निम्नलिखित हो तो उन अधिकारियों का बहुलक वेतन ज्ञात कीजिए

625, 500, 480, 500, 460, 500, 525, 575, 525, 500.

उत्तर :

पहले इन्हें खण्डित श्रेणी में इस प्रकार रखा जाएगा

उपर्युक्त उदाहरण में सर्वाधिक पदाधिकारियों (4) का प्रारम्भिक वेतन ₹ 500 है। अतः Z = ₹ 500

(iii) व्यक्तिगत श्रेणी को अविच्छिन्न श्रेणी में बदलकर – जब श्रेणी में किसी भी पद की आवृत्ति एक से अधिक बार नै हो, तो उसे अविच्छिन्न श्रेणी में बदलकर अधिकतम आवृत्ति वाला वर्गान्तर कर लेना चाहिए और फिर सूत्र द्वारा ‘बहुलक’ निकालना चाहिए।

नोट – इस विधि के लिए उदाहरण 21 देखिए।

(iv) मध्यिका व समान्तर माध्य के आधार पर बहुलक का निर्धारण – यदि व्यक्तिगत श्रेणी में मध्यिका व समान्तर माध्य के आधार पर बहुलक का मूल्य ज्ञात करना हो तो निम्नलिखित सूत्रे द्वारा बहुलक का मूल्य ज्ञात किया जा सकता है – z = 3 M – 2 X

(ब) खण्डित श्रेणी – खण्डित श्रेणी में बहुलक निम्नलिखित दो रीतियों द्वारा ज्ञात किया जा सकता है

(i) निरीक्षण रीति – इस रीति के अनुसार, जिस पद की सबसे अधिक आवृत्ति होगी, वही पद मूल्य ‘बहुलक’ होगा। लेकिन यह तब ही सम्भव है, जब पदमाला नियमित हो तथा उसके सभी पद सजातीय हों।

उदाहरण 13. निम्नलिखित श्रेणी में से बहुलक का आकार ज्ञात कीजिए

उदाहरण 14. निम्नलिखित सारणी में बहुलक ज्ञात कीजिए

उत्तर :

उदाहरण 14. निम्नलिखित सारणी में से बहुलक आयु ज्ञात कीजिए

उत्तर :

उपर्युक्त श्रेणी में 180 सेमी पद मूल्य की आवृत्ति सबसे अधिक है। अतः Z = 180 सेमी

(ii) समूहीकरण रीति – आवृत्तियों का वितरण अनियमित होने पर समूहन रीति द्वारा आवृत्तियों के घनत्व बिन्दु का पता लगाया जाता है। समूहन विधि इस प्रकार हैसर्वप्रथम एक सारणी बनाई जाती है, जिसमें चर मूल्यों के अतिरिक्त आवृत्ति के 6 खाने बनाए जाते हैं। इन खानों में आवृत्तियों को निम्नलिखित प्रकार से रखा जाता है

Coln. (i) में प्रश्न में दी हुई आवृत्तियाँ लिखी जाती हैं।

Coln. (ii) में आरम्भ से दो-दो आवृत्तियों के जोड़ लिखे जाते हैं।

Coln. (iii) में Coln. (i) की सबसे पहली आवृत्ति को छोड़कर, दो-दो आवृत्तियों के जोड़ लिखे जाते हैं।

Coln. (iv) में Coin. (i) की तीन-तीन आवृत्तियों के जोड़ लिखे जाते हैं।

Coln. (v) में Coln. (i) की प्रथम आवृत्ति को छोड़कर आगे की तीन-तीन आवृत्तियों के जोड़ लिखे जाते हैं।

Coln. (vi) में Coln. (i) की पहली दो आवृत्तियों को छोड़कर तीन-तीन आवृत्तियों के जोड़ लिखे जाते हैं।

इसके पश्चात् प्रत्येक कॉलम की अधिकतम आवृत्ति को रेखांकित कर लिया जाता है तथा उन अधिकतम आवृत्तियों के चर मूल्यों पर चिह्न लगाकर उनकी गणना कर ली जाती है। जिस मूल्य के सामने अधिकतम चिह्न होते हैं, वही बहुलक का मूल्य होता है। इसका विश्लेषण सारणी (Analysis table) बनाकर भी किया जा सकता है।

उदाहरण 15. निम्नलिखित सारणी में से बहुलक आयु ज्ञात कीजिए

उत्तर :

सर्वप्रथम समूहुन रीति द्वारा बहुलक वर्ग ज्ञात किया जाएगा।

उपर्युक्त सारणी के अनुसार बहुलक 40-45 वर्ग में है। सूत्रानुसार,

शून्य से भाग न दिए जा सकने के कारण, इस सूत्र द्वारा निकाला गया बहुलक शुद्ध रूप में निर्धारित नहीं किया जा सकता। अत: बहुलक मूल्य वैकल्पिक सूत्र द्वारा निर्धारित किया जाएगा। सूत्रानुसार,

एनसीईआरटी सोलूशन्स क्लास 11 Economics: Statistics for Economics (खण्ड-1 अर्थशास्त्र में सांख्यिकी)

• 1 (परिचय)
• 2 (आँकड़ों का संग्रह)
• 3 (आँकड़ों का संगठन)
• 4 (आँकड़ों का प्रस्तुतीकरण)
• 6 (परिक्षेपण के माप)
• 7 (सहसंबंध)
• 8 (सूचकांक)
• 9 (सांख्यिकीय विधियों के उपयोग)

नसीईआरटी सोलूशन्स क्लास 11 भारतीय अर्थव्यवस्था का विकास  (खण्ड -2 भारतीय अर्थव्यवस्था का विकास)

• 1 (स्वतंत्रता की पूर्व संध्या पर भारतीय अर्थव्यवस्था)
• 2 (भारतीय अर्थव्यवस्था (1950-1990))
• 3  (उदारीकरण, निजीकरण और वैश्वीकरण-एक समीक्षा)
• 4 (निर्धनता)
• 5 (भारत में मानव पूँजी का निर्माण)
• 6 (ग्रामीण विकास)
• 7 (रोजगार-संवृद्धि, अनौपचारीकरण एवं अन्य मुद्दे)
• 8 (आधारिक संरचना)
• 9 (पर्यावरण और धारणीय विकास)
• 10 (भारत और इसके पड़ोसी देशों के तुलनात्मक विकास अनुभव)