NCERT Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

Jolly April 04, 2021

NCERT Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

NCERT Solutions Class 12 भौतिकी विज्ञान-II 12 वीं कक्षा से Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति) के उत्तर मिलेंगे। यह अध्याय आपको मूल बातें सीखने में मदद करेगा और आपको इस अध्याय से अपनी परीक्षा में कम से कम एक प्रश्न की उम्मीद करनी चाहिए। 
हमने NCERT बोर्ड की टेक्सटबुक्स हिंदी  भौतिकी विज्ञान-II के सभी Questions के जवाब बड़ी ही आसान भाषा में दिए हैं जिनको समझना और याद करना Students के लिए बहुत आसान रहेगा जिस से आप अपनी परीक्षा में अच्छे नंबर से पास हो सके।
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)



सीईआरटी प्रश्न-उत्तर

Class 12 भौतिकी विज्ञान-II

पाठ-3  (विकिरण तथा द्रव्य की द्वैत प्रकृति)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1:

30 kV इलेक्ट्रॉनों के द्वारा उत्पन्न X-किरणों की
(a) उच्चतम आवृत्ति, तथा |
(b) निम्नतम तरंगदैर्ध्य प्राप्त कीजिए।
उत्तर:
दिया है, V= 30 kV = 30 x 103v
ऊर्जा E = eV = 1.6 x 10-19 x 30 x 103 J= 4.8 x 10-15 J
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 2:
सीज़ियम धातु का कार्य-फलन 2,14eV है। जब 6 x 1014 Hz आवृत्ति का प्रकाश धातु-पृष्ठ पर आपतित होता है, इलेक्ट्रॉनों का प्रकाशिक उत्सर्जन होता है।
(a) उत्सर्जित इलेक्ट्रॉनों की उच्चतम गतिज ऊर्जा
(b) निरोधी विभव, और
(c) उत्सर्जित प्रकाशिक इलेक्ट्रॉनों की उच्चतम चाल कितनी है?
उत्तर:
दिया है, सीजियम धातु का कार्य-फलन
W = 2.14 eV
= 214 x 1.6 x 10-19 जूल
आपतित प्रकाश की आवृत्ति
v = 6 x 1014 Hz
प्लांक का नियतांक
h = 6.62 x 10-34 जूल सेकण्ड
∴ आपतित फोटॉन की ऊर्जा
hν= 6.62 x 10-34 x 6 x 1014 जूल

(a) यदि उत्सर्जित प्रकाश इलेक्ट्रॉन की उच्चतम गतिज ऊर्जा Emax हो तो
आइन्सटीन के प्रकाश-विद्युत समीकरण hν = w + Emax से
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
(b) यदि विरोधी विभव V0 हो तो
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
(c) यदि उत्सर्जित प्रकाश इलेक्ट्रॉन की अधिकतम चाल νmax हो तो
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 3:
एक विशिष्ट प्रयोग में प्रकाश-विद्युत प्रभाव की अन्तक वोल्टता 1.5 v है। उत्सर्जित प्रकाशिक इलेक्ट्रॉनों की उच्चतम गतिज ऊर्जा कितनी है?
उत्तर:
संस्तब्ध वोल्टेज, V0= 1.5 V
प्रकाश इलेक्ट्रॉनों की उच्चतम गतिज ऊर्जा,
Eℜ = eV0 = 1.5 ev = 1.5 x 16 x 10-19J = 2.4 x 10-19J

प्रश्न 4:
632.8 nm तरंगदैर्घ्य का एकवर्णी प्रकाश एक हीलियम-नियॉन लेसर के द्वारा उत्पन्न किया जाता है। उत्सर्जित शक्ति 9.42mW है।
(a) प्रकाश के किरण-पुंज में प्रत्येक फोटॉन की ऊर्जा तथा संवेग प्राप्त कीजिए।
(b) इस किरण-पुंज के द्वारा विकिरित किसी लक्ष्य पर औसतन कितने फोटॉन प्रति सेकण्ड पहुँचेंगे? (यह मान लीजिए कि किरण-पुंज की अनुप्रस्थ काट एकसमान है जो लक्ष्य के
क्षेत्रफल से कम है), तथा ।
(c) एक हाइड्रोजन परमाणु को फोटॉन के बराबर संवेग प्राप्त करने के लिए कितनी तेज चाल से चलना होगा?
उत्तर:
दिया है, λ = 632.8 nm = 6328 x 10-9m
शक्ति P = 9.42 mW = 9.42 x 10-3 W
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 5:
पृथ्वी के पृष्ठ पर पहुँचने वाला सूर्यप्रकाश का ऊर्जा-अभिवाह (फ्लक्स) 1.388 x 103 W/m2 है। लगभग कितने फोटॉन प्रति वर्ग मीटर प्रति सेकण्ड पृथ्वी पर आपतित होते हैं? यह मान लें कि सूर्य-प्रकाश में फोटॉन का औसत तरंगदैर्घ्य 550nm है।
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 6:
प्रकाश-विद्युत प्रभाव के एक प्रयोग में, प्रकाश आवृत्ति के विरुद्ध अन्तक वोल्टता की ढलान 4.12 x 10-15 Vs प्राप्त होती है। प्लांक स्थिरांक का मान परिकलित कीजिए।
उत्तर:
आइन्सटीन की प्रकाश-वैद्युत समीकरण है,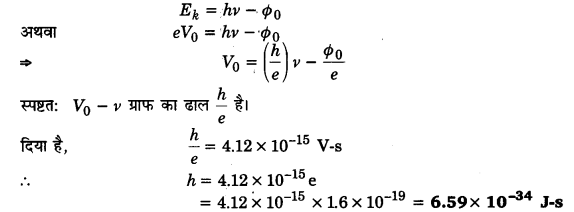
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 7:
एक 100 w सोडियम बल्ब (लैम्प) सभी दिशाओं में एकसमान ऊर्जा विकिरित करता है। लैम्प को एक ऐसे बड़े गोले के केन्द्र पर रखा गया है जो इस पर आपतित सोडियम के सम्पूर्ण प्रकाश को अवशोषित करता है। सोडियम प्रकाश का तरंगदैर्घ्य 589 nm है।
(a) सोडियम प्रकाश से जुड़े प्रति फोटॉन की ऊर्जा कितनी है?
(b) गोले को किस दर से फोटॉन प्रदान किए जा रहे हैं?
उत्तर:
दिया है, P = 100 W, λ = 589 nm = 589 x 10-9 m
(a) प्रति फोटॉन ऊर्जा,
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
(b) प्रति सेकण्ड गोले को दिए गए फोटॉनों की संख्या
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 8:
किसी धातु की देहली आवृत्ति 3.3 x 1014 Hz है। यदि 8.2 x 1014 Hz आवृत्ति का प्रकाश धातु पर आपतित हो तो प्रकाश-विद्युत उत्सर्जन के लिए अन्तक वोल्टता ज्ञात कीजिए।
उत्तर:
आइन्सटीन का प्रकाश-वैद्युत समीकरण है।
hν = hν0 + Ek
यदि अन्तक वोल्टता V% हो, तो Ek = eV0
∴ hv = hv0 +eV0
⇒ eV0 = h(ν – ν0)
= 6.63 x 10-34 (8.2 x 1014 – 3.3 x 1014)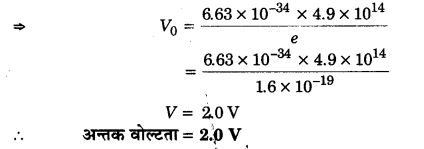
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 9:
किसी धातु के लिए कार्य-फलन 4.2eV है। क्या यह धातु 330 nm तरंगदैर्घ्य के आपतित विकिरण के लिए प्रकाश-विद्युत उत्सर्जन देगा?
उत्तर:
आपतित विकिरण के फोटॉन की ऊर्जा,
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
∴ प्रकाश धातु का कार्य-फलन, 20 = 4.2 eV (दिया है) चूँकि आपतित फोटॉन की ऊर्जा कार्य-फलन से कम है, अत: प्रकाश-इलेक्ट्रॉन उत्सर्जन सम्भव नहीं

प्रश्न 10:
7.21 x 1014 Hz आवृत्ति का प्रकाश एक धातु-पृष्ठ पर आपतित है। इस पृष्ठ से 6.0 x 10 m/s की उच्चतम गति से इलेक्ट्रॉन उत्सर्जित हो रहे हैं। इलेक्ट्रॉनों के प्रकाश उत्सर्जन के लिए देहली आवृत्ति क्या है?
उत्तर:
दिया है, आवृत्ति v = 7.21 x 1014 Hz,
νmax = 6.0 x 105 ms-1
आइन्सटीन की प्रकाश-वैद्युत समीकरण से
Ek = hν – hν0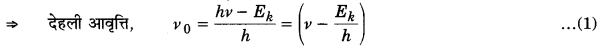
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 11:
488 pm तरंगदैर्ध्य का प्रकाश एक ऑर्गन लेसर से उत्पन्न किया जाता है, जिसे प्रकाश-विद्युत प्रभाव के उपयोग में लाया जाता है। जब इस स्पेक्ट्रमी-रेखा के प्रकाश को उत्सर्जक पर आपतित किया जाता है, तब प्रकाशिक इलेक्ट्रॉनों का निरोधी (अन्तक) विभव 0.38 V है। उत्सर्जक के पदार्थ का कार्य-फलन ज्ञात करें।
उत्तर:
दिया है, λ = 488 nm = 488 x 10-9m, V0 = 0.38 V
आपतित फोटॉन की ऊर्जा,
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 12:
56V विभवान्तर के द्वारा त्वरित इलेक्ट्रॉनों का
(a) संवेग, और
(b) डी-ब्रॉग्ली तरंगदैर्घ्य परिकलित कीजिए।
उत्तर:
इलेक्ट्रॉन का द्रव्यमान = 9.1 x 10-31 kg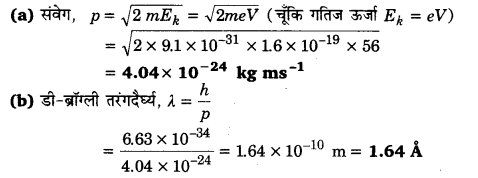
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 13:
एक इलेक्ट्रॉन जिसकी गतिज ऊर्जा 120 eV है, उसका (a) संवेग, (b) चाल, और (c) डी-ब्रॉग्ली तरंगदैर्ध्य क्या है?
उत्तर:
गतिज ऊर्जा, Ec = 120 eV = 120 x 1.6 x 10-19 J
= 1.92 x 10-17 J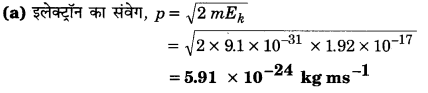
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 14:
सोडियम के स्पेक्ट्रमी उत्सर्जन रेखा के प्रकाश का तरंगदैर्घ्य 589 nm है। वह गतिज ऊर्जा ज्ञात कीजिए जिस पर
(a) एक इलेक्ट्रॉन, और
(b) एक न्यूट्रॉन का डी-ब्रॉग्ली तरंगदैर्घ्य समान होगा।
उत्तर:
दिया है, λ = 589 nm = 5.89 x 10-7m [∵1 nm = 10-9 m]
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 15:
(a) एक 0.040 kg द्रव्यमान का बुलेट जो 1.0 km/s की चाल से चल रहा है, (b) एक 0.060 kg द्रव्यमान की गेंद जो 1.0m/s की चाल से चल रही है, और (c) एक धूल-कण जिसका द्रव्यमान 1.0 x 10-9kg और जो 2.2m/s की चाल से अनुगमित हो रहा है, का डी-ब्रॉग्ली तरंगदैर्घ्य कितना होगा?
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 16:
एक इलेक्ट्रॉन और एक फोटॉन प्रत्येक का तरंगदैर्घ्य 1.00 pm है।
(a) इनका संवेग,
(b) फोटॉन की ऊर्जा, और
(c) इलेक्ट्रॉन की गतिज ऊर्जा ज्ञात कीजिए।
उत्तर:
दिया है, ∴ λ= 1.00 nm = 1.00 x 10-9m
(a) इलेक्ट्रॉन तथौ फोटॉन के संवेग होते हैं।
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
(b) फोटॉन की ऊर्जा,
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
(c) इलेक्ट्रॉन की गतिज ऊर्जा,
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 17:
(a) न्यूट्रॉन की किस गतिज ऊर्जा के लिए डी-ब्रॉग्ली तरंगदैर्घ्य 1.40 x 10-10 m होगा?
(b) एक न्यूट्रॉन, जो पदार्थ के साथ तापीय साम्य में है और जिसकी 300 K पर औसत गतिज ऊर्जा Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)kT है, का भी डी-ब्रॉग्ली तरंगदैर्घ्य ज्ञात कीजिए।
उत्तर:
(a) डी-ब्रॉग्ली तरंगदैर्घ्य,
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
(b) डी-ब्रॉग्ली तरंगदैर्घ्य,
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 18:
यह दर्शाइए कि विद्युतचुम्बकीय विकिरण का तरंगदैर्घ्य इसके क्वांटम (फोटॉन) के तरंगदैर्घ्य के बराबर है।
उत्तर:
वैद्युत-चुम्बकीय विकिरण की तरंगदैर्घ्य,
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
समीकरण (1) व (3) की तुलना करने पर, λ = λ’
अर्थात् वैद्युत-चुम्बकीय विकिरण की तरंगदैर्घ्य, डी-ब्रॉग्ली तरंगदैर्घ्य के बराबर है।

प्रश्न 19:
वायु में 300 K ताप पर एक नाइट्रोजन अणु का डी-ब्रॉग्ली तरंगदैर्घ्य कितना होगा? यह मानें कि अणु इस ताप पर अणुओं के चाल वर्ग माध्य से गतिमान है। (नाइट्रोजन का परमाणु द्रव्यमान= 14.0076 u)
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

अतिरिक्त अभ्यास

प्रश्न 20:
(a) एक निर्वात नली के तापित कैथोड से उत्सर्जित इलेक्ट्रॉनों की उस चाल का आकलन कीजिए, जिससे वे उत्सर्जक की तुलना में 500v के विभवान्तर पर रखे गए एनोड से टकराते हैं। इलेक्ट्रॉनों के लघु प्रारम्भिक चालों की उपेक्षा कर दें। इलेक्ट्रॉन का आपेक्षिक आवेश अर्थात् \frac { e }{ m }= 1.76 x 1011 C kg है।।
(b) संग्राहक विभव 10 MV के लिए इलेक्ट्रॉनों की चाल ज्ञात करने के लिए उसी सूत्र का प्रयोग करें, जो (a) में काम में लाया गया है। क्या आप इस सूत्र को गलत पाते हैं? इस सूत्र को किस प्रकार सुधारा जा सकता है?
उत्तर:
(a) त्वरक विभव V= 500 V
इलेक्ट्रॉन का आपेक्षिक आवेश Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)= 1.76 x 1011 c kg-1
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
माना एनोड से टकराते समय इलेक्ट्रॉनों का वेग ν है, तब
इलेक्ट्रॉनों की ऊर्जा में वृद्धि
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
(b) पुनः इलेक्ट्रॉन की चाल
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
∵ इलेक्ट्रॉन की यह चाल निर्वात् में प्रकाश की चाल c= 3 x 10 m s-1 से अधिक है तथा हम जानते हैं कि कोई द्रव्य कण निर्वात् में प्रकाश के वेग के बराबर अथवा अधिक चाल से नहीं चल सकता। इससे स्पष्ट है कि इस दशा में उक्त सूत्र (K. E. = \frac { 1 }{ 2 }mν2) सही नहीं हो सकता।
इस दशा में इलेक्ट्रॉन की सही चाल ज्ञात करने के लिए सापेक्षता के विशिष्ट सिद्धान्त का उपयोग करना होगा।
इस सिद्धान्त के अनुसार यदि कोई द्रव्य कण प्रकाश के वेग के तुलनीय वेग से गति करता है तो उसका गतिज द्रव्यमान निम्नलिख़ित होगा
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 21:
(a) एक समोर्जी इलेक्ट्रॉन किरण-पुंज जिसमें इलेक्ट्रॉन की चाल 5.20 x 106 ms-1 है, पर एक चुम्बकीय-क्षेत्र 1.30 x 10-4 किरण-पुंज की चाल के लम्बवत् लगाया जाता है। किरण-पुंज द्वारा आरेखित वृत्त की त्रिज्या कितनी होगी, यदि इलेक्ट्रॉन के Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)का मान 1.76 x 1011C kg-1 है।
(b) क्या जिस सूत्र को (a) में उपयोग में लाया गया है वह यहाँ भी एक 20 Mev इलेक्ट्रॉन किरण-पुंज की त्रिज्या परिकलित करने के लिए युक्तिपरक है? यदि नहीं तो किस प्रकार इसमें संशोधन किया जा सकता है? [नोट: प्रश्न 20 (b) तथा 21 (b) आपको आपेक्षिकीय यांत्रिकी तक ले जाते हैं जो पुस्तक के विषय के बाहर है। यहाँ पर इन्हें इस बिन्दु पर बल देने के लिए सम्मिलित किया गया है कि जिन सूत्रों को आप (a) में उपयोग में लाते हैं वे बहुत उच्च चालों अथवा ऊर्जाओं पर युक्तिपरक नहीं होते। यह जानने के लिए कि ‘बहुत उच्च चाल अथवा ऊर्जा का क्या अर्थ है? अन्त में दिए गए उत्तरों को देखें।
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
इलेक्ट्रॉन की चाल = 2.65 x 109 m/s
∵ इलेक्ट्रॉन की चाल निर्वात् में प्रकाश की चाल से अधिक है। अतः पथ की त्रिज्या का परिकलन करने के लिए सामान्य सूत्र का प्रयोग नहीं किया जा सकता अपितु आपेक्षिकीय यांत्रिकी का प्रयोग करना होगा।
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
उक्त सूत्र से पथ की त्रिज्या की गणना की जा सकती है।

प्रश्न 22:
एक इलेक्ट्रॉन गन जिसका संग्राहक 100V विभव पर है, एक कम दाब (~10-2 mm Hg) पर हाइड्रोजन से भरे गोलाकार बल्ब में इलेक्ट्रॉन छोड़ती है। एक चुम्बकीय-क्षेत्र जिसका मान 2.83 x 10-4 Tहै, इलेक्ट्रॉन के मार्ग को 12.0 cm त्रिज्या के वृत्तीय कक्षा में वक्रित कर देता है। (इस मार्ग को देखा जा सकता है क्योंकि मार्ग में गैस आयन किरण-पुंज को इलेक्ट्रॉनों को आकर्षित करके और इलेक्ट्रॉन प्रग्रहण के द्वारा प्रकाश उत्सर्जन करके फोकस करते हैं; इस विधि को परिष्कृत किरण-पुंज नली विधि कहते हैं। आँकड़ों से Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)का मान निर्धारित कीजिए।
उत्तर:
दिया है, इलेक्ट्रॉनों के लिए त्वरक विभव V = 100 V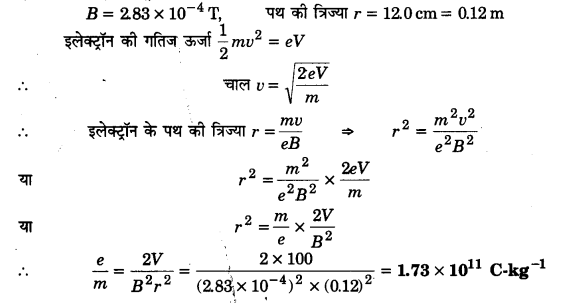
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 23:
(a) एक x-किरण नली विकिरण का एक संतत स्पेक्ट्रम जिसका लघु तरंगदैर्घ्य सिरा 0.45 Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)पर है, उत्पन्न करता है। विकिरण में किसी फोटॉन की उच्चतम ऊर्जा कितनी है? (b) अपने (a) के उत्तर से अनुमान लगाइए कि किस कोटि की त्वरक वोल्टता (इलेक्ट्रॉन के लिए) की इस नली में आवश्यकता है?
उत्तर:
(a) X – किरण विकिरण में λ = 0.45 Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)= 45 x 10-12 m
∴ विकिरण में फोटॉन की उच्चतम ऊर्जा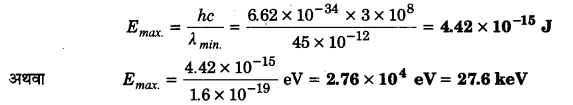
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
(b) माना लक्ष्य से टकराने वाले इलेक्ट्रॉनों को उक्त ऊर्जा प्रदान करने के लिए त्वरक विभव V की आवश्यकता होती है।
तब इलेक्ट्रॉन की ऊर्जा E = eV
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 24:
एक त्वरित्र (accelerator) प्रयोग में पॉजिट्रॉनों (e+) के साथ इलेक्ट्रॉनों के उच्च-ऊर्जा संघट्टन पर, एक विशिष्ट घटना की व्याख्या कुल ऊर्जा 10.2 BeV के इलेक्ट्रॉन-पॉजिट्रॉन युग्म के बराबर ऊर्जा की दो γ-किरणों में विलोपन के रूप में की जाती है। प्रत्येक γ-किरण से सम्बन्धित तरंगदैघ्र्यों के मान क्या होंगे? (1 BeV= 109 eV)
उत्तर:
घटना में विलुप्त इलेक्ट्रॉन-पॉजिट्रॉन की कुल ऊर्जा = 10.2 x 109 eV
यह ऊर्जा दोनों γ-फोटॉनों में बराबर-बराबर बँट जाएगी।
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 25:
आगे आने वाली दो संख्याओं का आकलन रोचक हो सकता है। पहली संख्या यह बताएगी कि रेडियो अभियान्त्रिक फोटॉन की अधिक चिन्ता क्यों नहीं करते। दूसरी संख्या आपको यह बताएगी कि हमारे नेत्र ‘फोटॉनों की गिनती क्यों नहीं कर सकते, भले | ही प्रकाश साफ-साफ संसूचन योग्य हो।
(a) एक मध्य तरंग (medium wave) 10 kW सामर्थ्य के प्रेषी, जो 500 m तरंगदैर्ध्य की रेडियो तरंग उत्सर्जित करता है, के द्वारा प्रति सेकण्ड उत्सर्जित फोटॉनों की संख्या।
(b) निम्नतम तीव्रता का श्वेत प्रकाश जिसे हम देख सकते हैं (10-10 w m4) के संगत फोटॉनों की संख्या जो प्रति सेकण्ड हमारे नेत्रों की पुतली में प्रवेश करती है। पुतली का क्षेत्रफल लगभग 0.4 cm और श्वेत प्रकाश की औसत आवृत्ति को लगभग 6 x 1024 Hz मानिए।
उत्तर:
(a) प्रेषी की शक्ति P = 10 kW = 104 W
उत्सर्जित फोटॉनों की तरंगदैर्घ्य λ = 500 m
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
हम देख सकते हैं कि 10 kW सामर्थ्य के प्रेषी द्वारा प्रति सेकण्ड उत्सर्जित फोटॉनों की संख्या इतनी अधिक है। अत: फोटॉनों की अलग-अलग ऊर्जा की उपेक्षा करके रेडियो तरंगों की कुल ऊर्जा को सतत माना जा सकता है।

(b) श्वेत प्रकाश की औसत आवृत्ति v = 6 x 104 Hz
∴ श्वेत प्रकाश की फोटॉन की ऊर्जा E = hav = 6.62 x 10-34 x 6 x 1014
= 3.97 x 10-19 J
आँख द्वारा संसूचित न्यूनतम तीव्रता = 10-10 Wm-2
इस स्थिति में आँख में प्रवेश करने वाले प्रकाश की न्यूनतम शक्ति
P = 10-10 Wm-2 x (0.4 x 10-4 m2)
= 4 x 10415 W
∴ आँख में प्रति सेकण्ड प्रवेश करने वाले फोटॉनों की संख्या
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
यद्यपि यह संख्या रेडियो प्रेषी द्वारा प्रति सेकण्ड उत्सर्जित फोटॉनों की संख्या से अत्यन्त कम है। परन्तु आँख के सूक्ष्म क्षेत्रफल की दृष्टि से इतनी अधिक है कि हम आँख पर गिरने वाले फोटॉनों के अलग-अलग प्रभाव को संसूचित नहीं कर पाते अपितु प्रकाश के सतत प्रभाव का अनुभव करते हैं।

प्रश्न 26:
एक 100 W पारद (Mercury) स्रोत से उत्पन्न 2271 Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)तरंगदैर्घ्य का पराबैंगनी प्रकाश एक मॉलिब्डेनम धातु से निर्मित प्रकाश सेल को विकिरित करता है। यदि निरोधी विभव – 1.3 V हो तो धातु के कार्य-फलन का आकलन कीजिए। एक He-Ne लेसर द्वारा . उत्पन्न 6328 Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)के उच्च तीव्रता (~105 w m-2) के लाल प्रकाश के साथ प्रकाश सेल
किस प्रकार अनुक्रिया करेगा?
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 27:
एक नियॉन लैम्प से उत्पन्न 640.2nm (1 nm = 10-9 m) तरंगदैर्ध्य का एकवर्णी विकिरण टंगस्टन पर सीजियम से निर्मित प्रकाश-संवेदी पदार्थ को विकिरित करता है। निरोधी वोल्टता 0.54 V मापी जाती है। स्रोत को एक लौह-स्रोत से बदल दिया जाता है। इसकी 427.2 nm वर्ण-रेखा उसी प्रकाश सेल को विकिरित करती है। नयी निरोधी वोल्टता ज्ञात कीजिए।
उत्तर:
दिया है, λ1 = 640.2nm = 640.2 x 10-9 m
निरोधी वोल्टता V1 = 0.54 V
λ2 = 427.2nm = 427.2 x 10-9m के लिए निरोधी विभव V2 = ?
आइन्स्टीन के प्रकाश-विद्युत समीकरण से,
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 28:
एक पारद लैम्प, प्रकाश-विद्युत उत्सर्जन की आवृत्ति निर्भरता के अध्ययन के लिए एक सुविधाजनक स्रोत है, क्योंकि यह दृश्य-स्पेक्ट्रम के पराबैंगनी (UV) से लाल छोर तक कई वर्ण-रेखाएँ उत्सर्जित करता है। रूबीडियम प्रकाश सेल के हमारे प्रयोग में, पारद (Mercury) स्रोत की निम्न वर्ण-रेखाओं का प्रयोग किया गया
λ1 = 3650Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति),
λ2 = 4047Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति),
λ3 = 4358Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति),
λ4 = 5461A, 25 = 6907Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
निरोधी वोल्टताएँ, क्रमशः निम्न मापी गईं हैं
V01 = 1.28 v,
V02 = 0.95 v,
V03 = 0.74V,
V04 = 0.16 V,
V05 = 0V
(a) प्लांक स्थिरांक h का मान ज्ञात कीजिए।
(b) धातु के लिए देहली आवृत्ति तथा कार्य-फलन का आकलन कीजिए।
[नोट-उपर्युक्त आँकड़ों से h का मान ज्ञात करने के लिए आपको e = 1.6 x 10-19 C की आवश्यकता होगी। इस प्रकार के प्रयोग Na,Li, K आदि के लिए मिलिकन ने किए थे। मिलिकन ने अपने तेल-बूंद प्रयोग से प्राप्त के मान का उपयोग कर आइन्स्टीन के प्रकाश विद्युत समीकरण को सत्यापित किया तथा इन्हीं प्रेक्षणों से h के मान के लिए पृथक् अनुमान लगाया।]
उत्तर:
किसी दी गई तरंगदैर्घ्य 2 के लिए संगत आवृत्ति
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 29:
कुछ धातुओं के कार्य-फलन निम्न प्रकार दिए गए हैं
Na: 2.75 ev; K: 2.30 ev; Mo:417ev; Ni : 5.15 ev इनमें धातुओं में से कौन प्रकाश सेल से 1m दूर रखे गए He-cd लेसर से उत्पन्न 3300Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)तरंगदैर्घ्य के विकिरण के लिए प्रकाश-विद्युत उत्सर्जन नहीं देगा? लेसर को सेल के निकट 50 cm दूरी पर रखने पर क्या होगा?
उत्तर:
He-Cd लेसर से उत्पन्न तरंगदैर्घ्य λ = 3300Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)= 3.3 x 10-7m
इस विकिरण के एक फोटॉन की ऊर्जा
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
∵ Mo तथा Ni के लिए कार्य-फलंन, उक्त विकिरण के एक फोटॉन की ऊर्जा से अधिक है; अतः उक्त दोनों धातु प्रकाश-विद्युत उत्सर्जन नहीं देंगे। यदि लेसर को 1m के स्थान पर 50 cm दूरी पर रख दें तो भी उक्त परिणाम में कोई अन्तर नहीं आएगा, क्योंकि लेसर को समीप रखने पर धातु पर गिरने वाले प्रकाश की तीव्रता तो बढ़ जाएगी,परन्तु एक फोटॉन से सम्बद्ध ऊर्जा में कोई परिवर्तन नहीं होगा।

प्रश्न 30:
10-5 W m-2 तीव्रता का प्रकाश सोडियम प्रकाश सेल के 2 cm2 क्षेत्रफल के पृष्ठ पर पड़ता है। यह मान लें कि ऊपर की सोडियम की पाँच परतें आपतित ऊर्जा को अवशोषित करती हैं तो विकिरण के तरंग-चित्रण में प्रकाश-विद्युत उत्सर्जन के लिए आवश्यक समय का आकलन कीजिए। धातु के लिए कार्य-फलन लगभग 2eV दिया गया है। आपके उत्तर का क्या निहितार्थ है?
उत्तर:
दिया है, प्रकाश की तीव्रता I = 10-5 W/m2
सेल का क्षेत्रफल A= 2 x 10-4m, कार्य-फलन Φ0 = 2eV
∴ सोडियम परमाणु की लगभग त्रिज्या r = 10-10 m
∴ सोडियम परमाणु का लगभग क्षेत्रफल πr² = 3.14 x 10-20 = 10-20 m2
∴ एक परत में उपस्थित सोडियम परमाणुओं की संख्या
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
∴ 5 परतों में परमाणुओं की संख्या n= 5 x 2x 1016 = 1017
∵ सोडियम के एक परमाणु में एक चालन इलेक्ट्रॉन होता है; अतः इन n परमाणुओं में n चालन इलेक्ट्रॉन होंगे। सेल पर प्रति सेकण्ड आपतित प्रकाशिक ऊर्जा = I x A
= 10-5 x 2 x 10-4 = 2x 109W
∵ कुल ऊर्जा.सोडियम की पाँच परतों द्वारा अवशोषित होती है; अतः तरंग सिद्धान्त के अनुसार यह ऊर्जा पाँच परतों के n. इलेक्ट्रॉनों में समान रूप से बँट जाती है।
∴ एक इलेक्ट्रॉन को प्रति सेकण्ड प्राप्त होने वाली ऊर्जा
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
अर्थात् 1 इलेक्ट्रॉन को उत्सर्जित कराने के लिए आवश्यक ऊर्जा = 3.2 x 10-19 J
∴ किसी इलेक्ट्रॉन को उत्सर्जित होने में लगा समय है = पर्याप्त ऊर्जा प्राप्त करने में लगा समय
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
उत्तर का निहितार्थ: इस उत्तर से स्पष्ट है कि प्रकाश के तरंग सिद्धान्त के अनुसार प्रकाश विद्युत-उत्सर्जन की घटना में एक इलेक्ट्रॉन को उत्सर्जित होने में लगने वाला समय बहुत अधिक है जो कि इलेक्ट्रॉन उत्सर्जन में लगे प्रेक्षित समय (लगभग 10-9s) से मेल नहीं खाता। इससे स्पष्ट है कि प्रकाश का तरंग सिद्धान्त प्रकाश विद्युत उत्सर्जन की व्याख्या नहीं कर सकता।

प्रश्न 31:
X-किरणों के प्रयोग अथवा उपयुक्त वोल्टता से त्वरित इलेक्ट्रॉनों से क्रिस्टल-विवर्तन प्रयोग किए जा सकते हैं। कौन-सी जाँच अधिक ऊर्जा सम्बद्ध है? (परिमाणिक तुलना के लिए, जाँच के लिए तरंगदैर्घ्य को 1Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)लीजिए, जो कि जालक (लेटिस) में अन्तर-परमाणु अन्तरण की कोटि को है) (me = 9.11 x 10-31 kg)।
उत्तर:
दिया है, X-किरण फोटॉन तथा इलेक्ट्रॉन की तरंगदैर्घ्य λ = 1Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)= 10-10 m
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 32:
(a) एक न्यूट्रॉन, जिसकी गतिज ऊर्जा 150 eV है, का डी-ब्रॉग्ली तरंगदैर्घ्य प्राप्त कीजिए। जैसा कि आपने प्रश्न 31 में देखा है, इतनी ऊर्जा का इलेक्ट्रॉन किरण-पुंज क्रिस्टल विवर्तन प्रयोग के लिए उपयुक्त है। क्या समान ऊर्जा का एक न्यूट्रॉन किरण-पुंज इस प्रयोग
के लिए समान रूप से उपयुक्त होगा? स्पष्ट कीजिए। [mn = 1.675 x 10-27 kg]
(b) कमरे के सामान्य ताप (27°C) पर ऊष्मीय न्यूट्रॉन से जुड़े डी-ब्रॉग्ली तरंगदैर्घ्य ज्ञात कीजिए। इस प्रकार स्पष्ट कीजिए कि क्यों एक तीव्रगामी न्यूट्रॉन को न्यूट्रॉन-विवर्तन प्रयोग में उपयोग में लाने से पहले वातावरण के साथ तापीकृत किया जाता है।
उत्तर:
(a) दिया है, न्यूट्रॉन की ऊर्जा E = 150 eV = 150 x 1.6 x 10-19 J.
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

(b) दिया है, कमरे का तापमान T = 27 + 273 = 300K
न्यूट्रॉन का द्रव्यमान mn = 1.675 x 10-27 kg
बोल्टजमैन नियतांक k = 1.38 x 10-23 J/mole K
कमरे के ताप पर न्यूट्रॉन की गतिज ऊर्जा
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
स्पष्ट है कि 27°C के न्यूट्रॉन की डी-ब्रॉग्ली तरंगदैर्घ्य, क्रिस्टलों में अन्तरापरमाण्विक दूरी के साथ तुलनीय है। अतः यह न्यूट्रॉन क्रिस्टल विवर्तन प्रयोग के लिए उपयुक्त है। इससे स्पष्ट है कि न्यूट्रॉनों को क्रिस्टल विवर्तन प्रयोगों में उपयोग में लाने के लिए उन्हें वातावरण के साथ तापीकृत करना चाहिए।

प्रश्न 33:
एक इलेक्ट्रॉन सूक्ष्मदर्शी में 50 kV वोल्टता के द्वारा त्वरित इलेक्ट्रॉनों का उपयोग किया जाता है। इन इलेक्ट्रॉनों से जुड़े डी-ब्रॉग्ली तरंगदैर्घ्य ज्ञात कीजिए। यदि अन्य बातों (जैसे कि संख्यात्मक द्वारक आदि) को लगभग समान लिया जाए, इलेक्ट्रॉन सूक्ष्मदर्शी की विभेदन क्षमता की तुलना पीले प्रकाश का प्रयोग करने वाले प्रकाश सूक्ष्मदर्शी से किस प्रकार होती है?
उत्तर:
दिया है, इलेक्ट्रॉनों का त्वरक विभवान्तर V= 50kV= 50 x 103 v
∴ इलेक्ट्रॉन की ऊर्जा E = eV जूल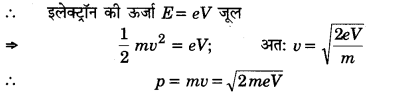
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 34:
किसी जाँच की तरंगदैर्घ्य उसके द्वारा कुछ विस्तार में जाँच की जा सकने वाली संरचना के आकार की लगभग आमाप है। प्रोटॉनों तथा न्यूट्रॉनों की क्वार्क (quark) संरचना 10-15 m या इससे भी कम लम्बाई के लघु पैमाने की है। इस संरचना को सर्वप्रथम 1970 दशक के प्रारम्भ में, एक रेखीय त्वरित्र (Linear accelerator) से उत्पन्न उच्च ऊर्जा इलेक्ट्रॉनों के किरणे-पुंजों के उपयोग द्वारा, स्टैनफोर्ड, संयुक्त राज्य अमेरिका में जाँचा गया था। इन इलेक्ट्रॉन किरण-पुंजों की ऊर्जा की कोटि का अनुमान लगाइए। (इलेक्ट्रॉन
की विराम द्रव्यमान ऊर्जा 0.511 MeV है।)
उत्तर:
क्वार्क संरचना का आमाप, λ = 10-15m
इलेक्ट्रॉन का विराम द्रव्यमान m0 = 9.1 x 10-31 kg
∴ इलेक्ट्रॉन की विराम द्रव्यमान ऊर्जा ।
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 35:
कमरे के ताप (27°C) और 1 atm दाब पर He परमाणु से जुड़े प्रारूपी डी-ब्रॉग्ली तरंगदैर्घ्य ज्ञात कीजिए और इन परिस्थितियों में इसकी तुलना दो परमाणुओं के बीच औसत दूरी से कीजिए।
उत्तर:

कमरे का ताप T = 27 + 273 = 300 K 

He का परमाणु द्रव्यमान = 4g

Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 36:
किसी धातु में (27°C) पर एक इलेक्ट्रॉन का प्रारूपी डी-ब्रॉग्ली तरंगदैर्घ्य परिकलित कीजिए और इसकी तुलना धातु में दो इलेक्ट्रॉनों के बीच औसत पृथक्य से कीजिए जो लगभग 2 x 10-10 m दिया गया है। (नोट-प्रश्न 35 और 36 प्रदर्शित करते हैं कि जहाँ सामान्य परिस्थितियों में गैसीय अणुओं से जुड़े तरंग पैकेट अ-अतिव्यापी हैं; किसी धातु में इलेक्ट्रॉन तरंग पैकेट प्रबल रूप से एक-दूसरे से अतिव्यापी हैं। यह सुझाता है कि जहाँ किसी सामान्य गैस में अणुओं की अलग पहचान हो सकती है, किसी धातु में । इलेक्ट्रॉन की एक-दूसरे से अलग पहचान नहीं हो सकती। इस अप्रभेद्यता के कई मूल निहितार्थताएँ हैं। जिन्हें आप भौतिकी के अधिक उच्च पाठ्यक्रमों में जानेंगे]
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 37:
निम्नलिखित प्रश्नों के उत्तर दीजिए
(a) ऐसा विचार किया गया है कि प्रोटॉन और न्यूट्रॉन के भीतर क्वार्क पर आंशिक आवेश होते
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
यह मिलिकन तेल-बूंद प्रयोग में क्यों नहीं प्रकट होते?
(b) संयोग की क्या विशिष्टता है? हम e तथाm के विषय में अलग-अलग विचार क्यों नहीं करते?
(c) गैसें सामान्य दाब पर कुचालक होती हैं, परन्तु बहुत कम दाब पर चालन प्रारम्भ कर देती हैं। क्यों?
(d) प्रत्येक धातु का एक निश्चित कार्य-फलन होता है। यदि आपतित विकिरण एकवर्णी हो तो सभी प्रकाशिक इलेक्ट्रॉन समान ऊर्जा के साथ बाहर क्यों नहीं आते हैं? प्रकाशिक इलेक्ट्रॉनों का एक ऊर्जा वितरण क्यों होता है?
(e) एक इलेक्ट्रॉन की ऊर्जा तथा इसका संवेग इससे जुड़े पदार्थ-तरंग की आवृत्ति तथा इसके तरंगदैर्घ्य के साथ निम्न प्रकार सम्बन्धित होते हैं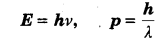
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
परन्तु λ का मान जहाँ भौतिक महत्त्व का है, के मान (और इसलिए कला चाल 22 को मान) का कोई भौतिक महत्त्व नहीं है। क्यों?
उत्तर:
(a) भिन्नात्मक आवेश वाले क्वार्क न्यूट्रॉन तथा प्रोटॉन के भीतर इस प्रकार सीमित रहते हैं कि प्रोटॉन में उपस्थित क्वार्को के आवेशों का योग +e तथा न्यूट्रॉन में उपस्थित क्वार्को के आवेशों का योग । शून्य बना रहता है तथा ये क्वार्क पारस्परिक आकर्षण बलों द्वारा बँधे रहते हैं। जब इन्हें अलग करने का प्रयास किया जाता है तो बल और अधिक शक्तिशाली हो जाते हैं और इसी कारण वे एक साथ बने रहते हैं। इसीलिए प्रकृति में भिन्नात्मक आवेश मुक्त अवस्था में नहीं पाए जाते अपितु वे सदैव इलेक्ट्रॉनिक आवेश के पूर्ण गुणज के रूप में ही पाए जाते हैं।

(b) इलेक्ट्रॉन की गति समीकरणों eV= Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)mν, eE = ma तथा eνB = mν2/r द्वारा निर्धारित होती है। इनमें से प्रत्येक में e तथा m दोनों एक साथ आए हैं। इससे स्पष्ट है कि इलेक्ट्रॉन की गति के लिए e अथवा m पर अकेले-अकेले विचार करने के स्थान पर \frac { e }{ m }पर विचार किया जाता है।

(c) सामान्य दाब पर गैसों में विसर्जन के कारण उत्पन्न आयन कुछ ही दूरी तय करने तक गैस के
अन्य अणुओं से टकराकर उदासीन हो जाते हैं और इस कारण सामान्य दाब पर गैसों में विद्युत चालन नहीं हो पाता। इसके विपरीत अत्यन्त निम्न दाब पर गैस में अणुओं की संख्या बहुत कम रह जाती है। इस कारण उत्पन्न आयन अन्य अणुओं से टकराने से पूर्व ही विपरीत इलेक्ट्रॉड तक पहुँच जाते हैं।

(d) कार्य फलन से, धातु में उच्चतम ऊर्जा स्तर अथवा चालन बैण्ड में उपस्थित इलेक्ट्रॉनों के उत्सर्जन के लिए आवश्यक न्यूनतम ऊर्जा का ज्ञान होता है। परन्तु प्रकाश विद्युत उत्सर्जन में । इलेक्ट्रॉन अलग-अलग ऊर्जा स्तरों से निकल कर आते हैं। अतः उत्सर्जन के बाद उनके पास , भिन्न-भिन्न ऊर्जाएँ होती हैं।

(e) किसी द्रव्य कण की ऊर्जा का निरपेक्ष मान (न कि संवेग) एक निरपेक्ष स्थिरांक के अधीन स्वेच्छ होता है। यही कारण है कि द्रव्य तरंगों से सम्बद्ध तरंगदैर्घ्य λ का ही भौतिक महत्त्व होता है न कि आवृत्ति ν का। इसी कारण कला वेग νλका भी कोई भौतिक महत्त्व नहीं होता।

परीक्षोपयोगी प्रश्नोत्तर

बहुविकल्पीय प्रश्न

प्रश्न 1:
किसी धातु का कार्य फलन  Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति) है। इसके पृष्ठ पर λ तरंगदैर्घ्य का प्रकाश आपतित होता है। धातु में से इलेक्ट्रॉन उत्सर्जन के लिए शर्त है (2015)
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
उत्तर:

(iii) λ = λ0

प्रश्न 2:
किसी धात्विक पृष्ठ से इलेक्ट्रॉन उत्सर्जन तभी सम्भव है, जब आपतित प्रकाश की आवृत्ति (2016)
(i) देहली आवृत्तिं की आधी हो।
(ii) देहली आवृत्ति की एक तिहाई हो
(iii) देहली आवृत्ति से कुछ कम हो
(iv) देहली आवृत्ति से अधिक हो।
उत्तर:
(iv) देहली आवृत्ति से अधिक हो।

प्रश्न 3:
प्रकाश वैद्युत प्रयोग में निरोधी विभव Vs तथा आपतित प्रकाश की आवृत्ति के बीच ग्राफ खींचने पर एक सरल रेखा प्राप्त होती है जो अक्ष से 8 कोण बनाती है। यदि पृष्ठ का कार्य फलन Φ हो, तो tanθ का मान होगा
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
उत्तर:
(i) Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 4:
समान गतिज ऊर्जा वाले विभिन्न कणों की डी-ब्रॉग्ली तरंगदैर्घ्य (λ), कण के द्रव्यमान पर (m) निर्भर करती है (2014)
(i) λ α m
(ii) λ α m1/2
(iii) λ α m-1
(iv) λ α m-1/2
उत्तर:
(iv) λ α m-1/2

प्रश्न 5:
किसी गतिमान कण से सम्बद्ध डी-ब्रॉग्ली तरंग की तरंगदैर्घ्य निर्भर नहीं करती है (2011, 16)
(i) द्रव्यमान पर
(ii) आवेश पर
(iii) वेग पर
(iv) संवेग पर
उत्तर:
(ii) आवेश पर

प्रश्न 6:
यदि किसी कण का संवेग दुगुना कर दिया जाए, तो इसकी डी-ब्रॉग्ली तरंगदैर्घ्य होगी (2017)
(i) अपरिवर्तित
(i) चारगुनी
(iii) दुगुनी
(iv) आधी
उत्तर:
(iv) आधी

प्रश्न 7:
फोटॉन.का विराम द्रव्यमान होता है
(i) E/c2
(ii) h/cλ
(iii) h/λ
(iv) शून्य
उत्तर:
(iv) शून्य

प्रश्न 8:
फोटॉन के गतिक द्रव्यमान का सूत्र है (2009)
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 9:
फोटॉन के गतिज द्रव्यमान का सूत्र है (2015, 17)
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
जहाँ, h प्लांक नियतांक, ν फोटॉन की आवृत्ति तथा c उसकी चाल है
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 10:
एक फोटॉन की तरंगदैर्घ्य 1Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)है। इसका संवेग होगा : (2011)
(i) 0.1 h
(ii) 10h
(iii) 1010h
(iv) 1011h
उत्तर:
(iii) 1010h

अतिलघु उत्तरीय प्रश्न

प्रश्न 1:
प्रकाश-वैद्युत कार्य-फलन से क्या तात्पर्य है? (2009, 10, 11)
या
कार्य-फलन की परिभाषा लिखिए। (2013, 18)
या
कार्य-फलन से आप क्या समझते हैं? (2014)
उत्तर:
“वह न्यूनतम प्रकाश ऊर्जा जो किसी धातु पृष्ठ से इलेक्ट्रॉन उत्सर्जित करने के लिए आवश्यक होती है, उस धातु का प्रकाश वैद्युत कार्य-फलम (work function) कहलाता है। सामान्यत: इसको W से व्यक्त करते हैं।
W = hν0 अथवा w = hc/λ0

प्रश्न 2:
सीजियम का कार्यफलन 2eV है। इस कथन की व्याख्या कीजिए। (2010)
उत्तर:
सीजियम धातु के पृष्ठ से प्रकाश इलेक्ट्रॉन उत्सर्जित करने के लिए इस पर आपतित प्रकाश फोटॉन की न्यूनतम ऊर्जा 2 eV होनी चाहिए।

प्रश्न 3:
प्रकाश-वैद्युत प्रभाव में देहली आवृत्ति से क्या तात्पर्य है? इसकी क्या महत्ता है? (2011)
या
देहली आवृत्ति से आप क्या समझते हैं? (2013, 14, 17)
या
प्रकाश वैद्युत उत्सर्जन में देहली आवृत्ति से आप क्या समझते हैं? (2017)
उत्तर:
देहली आवृत्ति आपतित प्रकाश की वह न्यूनतम आवृत्ति है जो किसी धातु से प्रकाश-इलेक्ट्रॉन का। उत्सर्जन कर सके। इसे ν0 से प्रदर्शित करते हैं। इससे कम आवृत्ति के प्रकाश से धातु से कोई प्रकाश-इलेक्ट्रॉन नहीं निकलता है। यही इसकी महत्ता है।।

प्रश्न 4:
प्रकाश-वैद्युत प्रभाव में देहली तरंगदैर्ध्य से आप क्या समझते हैं? (2009, 17, 18)
उत्तर:
देहली तरंगदैर्ध्य-किसी धातु पर आपतित प्रकाश की तरंगदैर्घ्य का वह अधिकतम मान जिससे तरंगदैर्ध्य का प्रकाश धातु-पृष्ठ से प्रकाश इलेक्ट्रॉन उत्सर्जित कर सके, देहली तरंगदैर्ध्य कहलाता है। इसको λ0 से प्रदर्शित करते हैं। यह देहली आवृत्ति के संगत तरंगदैर्घ्य होती है, अर्थात् λ0= c/ν0, जहाँ c = प्रकाश की चाल (निर्वात् में)।

प्रश्न 5:
सीजियम धातु के पृष्ठ का कार्यफलन 1.8eV हो तो देहली तरंगदैर्ध्य क्या होगी? (2011,14)
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 6:
एक धातु का कार्य-फलन 2.5eV है, 2eV ऊर्जा के दो फोटॉन धातु पृष्ठ पर आपतित होते हैं। कारण सहित स्पष्ट कीजिए कि फोटो इलेक्ट्रॉन उत्सर्जित हींगे या नहीं। (2014)
उत्तर:
धातु का कार्य-फलन W = 2.5 eV है तथा इस पर आपतित दोनों फोटॉनों में प्रत्येक की ऊर्जा hν = 2 eV; चूँकि hν <W, अत: फोटो-इलेक्ट्रॉन उत्सर्जित नहीं होगा क्योंकि फोटो-इलेक्ट्रॉन का उत्सर्जन फोटॉन की ऊर्जा पर निर्भर करता है, धातु पर आपतित सभी फोटॉनों की कुल ऊर्जा पर नहीं।

प्रश्न 7:
किसी पृष्ठ का कार्य-फलन 2.5 इलेक्ट्रॉन वोल्ट है। उसके लिए देहली आवृत्ति ज्ञात कीजिए। (2013)
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 8:
किसी धातु जिसका कार्य-फलन 3.2eV है, पर 4.0 eV ऊर्जा वाला एक फोटॉन आपतित होता है। उत्सर्जित फोटो-इलेक्ट्रॉन की गतिज ऊर्जा कितनी होगी? (2013, 14)
उत्तर:
उत्सर्जित फोटो-इलेक्ट्रॉन की गतिज ऊर्जा
Ek = hν – W = 4eV- 3.2eV
= 0.8 eV= 0.8 x 1.6 x 10-19 जूल
= 1.28 x 10-19 जूल

प्रश्न 9:
किसी धातु के लिए कार्य फलन 3.3 इलेक्ट्रॉन वोल्ट है। धातु के लिए देहली आवृत्ति की  गणना कीजिए। (2017)
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 10:
प्रकाश-वैद्युत प्रभाव के प्रयोग में आपतित प्रकाश की आवृत्ति दोगुनी करने पर उत्सर्जित प्रकाश-इलेक्ट्रॉन की गतिज ऊर्जा कितनी बढ़ जायेगी ? (2012)
उत्तर:
∵ E = hν
∴ गतिज ऊर्जा दोगुनी हो जायेगी।

प्रश्न 11:
प्रकाश वैद्युत प्रभाव में आपतित प्रकाश की आवृत्ति और उत्सर्जित इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा के बीच ग्राफ खींचिए। (2017)
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 12:
फोटॉन की ऊर्जा तथा संवेग में सम्बन्ध लिखिए। (2009, 11)
उत्तर:
संवेग p =Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)(जहाँ E = ऊर्जा, c = प्रकाश का वेग)।

प्रश्न 13:
4000\mathring { A }  तरंगदैर्घ्य वाले एकवर्णीय प्रकाश के फोटॉन की ऊर्जा ज्ञात कीजिए। (2012)
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 14:
एक फोटॉन की ऊर्जा 30eV है। इसका संवेग ज्ञात कीजिए। (2012)
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 15:
डी-ब्रॉग्ली तरंगदैर्ध्य का सूत्र लिखिए। (2017)
उत्तर:
λ = Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)जहाँ, λ तरंगदैर्घ्य, h प्लांक नियतांक, m कण का द्रव्यमान तथा ν कण का वेग है।

प्रश्न 16:
एक इलेक्ट्रॉन 0.5 x 103 मी/से की चाल से गतिमान है। इससे सम्बद्ध डी-ब्रॉग्ली तरंगदैर्घ्य ज्ञात कीजिए। (2017)
उत्तर:
दिया है, ν = 0.5 x 103 मी/से, λ = ?
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 17:
एक गतिमान कण का डी-ब्रॉग्ली तरंगदैर्घ्य 2.0Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)  है। कण का संवेग क्या है? (2014, 17)
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 18:
किसी आवेशित कण का द्रव्यमान m तथा इस पर q आवेश है। यदि कण V विभवान्तर सेत्वरित किया जाए, तो इससे सम्बन्धित डी-ब्रॉग्ली तरं गदैर्घ्य का सूत्र लिखिए। (2015)

उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 19:
m द्रव्यमान के कण के साथ जुड़ी डी-ब्रॉग्ली तरंगदैर्घ्य λ  का सम्बन्ध इसके गतिज ऊर्जा K के पदों में लिखिए। (2016)
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
जहाँ λ = तरंगदैर्घ्य, m = कण का द्रव्यमान तथा K = गतिज ऊर्जा

प्रश्न 20:
प्रोटॉन तथा α-कण की डी-ब्रॉग्ली तरंगदैर्घ्य समान हों तो उनकी चालों में अनुपात क्या होगा? (mα = 4mp) (2016)
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

लघु उत्तरीय प्रश्न

प्रश्न 1:
प्रकाश-वैद्युत प्रभाव के नियम लिखिए। या प्रकाश-वैद्युत उत्सर्जन के नियम लिखिए। (2012, 15, 17)
उत्तर:
प्रकाश-वैद्युत प्रभाव के नियम: वैज्ञानिक लेनार्ड तथा मिलीकन ने प्रकाश-वैद्युत प्रभाव के सम्बन्ध में किये गये प्रयोगों से प्राप्त प्रेक्षणों के आधार पर कुछ नियम दिये जो प्रकाश-वैद्युत प्रभाव (ऊष्मा उत्सर्जन) के नियम कहलाते हैं।
प्रकाश-वैद्युत प्रभाव के नियम निम्नलिखित हैं

  1. किसी धातु की सतह से प्रकाश-इलेक्ट्रॉनों के उत्सर्जन की दर धातु की सतह पर गिरने वाले प्रकाश की तीव्रता के अनुक्रमानुपाती होती है।
  2. उत्सर्जित प्रकाश-इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा प्रकाश की तीव्रता पर निर्भर नहीं करती।
  3. प्रकाश-इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा प्रकाश की आवृत्ति के बढ़ने पर बढ़ती है।
  4. यदि आपतित प्रकाश की आवृत्ति एक न्यूनतम मान से कम है तो धातु से कोई भी प्रक़ाश-इलेक्ट्रॉन नहीं निकलता। यह न्यूनतम आवृत्ति (देहली आवृत्ति) भिन्न-भिन्न धातुओं के लिए भिन्न-भिन्न होती है।
  5. प्रकाश के धातु की सतह पर गिरते ही इलेक्ट्रॉन उत्सर्जित होने लगते हैं, अर्थात् प्रकाश के सतह पर गिरने तथा इलेक्ट्रॉन के सतह से बाहर निकलने के बीच कोई समय-पश्चता (time-lag) नहीं . होती, चाहे प्रकाश की तीव्रता कितनी भी क्यों न हो।

प्रश्न 2:
प्रकाश:वैद्युत धारा पर क्या प्रभाव पड़ता है, यदि (i) आपतित प्रकाश की तीव्रता बढ़ा दी जाए? (ii) आपतित प्रकाश की तरंगदैर्घ्य घटा दी जाए? (2013)
उत्तर:
(i) यदि आपतित प्रकाश की तीव्रता बढ़ा दी जाए तब धातु पर प्रति सेकण्ड अधिक फोटॉन गिरेंगे जिससे कि उत्सर्जित इलेक्ट्रॉनों की संख्या बढ़ेगी अर्थात् प्रकाश वैद्युत धारा बढ़ेगी।
(ii) आपतित प्रकाश की तरंगदैर्घ्य घटाने पर भी प्रकाश वैद्युत धारा को मान बढ़ जायेगा।

प्रश्न 3:
आइन्सटीन की प्रकाश-वैद्युत समीकरण लिखिए तथा इसकी व्याख्या कीजिए। (2009, 12, 15)
या
आइन्सटीन की प्रकाश-वैद्युत समीकरण लिखिए तथा इसकी सहायता से प्रकाश-वैद्युत प्रभाव के नियमों को समझाइए। (2017)
या
आइन्सटीन की प्रकाश-वैद्युत उत्सर्जन सम्बन्धी समीकरण के आधार पर प्रकाश-वैद्युत प्रभाव के नियमों की व्याख्या कीजिए। (2013)
या
आइन्सटीन का प्रकाश-वैद्युत प्रभाव का समीकरण लिखिए तथा प्रयुक्त संकेतों का अर्थ स्पष्ट कीजिए। (2014)
उत्तर:
आइन्सटीन की प्रकाश-वैद्युत समीकरण
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)mν2max = h(ν – ν0) ……..(1)
जहाँ m = इलेक्ट्रॉन का द्रव्यमान, νmax = उत्सर्जित फोटो इलेक्ट्रॉनों का अधिकतम वेग, h= प्लांक नियतांक, ν = धातु पर आपतित फोटॉन की आवृत्ति, ν0 = देहली आवृत्ति।
व्याख्या:
आइन्सटीन की प्रकाश-वैद्युत समीकरण के आधार पर प्रकाश-वैद्युत प्रभाव के नियमों की व्याख्या इस प्रकार की जा सकती है

(i) जब किसी धातु-पृष्ठ पर आपतित निश्चित आवृत्ति के प्रकाश की तीव्रता बढ़ायी जाती है तो सतह पर प्रति सेकण्ड आपतित फोटॉनों की संख्या उसी अनुपात में बढ़ जाती है परन्तु प्रत्येक फोटॉन की ऊर्जा hν नियत रहेगी। आपतित फोटॉन की संख्या बढ़ने से उत्सर्जित प्रकाश-इलेक्ट्रॉनों की संख्या बढ़ जाएगी, परन्तु समी० (1) से स्पष्ट है कि आवृत्ति के निश्चित होने तथा धातु विशेष के लिए ν0 निश्चित होने से पृष्ठ से उत्सर्जित सभी प्रकाश-इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा Ek एकसमान । होगी। अत: प्रकाश इलेक्ट्रॉनों के उत्सर्जन की दर तो आपतित प्रकाश की तीव्रता पर निर्भर करती है। परन्तु इनकी अधिकतम गतिज ऊर्जा नहीं। ये ही क्रमश: प्रकाश-वैद्युत प्रभाव के पहले तथा दूसरे नियम के कथन हैं।

(ii) समीकरण (1) से यह भी स्पष्ट है कि आपतित प्रकाश की आवृत्ति ν बढ़ाने पर उत्सर्जित प्रकाश-इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा Ek उसी अनुपात में बढ़ जाएगी। यही प्रकाश-वैद्युत प्रभाव के तीसरे नियम का कथन है।

(iii) समीकरण (1) में यदि ν < ν0 तो Ek का मान ऋणात्मक होगा, जो असम्भवं है। अतः इससे निष्कर्ष निकलता है कि यदि आपतित प्रकाश की आवृत्ति ν0 से कम है तो प्रकाश-इलेक्ट्रॉनों का उत्सर्जन सम्भव नहीं है, चाहे प्रकाश की तीव्रता कितनी भी अधिक क्यों न हो। यही प्रकाश-वैद्युत प्रभाव का चौथा नियम है।

(iv) जब प्रकाश किसी धातु-पृष्ठ पर गिरता है तो जैसे ही कोई एक प्रकाश फोटॉन धातु पर आपतित होता है, धातु का कोई एक इलेक्ट्रॉन तुरन्त उसे ज्यों-का-त्यों अवशोषित कर लेता है तथा धातु-पृष्ठ से उत्सर्जित हो जाता हैं। इस प्रकार धातु-पृष्ठ पर प्रकाश के आपतित होने तथा इससे प्रकाश-इलेक्ट्रॉन के उत्सर्जित होने में कोई पश्चता नहीं होती। यही प्रकाश-वैद्युत प्रभाव का पाँचवाँ नियम है।

प्रश्न 4:
विकिरण सम्बन्धी प्लांक की परिकल्पना समझाइए। इसके द्वारा फोटॉन के गतिमान द्रव्यमान का व्यंजक प्राप्त कीजिए। फोटॉन संवेग क्या होगा? या फोटॉन किसे कहते हैं ? इसके गतिज द्रव्यमान एवं संवेग का सूत्र लिखिए। (2012)
या
फोटॉन के गतिज द्रव्यमान का सूत्र लिखिए। (2012)
या
फोटॉन के विराम द्रव्यमान तथा गतिक द्रव्यमान से आप क्या समझते हैं? फोटॉन का संवेग P = \frac { h }{ \lambda }निगमित कीजिए जहाँ h प्लांक नियतांक तथा 2 फोटॉन की तरंगदैर्घ्य है। (2014)
उत्तर:
कृष्णिका विकिरण के स्पेक्ट्रमी वितरण की व्याख्या करने के लिए सन् 1900 में जर्मनी के वैज्ञानिक मैक्स प्लांक ने एक क्रान्तिकारी विचार रखा जिसे ‘प्लांक की क्वाण्टम परिकल्पना’ कहते हैं। इसके अनुसार, किसी पदार्थ द्वारा ऊर्जा का उत्सर्जन अथवा अवशोषण सतत रूप से न होकर ऊर्जा के छोटे-छोटे बण्डलों अथवा पैकेटों के रूप में होता है, जिन्हें ‘फोटॉन’ अथवा ‘क्वाण्टम’ कहते हैं। प्रत्येक तरंगदैर्घ्य 2 अथवा आवृत्ति (=c/λ) का अपना एक अलग फोटॉन होता है जिसकी ऊर्जा की मात्रा hν होती है; जहाँ । एक नियतांक है, जिसे ‘प्लांक नियतांक’ कहते हैं। प्लांक ने बताया कि कोई भी वस्तु ऊष्मा का उत्सर्जन अथवा अवशोषण इन फोटॉनों के पूर्ण गुणज के रूप में कर सकती है, अर्थात् कोई वस्तु hν, 2hν, 3haν,… आदि के रूप में ऊर्जा का अवशोषण अथवा उत्सर्जन करेगी।
प्लांक नियतांक का मात्रक जूल-सेकण्ड है।
प्लांक ने इस परिकल्पना के आधार पर ऊर्जा वितरण का सूत्र दिया जो कि ल्यूमर तथा प्रिंग्जहाइम के प्रायोगिक (Eλ – λ) वक्रों के पूर्णत: अनुकूल था। आइन्सटीन ने भी इस परिकल्पना की सहायता से प्रकाश-वैद्युत प्रभाव की सफल व्याख्या की।

फोटॉन का विराम द्रव्यमान तथा गतिक (गतिज) द्रव्यमान:
फोटॉन का विराम द्रव्यमान शून्य होता है, परन्तु इसका गतिक द्रव्यमान शून्य नहीं होता। फोटॉन प्रकाश की चाल से गति करते हैं तथा गतिज अवस्था में फोटॉन की ऊर्जा के कारण उसमें जो द्रव्यमान होता है, वह फोटॉन का गतिक द्रव्यमान । कहलाता है। आइन्सटीन के द्रव्यमान ऊर्जा समीकरण के अनुसार
फोटॉन की ऊर्जा E = mc2 …….(1)
जहाँ m = फोटॉन का गतिज द्रव्यमान
तथा c = फोटॉन (प्रकाश) का वेग
प्लांक के अनुसार फोटॉन की ऊर्जा E = hν …..(2)
समी० (1) व समी० (2) से, mc2 = hν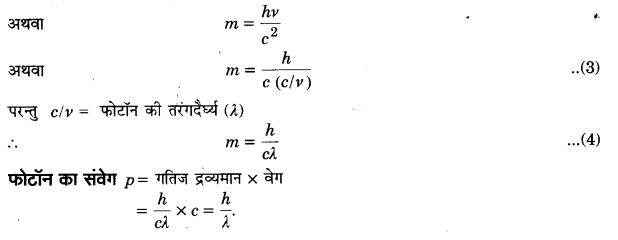
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 5:
द्रव्य तरंगें क्या हैं? द्रव्य तरंगों की तरंगदैर्ध्य का सूत्र लिखिए। (2017, 18)
या
लूईडी-ब्रॉग्ली के द्रव्य तरंग की अवधारणा स्पष्ट कीजिए। द्रव्य तरंगों के तरंगदैर्घ्य का सूत्र स्थापित कीजिए। (2009, 11, 16, 17)
या
डी-ब्रॉग्ली तरंगें क्या हैं? डी-ब्रॉग्ली तरंगदैर्घ्य के लिये व्यंजक लिखिए। (2010, 17)
या
m द्रव्यमान का एक कण वेग से गतिमान है। कण के साथ सम्बन्ध डी-ब्रॉग्ली तरंगदैर्घ्य का सूत्र लिखिए। (2012, 15)
या
द्रव्य तरंगें क्या हैं? डी-ब्रॉग्ली तरंगदैर्घ्य के लिए सूत्र लिखिए। इन तरंगों का प्रायोगिक सत्यापन करने वाले प्रयोग का नाम लिखिए। (2015)
या
डी-ब्रॉग्ली तरंगदैर्ध्य का व्यंजक लिखिए। (2016)
उत्तर:
द्रव्य तरंगें (Matter Waves)-सन् 1922 में डी-ब्रॉग्ली (de-Broglie) ने विचार रखा कि पदार्थ और विकिरण की पारस्परिक क्रिया समझने के लिए कणों को पृथक् रूप में न मानकर तरंग पद्धति से समन्वित माना जाये। उन्होंने बताया कि जब कोई द्रव्य-कण चलता है तो वह भी तरंग की भाँति व्यवहार करता है। इस सिद्धान्त का सत्यापन डेवीसन (Davission) और जर्मर (Germer) ने अपने प्रयोगों द्वारा किया। उन्होंने स्थापित किया कि इलेक्ट्रॉन के किरण पूँज का विवर्तन देखा जा सकता है, जो एक तरंग का गुण है। अत: द्वैती प्रकृति न केवल प्रकाश में होती है बल्कि यह द्रव्य-कणों में भी होती है।
अतः “गतिमान द्रव्य-कणों (इलेक्ट्रॉन, प्रोटॉन आदि) से तरंग सम्बद्ध होती है। इन तरंगों को द्रव्ये तरंगें अथवा डी-बॉग्ली तरंगें (de-Broglie’s Waves) कहते हैं। द्रव्य तरंगों की तरंगदैर्घ्य डी-ब्रॉग्ली तरंगदैर्ध्य कहलाती है।”
द्रव्य तरंगों की तरंगदैर्ध्य
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 6:
प्रकाश-वैद्युत प्रवाह पर एक प्रयोग में निम्न प्रेक्षण प्राप्त होते हैं
(i) आपतित प्रकाश की तरंगदैर्घ्य = 1.98 x 10-7 मीटर
(ii) संस्तब्ध विभव = 2.5 वोल्ट
फोटो इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा तथा धातु का कार्य फलन ज्ञात कीजिए। (2012)
उत्तर:
फोटो इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 7:
सोडियम का कार्य-फलन 2.0 eV है। ज्ञात कीजिए कि क्या 7000\mathring { A }तरंगदैर्घ्य का प्रकाश उसके | पृष्ठ से इलेक्ट्रॉन उत्सर्जित कर सकेगा? h = 6.6 x 10-34 जूल-से, c = 3 x 108 मी/से। (2009,11)
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
परन्तु यहाँ सोडियम का कार्य फलन W = 2.0 eV
चूंकि E < w
इसलिए 7000\mathring { A }तरंगदैर्घ्य का प्रकाश सोडियम के पृष्ठ से इलेक्ट्रॉन उत्सर्जित नहीं कर सकेगा।

प्रश्न 8:
एक पदार्थ से फोटो इलेक्ट्रॉन उत्सर्जन की देहली तरंगदैर्घ्य 6000Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)है। इसकी सतह पर 4000Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)तरंगदैर्घ्य का प्रकाश डाला जाता है। उत्सर्जित फोटो इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा तथा निरोधी-विभव ज्ञात कीजिए। (2012, 18)
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 9:
किसी धातु का कार्य-फलन 6.8 इलेक्ट्रॉन-वोल्ट है। इस पर 100\mathring { A }तरंगदैर्घ्य का विकिरण आपतित हो रहा है। उत्सर्जित फोटो-

उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 10:
5400\mathring { A }तरंगदैर्घ्य का विकिरण एक धातु पर गिरता है जिसका कार्य-फलन1.9 इलेक्ट्रॉन-वोल्ट है। उत्सर्जित फोटो-इलेक्ट्रॉन की ऊर्जा तथा उसका निरोधी विभव ज्ञात कीजिए। (2014)
उत्तर:
उत्सर्जित फोटो-इलेक्ट्रॉन की अधिकतम ऊर्जा
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 11:
एक प्रकाश सुग्राही धातु पृष्ठ का कार्य-फलन hν0 है। जब 2hν0 ऊर्जा के फोटॉन धातु पृष्ठ पर डाले जाते हैं तब 4×106 मीटर/सेकण्ड के अधिकतम वेग से इलेक्ट्रॉन उत्सर्जित होते हैं। यदि आपतित फोटॉन की ऊर्जा 5hν0 हो, तब उत्सर्जित इलेक्ट्रॉन का अधिकतम वेग क्या होगा? (2015)
उत्तर:
आइन्स्टीन का प्रकाश वैद्युत समीकरण
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 12:
300 वाट तथा 6000\mathring { A }तरंगदैर्घ्य के एकवर्षीय प्रकाश स्रोत से प्रति सेकण्ड कितने फोटॉन का उत्सर्जन होता है?
[प्लांक नियतांक (h) = 6.6 x 10-34 Js तथा प्रकाश की चाल (c) = 3×108 ms-1] (2017)
उत्तर:
प्रकाश स्रोत से उत्सर्जित प्रत्येक फोटॉन की ऊर्जा,
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
300 वाट के प्रकाश स्रोत से प्रति सेकण्ड उत्सर्जित ऊर्जा 300 जूल/सेकण्ड है।
अत: प्रकाश स्रोत से प्रति सेकण्ड निकलने वाले फोटॉन की संख्या
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 13:
1.6 x 10-27 किलोग्राम द्रव्यमान के न्यूट्रॉन की गतिज ऊर्जा 0.04 इलेक्ट्रॉन-वोल्ट है।  न्यूट्रॉन की डी-ब्रॉग्ली तरंगदैर्घ्य ज्ञात कीजिए। (2015)
उत्तर:
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

प्रश्न 14:
समान चाल से गतिशील इलेक्ट्रॉन एवं प्रोटॉन से सम्बद्ध डी-ब्रॉग्ली तरंगदैर्घ्य का अनुपात ज्ञात कीजिए। प्रोटॉन का द्रव्यमान इलेक्ट्रॉन के द्रव्यमान का 1840 गुना है। (2016)
उत्तर:
हम जानते हैं कि ν  चाल से गतिमान m द्रव्यमान के कण से बद्ध डी-ब्रॉग्ली तरंगदैर्घ्य,  λ =  Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)
जहाँ h प्लांक नियतांक है, इस प्रकार
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)

दीर्घ उत्तरीय प्रश्न

प्रश्न 1:
प्रकाश-वैद्युत उत्सर्जन सम्बन्धी आइन्स्टीन की समीकरण  Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)mν2max = h(ν – ν0) की स्थापना कीजिए। (2010, 14, 16, 17)
या
क्वाण्टम मॉडल के आधार पर प्रकाश-वैद्युत प्रभाव की व्याख्या कीजिए तथा आइन्स्टीन के प्रकाश-वैद्युत समीकरण को व्युत्पादित कीजिए। (2011, 15)
या
प्रकाश-वैद्युत प्रभाव से आप क्या समझते हैं? आइन्स्टीन के प्रकाश-वैद्युत समीकरण को व्युत्पन्न कीजिए। (2012)
या
आइन्सटीन द्वारा प्रकाश वैद्युत उत्सर्जन की घटना की व्याख्या कीजिए तथा प्रकाश-वैद्युत समीकरण व्युत्पादित कीजिए। (2013)
या
प्रकाश-वैद्युत उत्सर्जन सम्बन्धी आइन्स्टीन की समीकरण को व्युत्पन्न कीजिए। (2013, 17)
या
प्रकाश वैद्युत उत्सर्जन में उत्सर्जित फोटो-इलेक्ट्रॉनों की अधिकतम ऊर्जा का समीकरण व्युत्पन्न कीजिए। (2015, 17)
उत्तर:
प्रकाश-वैद्युत प्रभाव (Photoelectric Effect)-जब किसी धातु पर उच्च आवृत्ति का प्रकाश (जैसे—पराबैंगनी विकिरण) डाला जाता है तो उसकी सतह से इलेक्ट्रॉन निकलने लगते हैं।
” धातुओं पर प्रकाश के आपतित होने से उनकी सतह से इलेक्ट्रॉनों के उत्सर्जन (emission) की घटना को प्रकाश-वैद्युत प्रभाव (photoelectric effect) कहते हैं।”
प्रकाश-वैद्युत प्रभाव की घटना में उत्सर्जित इलेक्ट्रॉनों को प्रकाश-इलेक्ट्रॉन अथवा फोटो- इलेक्ट्रॉन (photoelectron) तथा इन इलेक्ट्रॉनों के प्रवाह के कारण उत्पन्न वैद्युत धारा को प्रकाश-वैद्युत धारा (photoelectric current) कहते हैं।

आइन्सटीन की प्रकाश-वैद्युत समीकरण (Einstien’s Photoelectric Equation):
वैज्ञानिक आइन्सटीन ने प्रकाश-वैद्युत प्रभाव की व्याख्या प्रकाश के क्वाण्टम मॉडल के आधार पर इस प्रकार दी। जब कोई फोटॉन धातु की प्लेट पर गिरता है तो वह अपनी ‘संमस्त ऊर्जा’ धातु के भीतर उपस्थित इलेक्ट्रॉनों में से किसी एक ही इलेक्ट्रॉन को स्थानान्तरित (transfer) कर देता है तथा ऊर्जा का कुछ भाग इलेक्ट्रॉन को धातु के अन्दर से बाहर निकालने में व्यय हो जाता है जो धातु का कार्य-फलन कहलाता है। तथा शेष ऊर्जा उत्सर्जित इलेक्ट्रॉन को उसकी गतिज ऊर्जा के रूप में प्राप्त हो जाती है जिससे इलेक्ट्रॉन धातु पृष्ठ से उत्सर्जित हो जाता है। यही प्रकाश-वैद्युत प्रभाव है। चूंकि सभी इलेक्ट्रॉन धातु की सतह से ही उत्सर्जित नहीं होते; अतः धातु से विभिन्न ऊर्जाओं के इलेक्ट्रॉन उत्सर्जित होते हैं; क्योंकि जो इलेक्ट्रॉन धातु के भीतर से निकलकर सतह पर पहुँचते हैं वे सतह तक आने में धन आयनों व परमाणुओं से टकराते हैं; जिससे वे कुछ ऊर्जा खो देते हैं। अतः जो इलेक्ट्रॉन धातु की सतह से उत्सर्जित होते हैं, उनकी गतिज ऊर्जा अपेक्षाकृत अधिक होती है; क्योंकि उनकी ऊर्जा टकराने में नष्ट नहीं होती है। इस प्रकार धातु की ऊपरी सतह से उत्सर्जित प्रकाश इलेक्ट्रॉन की गतिज ऊर्जा अधिकतम होती है। माना किसी धातु की सतह से उत्सर्जित किसी प्रकाश इलेक्ट्रॉन की अधिकतम गतिज ऊर्जा E, तथा इसको धातु के अन्दर से बाहर सतह पर निकालने के लिए आवश्यक ऊर्जा w है। यहाँ w धातु का कार्य-फलन होगा। अतः आइन्सटीन द्वारा दी गयी प्रकाश-वैद्युत उत्सर्जन की उपर्युक्त व्याख्या के अनुसार इन दोनों प्रकार की ऊर्जाओं का योग ही धातु के अन्दर सतह के निकट इलेक्ट्रॉन द्वारा अवशोषित फोटॉन की ऊर्जा hay के बराबर होगा।
∴ Ek + W= hν
अथवा  Ek =  hν – W   …….(1)
समीकरण (1) से स्पष्ट है कि यदि प्रकाश फोटॉन की ऊर्जा hν कार्य-फलन W के बराबर है तो धातु की सतह से कोई भी इलेक्ट्रॉन नहीं निकलेगा। यदि दी हुई धातु के लिए देहली आवृत्ति ν0 है तो इस आवृत्ति का फोटॉन, इलेक्ट्रॉन को धातु की सतह तक लाने में ही समर्थ होगा, क्योंकि ऐसे फोटॉन की ऊर्जा hν0 इलेक्ट्रॉन को धातु की सतह तक लाने में ही व्यय हो जाएगी। अत: सतह पर इसका वेग शून्य होगा, अर्थात् इस फोटॉन की ऊर्जा hν0 धातु के कार्य-फलन के बराबर होगी। अतः W = hν0
w का मान समी० (1) में रखने पर
Ek = hν – hν0
अथवा E = h(ν- ν0) …….(2)
यदि धातु की सतह पर निकलने वाले इलेक्ट्रॉन का अधिकतम वेग νmax है, तो इसकी अधिकतम गतिज ऊर्जा Ek = Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)mν2max = h(ν – ν0) होगी। Ek का यह मान उपर्युक्त समी० (2) में रखने पर
Solutions Class 12 भौतिकी विज्ञान-II Chapter-3 (विकिरण तथा द्रव्य की द्वैत प्रकृति)mν2max = h(ν – ν0)
इस समीकरण को ‘आइन्सटीन की प्रकाश-वैद्युत समीकरण’ (Einstien’s photoelectric equation) कहते हैं।


एनसीईआरटी सोलूशन्स क्लास 12 भौतिकी विज्ञान-II

Tags: